4th Class Mathematics Area, Perimeter and Volume Area

     Area

Look at the following pictures:

Shaded part in the figures given above represents area. So area is a mathematical term which tell us how much surface a particular object requires to be placed. Thus, we can say that area is the amount of surface which a particular object occupies.

Let us study about the area of some geometrical figures.  

Area of a Triangle

Area of a triangle is half of the product of the base and corresponding height. So to find the area of a triangle we multiply the base and corresponding height of the triangle and then divide the product by 2.

Thus Area of a triangle\[=\frac{1}{2}\times \text{Base}\times \text{Height}\]

Area of the triangle \[\text{ABC}=\frac{1}{2}\times \text{AD}\times \text{BC}\]

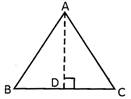
Height

In a triangle, the length of the line segment which joins one vertex to the opposite side (on extending or without extending) making the angle of 90° is called height of the triangle.

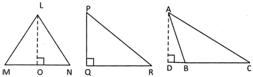
LO, PQ and AD are heights of the triangles \[\Delta \text{LMN},\Delta \text{PQR}\] and\[\Delta \text{ABC}\]respectively.  

Base

Base is the side of the triangle to which height is drawn.

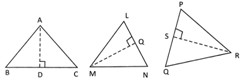
BC, LN and PQ are the bases of the triangles \[\Delta \text{ABC},\text{ }\Delta \text{LMN},\]and\[\Delta \text{PQR}\]respectively.  

Find the area of the triangle ABC as shown in the following figure.

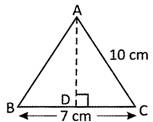
Solution:

Area of the triangle\[\text{ABC}=\frac{1}{2}\times \text{Base}\times \text{Height}\] \[=\frac{1}{2}\times \text{BC}\times \text{AD}=\frac{1}{2}\times \text{7cm}\times \text{1}0\text{ cm}=\text{35 c}{{\text{m}}^{\text{2}}}\].  

Area of a Rectangle

Area of a rectangle is equal to the product of its length and breadth. So to find the area of the rectangle we multiply the length of the rectangle by breadth of the rectangle. Thus area of a rectangle\[=\text{Length}\times \text{Breadth}\]

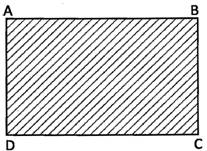
Area of the rectangle\[~\text{ABCD}=\text{AB}\times \text{BC}\]  

Length

The longer side of a rectangle is called length of the rectangle.

Look at the following figure:

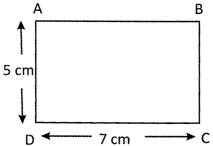
AB or CD is the length of the rectangle ABCD  

  Breadth

The smaller side of a rectangle is called breadth of the rectangle.  

Look at the following figure:

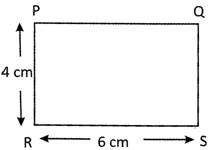
PR or QS is the breadth of the rectangle PQRS.  

Find the area of the given rectangle.

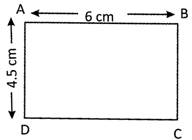
Solution:

In rectangle ABCD, length AB = 6 cm and breadth BC = 4.5 cm

Thus area of the rectangle\[\text{ABCD}=\text{AB}\times \text{BC}=\text{6}\]\[\text{cm}\times \text{4}.\text{5cm}=\text{27c}{{\text{m}}^{\text{2}}}\]  

Area of a Square

We know that all the squares are also rectangles and area of a rectangle is found by multiplying the corresponding sides (length and breadth) of the rectangle. In a square, all the sides are equal so area of the square is equal to the product of any two sides. So to find the area of a square we multiply length of any two sides of the square. Thus, area of a square\[=\text{Side}\times \text{Side}=\text{Sid}{{\text{e}}^{\text{2}}}\]

Area of the square \[\text{ABCD}=\text{AB}\times \text{AB}=\text{A}{{\text{B}}^{\text{2}}}\]  

Find the area of the following square.

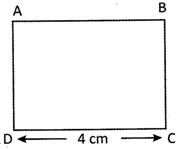
Solution:

ABCD is a square

\[\text{AB}=\text{BC}=\text{CD}=\text{DA}=\text{4 cm}\]

Area of the square\[\text{ABCD}=\text{Side}\times \text{Side}=\text{4cm}\times \]\[\text{4 cm}=\text{16 c}{{\text{m}}^{\text{2}}}\]  

  Area of a Circle

To find the area of a circle, square of the radius is multiplied by a constant (constant is a value which does not change). Symbol of the constant is\[\pi \]whose value is\[\frac{22}{7}\]

Thus, area of the circle\[=~\pi \times \text{radiu}{{\text{s}}^{\text{2}}}\]

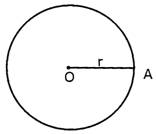
Or Area of the circle\[=~\pi {{r}^{\text{2}}}\]  

Find the area of the following circle:

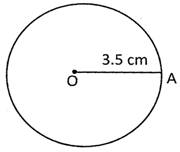
Solution:

Area of the circle\[=~\pi {{r}^{\text{2}}}\]

\[=\frac{22}{7}\times \text{3}.\text{5 cm}\times \text{3}.\text{5 cm}=\text{33}.\text{5 c}{{\text{m}}^{\text{2}}}\]