5th Class Mathematics Area, Perimeter and Volume Perimeter

   Perimeter

 

 

As we know all the geometrical shapes like triangles, quadrilaterals, etc. occupy some area. Perimeter is referred as the length of the boundary line which surrounds the area occupied by a geometrical shape. In the rectilinear figures the line segment which bounds the area are called sides. Thus we can say perimeter of a geometrical shape is the sum of the length of the all sides which bound the area occupied by that shape.  

 

 

Find the perimeter of the following figure:

 

 

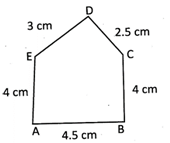
Explanation

Perimetre of the figure \[=AB+BC+CD+DE+EA\]

Perimetre of the figure \[=4.5cm+4cm+2.5cm+3cm+4cm=18cm.\]  

 

 

Perimeter of the Triangles

A triangles has three sides.

 

 

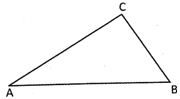
Perimetre of the triangle \[\text{ABC=AB+BC+CA}\]

Thus, perimetre of a triangle is the sum of length of its three sides.  

 

 

Find the perimetre of the following triangle:

 

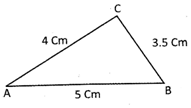
Perimetre of the triangle \[~ABC=AB+BC+AC\] \[=4\text{ }cm+3.5\text{ }cm+5cm\] \[=12.5\text{ }cm.\]  

 

 

Perimetre of an Equilateral Triangle

Perimetre of an equilateral triangle is equal to \[3\times \]side.

 

 

Perimetre of the triangle \[~ABC=AB+BC+CA\]                

In an equilateral triangle all sides are equal Therefore,\[~AB=BC=CA\]

Thus perimetre of the equilateral triangle \[ABC=AB+AB+AB\] \[=3\times AB\]

AB is a side of the equilateral triangle ABC.

Therefore, perimetre of an equilateral triangle \[=3\times \]side.  

 

 

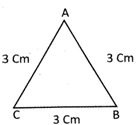
Find the perimetre of the following triangle:

 

               

 

Explanation

Perimetre of an equilateral triangle \[=3\times \]side In the triangle ABC Perimetre of the triangle\[~ABC=3\times AB\] \[\therefore AB=BC=CA=4cm\] Therefore, perimetre of the triangle ABC \[=3\times 4\,cm\] =12 cm.  

 

 

Perimetre of Isosceles Triangle

 

 

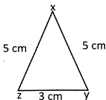
Perimetre of the triangle \[XYZ=XY+YZ+ZX\]

An isosceles triangle has two equal sides In the triangle \[XYZ,\] \[XY=XZ\]

Thus perimetre of\[~XYZ=XY+XY+ZX\] \[=2\times XY+YZ\] Here \[XY\] is one of the equal sides. Therefore, perimetre of an isosceles triangle \[=2\times \]length of one of the equalsides + length of the unequal side.  

 

 

Find the perimetre of the following triangle:

 

Explanation

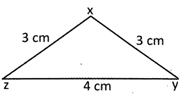
Perimetre of an isosceles triangle \[=2\times \]one of the equal sides + unequal side In the triangle \[XYZ\] .            

Perimetre of the triangle \[XYZ\text{ }=2\times XY+YZ\] \[XY=ZX=3\text{ }cm\]and\[YZ=4cm\] therefore,

perimetre of the triangle \[~XYZ=2\times 3\text{ }cm+4\text{ }cm\] \[=10\text{ }cm.\]  

 

 

Perimetre of Scalene Triangles

 

 

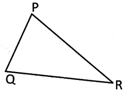
Perimetre of the triangle \[~PQR=PQ+QR+RP\]

All the sides of an scalene triangle are of different lengths Therefore, perimetre of the triangle \[PQR=PQ+QR+PR\] Thus perimetre of an scalene triangle = Sum of the length of all three sides.  

 

 

Find the perimetre of the following triangle:

Explanation

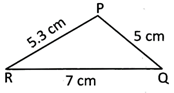
Perimetre of an scalene triangle = Sum of the length of all sides In triangle PQR

Perimetre of the triangle PQR = PQ + QR + RP PQ = 5 cm, QR = 5.3 cm, and RP = 7 cm

Therefore, perimetre of the triangle PQR = 5 cm + 5.3 cm + 7 cm = 17.3 cm.    

 

 

Perimetre of the Quadrilateral

A quadrilateral has four sides.

 

 

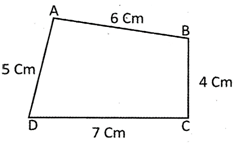
In quadrilateral ABCD, perimetre = AB + BC + CD + DA

Thus perimetre of a quadrilateral is the sum of length of its all four sides.  

 

 

Find the perimetre of the following quadrilateral:

 

 

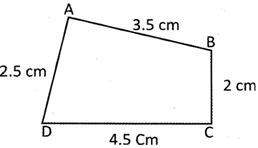
Explanation

Perimetre of the quadrilateral ABCD = AB + BC + CD + DA = 22 cm = 3.5 cm + 2 cm + 4.5 cm + 2.5 cm = 12.5 cm.  

 

 

Perimetre of Rectangles 

 

        

 

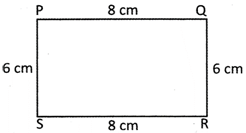
In the given rectangle PQRS

Perimetre of the rectangle PQRS = PQ + QR + RS + PS

We know that opposite sides of a rectangle are equal

Therefore, PQ = RS

And QR = PS

Thus perimetre of the rectangle

PQRS = PQ + QR + PQ + QR

= PQ + PQ + QR + QR

= 2 x PQ + 2 x QR                

= 2(PQ+QR)

PQ is the length of the rectangle and QR is the breadth of the rectangle

Thus perimetre of a rectangle = 2 (Length + Breadth).  

 

 

Find the perimetre of the following rectangle:

 

 

Explanation

Perimetre of the rectangle ABCD = 2(Length + Breadth)

=2(AB+BC)

= 2 (8 cm + 6 cm) = 28 cm.              

 

 

Perimetre of Squares

 

 

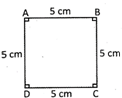
Perimetre of the square ABCD = AB + BC + CD + DA

We know that all sides of a square are equal AB = BC = CD = DA

Therefore, perimetre of the square ABCD = AB + AB + AB + AB =4AB

AB is a side of the square

Thus perimetre of a square \[=4\times \]side.  

 

 

Find the perimetre of the square whose length of one side is 7 cm.

 

Solution:

Perimetre of a square = 4 x side

\[=\text{ }4\times 7\text{ }cm=28\text{ }cm\]  

 

 

Perimetre of a Circle

 

 

Circle is made up of a curved line. To find the length of that curved line we multiplythe diameter of the circle by a constant ?\[\pi \]?. Value of \[\pi \](pie) is \[\frac{22}{7}\]

Thus, Perimetre of a circle \[=\pi \times \] Diametre

Or Perimetre of a circle \[=\pi \times 2\times \]Radius (Diametre = 2 xradius)

Perimetre of the circle \[=\pi d\]

Or Perimetre of the circle \[=2\pi r\]  

 

 

If radius of a circle is 3.5 cm, find the perimetre of the circle.

 

Solution:

Perimetre the circle \[2\pi r\] 22

\[=2\times \frac{22}{7}\times 3.5=22\,cm\]