5th Class Mathematics Factors and Multiples Factors and Multiples

LEARNING OBJECTIVES

This lesson will help you to:

• recognize and learn factors and multiples.
• understand how to find factors and multiples.
• understand the real life applications of factors andmultiples.
• understand and draw factor trees.
• find common factors and multiples of two numbers.

 

Real - Life Example

• We are surrounded by numbers in each & every sphere of our life. Factors & multiples are also commonly used in our everyday lives. We use factors when we want to arrange things in different ways. For example, arranging books in rows & columns, making groups of children in different ways etc.

 

QUICK CONCEPT REVIEW

FACTORS

It was picture day in Ria's school. Her teacher made all the students stand in a single line. But all of them couldnot come in the frame.

 

 

 

This way also all the students were not fitting in the frame.

Then she made 4 lines of 5 each. Now all the students could fit in the frame.

So here we saw three different ways to make 20 students stand in lines.                                      

The first way is \[1\times 20\]

The second way is \[2\times 10\]

& the third way is \[5\times 4\]

Therefore, we can say that 1,20,2, 5 & 4 are the factors of 20.

Definition of factors: The factors of a number are thosewhich divide the number without leaving any remainder.

Thus, factors of a number divide the number completely,

Note: A number can have many factors.        

• Prime factors: Factors of a number which areprime are called its prime factors.
• Prime factorization: A factosation in whichevery factor is prime is called prime factorization of the number.
• Co-prime: Two numbers are co-prime if they haveonly 1 as the common factor.

 

FACTOR TREE:

• A Factor Tree is a diagram which is used to break down a number by dividing it by its factors until all the numbers.
• We can make different factor tress of a same number.

Example 1: A factor tree of 8 is given in figure A. Here 8 has been broken into 2 factors 4 A 2. But 4 is not a prime number. 4 is again broken into 2 factors 2 & 2 as shown in

 

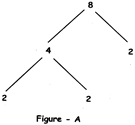
figure - A. Therefore, the factors of 8 are 2, 2 A 2.

Example 2: We can make factor trees of a same number 60 in different ways as shown in figures - B, C and D:

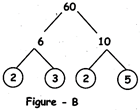
Fig.-B: This is a factor tree of 60. Here 60 has been broken into two factors 6 & 10. But 6 & 10 are not prime numbers. 6 & 10 are again broken into two factors each. 6 is broken in 2 & 3 and 10 is broken into 2 & 5.

 

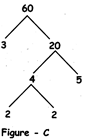
Fig.-C: This is also the factor tree of 60. Here 60 has been broken into 3 & 20. 20 is further broken into 4 & 5. Again 1 more branch is added to thisfactor tree by breaking 4 into 2 & 2.

 

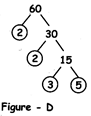
Fig. D: This is another factor tree for 60. Here 60 has been broken into 2 & 30. 2 is a prime number hence we will leave it as it is and further break30 into two factors 2 & 15.15 is again broken intotwo factors 3 & 5. Now 3 & 5 are prime numbers,therefore, the tree is complete now. That is, we cannot add any more branch to it.

 

COHHON FACTORS

The same factors of two or more than two differentnumbers are called common factors.

Let us find out the factors of 15& 21.

Factors of 15 are 1, 3, 5 & 15.

Factors of 21 are 1, 3, 7 & 21.

Therefore, Common factors of 15 & 21 are 1 and 3.

HIGHEST COMMON FACTOR (H.C.F) OR GREATEST COMMON FACTOR (G.C.F.)

The common factor which is highest among the commonfactors of two or more than two numbers is called H.C.F.of that numbers.

 

Methods to find H.C.F. :

(i)    By listing factors:

Factors of 12 = 1. 2. 3. 4. 6, 12

Factors of 32 = 1. 2.4. 8,16, 32

Common factors of 12 and 32 = 1.2,4

H.C.F. of 12 and 32 = 4

(ii)   Division Method: This method is useful to find the H.C.F. of greater numbers. This method involves the following steps:

• The greater number is divided by the smaller number.
• The remainder left after subtraction is taken as divisor and divisor as dividend for the nextstep of division.
• The process is repeated unless remainder becomes 0.

(d)  The last divisor is the H.C.F.

 

Example: Find the HCF of 762 and 1270.

Sol.               

 

   

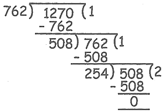
So, HCF of 762 and 1270 is 254.

(iii)    By prime factorization method:

H.C.F. of 12 and 24

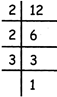
\[12=2\times 2\times 3\]

\[24=2\times 2\times 2\times 3\]

Common prime factors \[=2\times 2\times 3=12.\]

So. H.C.F of 12 and 24 = 12.

 

MULTIPLES

It is Diwali night, Pinki & her family are celebrating & enjoying together. Pinki saw the lightning’s all around.

She saw many colorful lights. She started counting thenumber of bulbs.

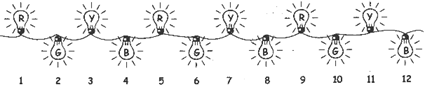
She saw that blue bulbs are placed at 4th place, 8th place, and 12th place and so on.....

Let us observe these numbers. 4, 8, 12......

This is similar to the table of 4 or we can say that thesenumbers are the multiples of 4. Can you tell the nextmultiple of 4?

 

DEFINITIION OF MULTIPLES

• A multiple is a number that is the product of a givennumber and some other number.

For example: If A x B = C, C is multiple of both Aand B.

• A multiple is basically a time table.
• We can find the multiple of a number by multiplyingit by 1,2,3,4, and so on.

 

COMMON MULTIPLES

For Example, let us find out the multiples of 3 & 5.

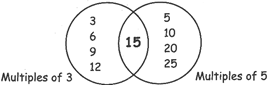
Multiples of 3: 3, 6, 9,12,15,18, 21, 24....

Multiples of 5: 5,10,15, 20, 25.......

Therefore, the common multiple of 3 <& 5 is 15.

 

Least Common Multiple (L.C.M.)

The least common multiple among the common multiples of two or more than two numbers is called their L.C.M.

 

Methods to find L.C.M.

(i)   Listing multiples and then finding out the least common multiple.

Example : Multiples of 5 = 5,10,15, 20, 25, 30, 35, 40, ———

Multiples of 7 = 7, 14, 21, 28, 35,42, -——

Common multiples of 5 and 7 = 35, 70, ----

Least common multiple of 5 and 7 = 35.

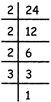
(ii)   Prime factorization method (Division method)

Now, \[2\times 2\times 3\times 3\times 2=72\]

Hence, L.C.M. of 36 and 72 = 72.

Relationship between L.C.M. and H.C.F.

\[L.C.M\times H.C.F.=\]Product of the two numbers.

 

Rules of Divisibility

1. A number is divisible by 2 if it has 0 or an evennumber in its ones place.
2. A number is divisible by 3 if the sum of its digits isdivisible by 3.
3. A number is divisible by 4 if the number formed bythe tens and ones digits is divisible by 4.
4. A number is divisible by 5 if it has 0 or 5 in its onesplace.
5. A number is divisible by 10 if it has 0 in its onesplace.
6. A number is divisible by 9 if the sum of its digits isdivisible by 9.
7. A number is divisible by 15 if it is divisible by both3 and 5.

Note: If a number is divisible by another number, it isalso divisible by each factor of that number.

 

Amazing Facts

• Every number is the greatest factor of itself.
• 1 is the factor of every number.
• The factors of a number by another and there is no remainder, the divisor & the quotient are the factors of the first number.
• If we divide by 1 number by another and there is no remainder, the divisor & the quotient are the factors of the first number.
• Every number except 1 has at least 2 factors. That is 1 & the number itself.
• A number is a multiple of itself.
• Every number is a multiple of 1.
• Every multiple of a number is greater than or equal to the number itself.
• There is no end to the multiple we can get of a particular number