Fractions and Operation on Fractions
Category : 5th Class
LEARNING OBJECTIVES
This lesson will help you to:
Real – Life Example
QUICK CONCEPT REVIEW
\[\frac{\text{Numeratar}}{\text{Denominatar}}\]
Where the
Numerator = Number of parts chosen
And the
Denominator = Total number of the parts
Amazing Fact
Here is Pi written to 50 decimal
Places: 3.1415926535897932384624338327950288419716939937510
Example: Fraction 1/3 is shown by the pie chart below. The pie is divided into 3 equal parts. The green part is equal to one third of the pie, thus 1/3.
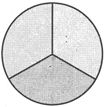
Part of a whole
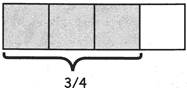
√ the top number (the numerator) says how many parts the whole is divided into.
√ the bottom number (the denominator) says how many you have.
Comparing fractions: Fractions are compared to see if one fraction is equal to (=), greater than (>) or smaller than (<) the other fraction.
Steps to compare two fractions :
Step 1: Find a common denominator by taking L.C.M of all different denominators.
Step 2: Make equivalent fractions with the new denominator.
Step 3: Compare the numerators.
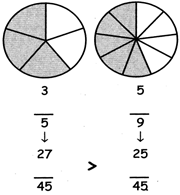
Example: Compare the fractions 3/5 and 7/9.
Step 1: L.C.M of 5 and 9 =45
Step 2: \[\text{3/5=}\frac{\text{3}}{\text{5}}\text{ }\!\!\times\!\!\text{ }\frac{\text{9}}{\text{9}}\text{=27/45;7/9=}\frac{\text{7 }\!\!\times\!\!\text{ 5}}{\text{9 }\!\!\times\!\!\text{ 5}}\text{=35/45}\]
Step 3: Since 27 < 35 so 3/5 < 7/9.
Note: If the numerator is same, the fraction with greater denominator is smaller.
Shortcut Method: To compare the two fractions, simplify cross multiply them.
Historical preview
Equivalent Fraction: To find equivalent fractions, multiply the numerator and denominator by the same number (except zero).
Equivalent fractions may look different, but they have the same value.
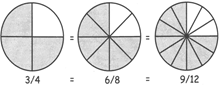
The fractions three-fourths, six-eighths, and nine- twelfths are equivalent.
Estimating the degree of closeness of a fraction
Example: 2/5, 5/26, 8/15 etc.
Example: 3/14, 4/17, 7/26 etc.
Decimal Fractions
Decimal fraction is a fraction with denominator 10,100, 1000 etc. For example fractions 1/10, 1/100, 1/1000 can be written as 0.1, 0.01, 0.001 respectively. 0.1, 0.01, 0.001 are decimal fractions.
Each decimal fraction has two parts- a whole number and a decimal. The point or dot that separates both the parts is called a decimal point. The number of digits in the decimal part gives the number of decimal places.
Example: 234.5623
In this number 234 is a whole number and 5623 is a decimal number.
This number has 4 decimal places.
Example 1: A log of wood of length 5 m is given below. It is to be cut into 10 equal parts.
![]()
The length of each part represents 1/10 of the length of the whole wood.
So, the length of each part of a 5m long log of wood is 5m x 1/10 = 5/10 m. 5/l0 m can also be written as 0.5.
Misconcept/ concept
Misconcept : The common misconception is that decimals and fractio9ns are defferent types of numbers. Hence there is no equivalent fraction for any decimal.
Concept : Taking an example of a decimal 4.422 which is to be converted to its equivalent fraction. Now this decimal can be expressed as 4 and the fraction 422/1000 or 4422/1000. These are fraction equivalent. These can be simplified by dividing both numerator and deno0minator by 2 to give 4.422 = 2211/500 or 4(211/500).
Misconnect: The value of A \[\div \] 1/B is equivalent to A \[\div \] B and hence has value A/B. Taking an example, the value of 3 \[\div \] ¼ is equivalent to 3 \[\div \] 4 and hence has ¾ or 0.75.
Example 2: Rs. 5 is to distributed equally among 10 students.
So, Rs. 5 is to be divided into 10 equal parts i.e. each student gets Rs. 5/10 or Rs. 0.50.
Expressing a decimal as a fraction and vice-versa
Decimal into Fraction
Write the decimal as the numerator without the decimal point and then write the denominator as 1 followed by as many zeroes as there are decimal places in the decimal.
Example: 0.8 = 8/10, 0.25 = 25/100, 0.2147 = 2147/10000 etc.
Fraction into Decimal
The fractions having denominators 10, 100 or 1000 can easily be converted into decimals. Place the decimal point from right to left in the numerator after as many digits as there are zeroes in the denominator.
Example: 5/100 = 0.05, 4/1000 = 0.004, 3/10 = 0.3 etc.
The fractions with denominators other than 10,100 or 1000 can also be converted to decimals by first converting 1 their denominators to 10,100 or 1000 and then following the same steps as above.
Example: 1/5 = 1/5 x 2/2 = 2/10 = 0.2.
More about Fractions:
Equivalent Fractions: Fractions having the same value, 1 even though they may look different.
Example: \[\frac{1}{2}\] and 2/4 both has the same value because they both are "half" Like Fractions: Fractions having the same denominator.
Example: \[\frac{1}{2}\] and 3/2 are like fractions having the same denominator as 2.
While comparing the fractions, if the fractions are like fractions, the fraction with bigger numerator is greater.
If the fractions are not like fractions, convert fractions into like fraction using the LCM of the denominator and then compare.
Important points
These conversions must be kept in mind when dealing with decimal fractions.
1 meter = 100 centimeter
1 kilometer = 1000 meter
1 rupee = 100 paise
You need to login to perform this action.
You will be redirected in
3 sec
