Angle
Category : 5th Class
Inclination between two rays having common end point is called angle.
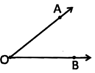
In the above given picture, OA and OB are two rays which have a common end point 0. Point 0 is called vertex and rays OA and OB are called arms. The inclination between the rays OA and OB is called angle AOB, and it is denoted as \[\angle \text{AOB}\text{.}\]

Angle is measured in degree. Symbol of the degree is \[~{{''}^{o}}''\] and written as \[{{a}^{o}}.\]
![]() Types of Angle
Types of Angle
There are different types of angles.
(a) Acute angle
(b) Right Angle
(c) Obtuse angle
(d) Straight angle
![]() Acute Angle
Acute Angle
An angle which measures between 0° and 90° is called acute angle.

![]()
Measure the given below angle and find is it an acute angle.
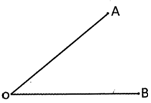
Explanation
Measure of the above given angle is \[{{40}^{o}}.\]
Therefore, the angle is an acute angle
![]() Right Angle
Right Angle
An angle of \[{{90}^{o}}\] is called right angle.

![]() Obtuse Angle
Obtuse Angle
An angle which measures between \[{{90}^{o}}\] and \[{{180}^{o}}\] is called obtuse angle.

![]() Straight Angle
Straight Angle
An angle which measures \[{{180}^{o}}\] is called straight angle.
![]()
![]() Triangle
Triangle
The geometrical shapes having three sides are called triangle.
![]() Properties of Triangle
Properties of Triangle
Triangle has:
(i) Three sides,
(ii) Three angles
(iii) Three vertices
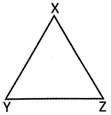
Three sides of the triangle \[\text{XYZ}\]are\[\text{ }\!\!~\!\!\text{ XY, YZ,}\] and \[\text{ZX}\]
Three angles of the triangle are \[\angle \text{X,}\angle \text{Y,}\]and \[\angle Z\]
Three vertices of the triangle are point \[\text{X,}\] point Y, and point Z.
![]() Types of Triangle
Types of Triangle
Triangle has been classified:
(a) On the basis of sides
(b) On the basis of angles
![]() Sides Based Classification
Sides Based Classification
On the basis of sides, triangles are of three types
(i) Equilateral Triangle
(ii) Isosceles Triangle
(iii) Scalene Triangle
![]() Equilateral Triangle
Equilateral Triangle
A triangle whose all sides are of equal length is called equilateral triangle.
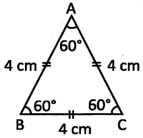
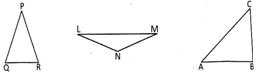
\[\Delta \] ABC is an equilateral triangle as AB = BC = AC = 4 cm.
Note: All the angles of an equilateral triangles are of \[{{60}^{o}}\]
![]() Isosceles Triangle
Isosceles Triangle
A triangle whose any two sides are of equal length is called isosceles triangle.
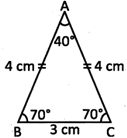
\[\Delta \] ABC is an isosceles triangle as AB = AC 5 cm.
Note: In an isosceles triangle, opposite angles of equal sides are equal
![]() Scalene Triangle
Scalene Triangle
A triangle whose all sides are of different length is called scalene triangle.
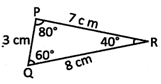
\[\Delta \] PQR is a scalene triangle as \[PQ\ne QR\ne PR.\]
Note: In a scalene triangle, no angles are equal
![]() Angle Based Classification
Angle Based Classification
On the basis of angles, triangle are of three types
(i) Acute-angled Triangle
(ii) Right-angled Triangle
(iii) Obtuse-angled Triangle
![]() Acute-Angled Triangle
Acute-Angled Triangle
A triangle having all angles between 90° and 0° is called acute-angled triangle.
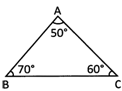
ABC is an acute-angled triangle as its each angle (\[\angle A,\angle B,\angle C\]) measures between \[{{0}^{o}}\] and \[{{90}^{o}}.\]
![]() Right-Angled Triangle
Right-Angled Triangle
A triangle having an angle of 90° is called a right-angled triangle.
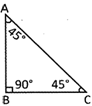
\[\Delta \]ABC is a right-angled triangle as it contains a right angle(\[\Delta ABC\])
![]() Obtuse-Angled Triangle
Obtuse-Angled Triangle
A triangle having one obtuse angle is called obtuse-angled triangle.
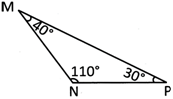
\[\Delta \]MNP is an obtuse-angled triangle as it contains an obtuse angle (\[\angle MNP\])
You need to login to perform this action.
You will be redirected in
3 sec
