Geometrical Basic Shapes
Category : 6th Class
![]() Point
Point
A dot which indicates position but not dimension is called a point. A point does not have length, breadth and height. P and Q are points in the figure below.
![]()
In the picture above, P and Q are points In the picture above two points lie on the same line and therefore called collinear points. Points do not lie on the same line are called non collinear points.
![]() Line
Line
A set of infinite points which can be extended infinite distance in both sides is called a line.
\[\] In the picture above, M is a line
Features of the Line
(i) The length of a line is infinite.
(ii) It has no terminal, therefore, can be extended infinitive in both directions.
(iii) It is made up of infinite points.
![]() Line Segment
Line Segment
A line of fix length is called line segment.
![]()
In the picture above, P and Q is a line segment and represented by \[\overline{PQ}.\]
![]() Features of the Line Segment
Features of the Line Segment
(i) A Line segment has fix length.
(ii) It has two end points.
![]() Ray
Ray
A ray is defined as the line that can be extended infinite in one direction.
![]()
In the picture above, end point of terminal point Ray AB is represented as AB
![]() Angle
Angle
Angle is formed between two rays which having common end point. Symbol of angle \[=\angle \]
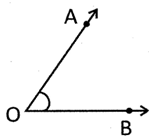
Vertex or common end point = 0 Arms of angle \[\angle AOB\] = OA and OB the name of the above angle can be \[\angle \text{ }AOB\]or \[\angle BOA\] The unit of measurement of an angle is degree \[{{(}^{o}})\]
![]() Types of Angles
Types of Angles
There are various types of angles which are the following:
Acute Angle
The angle between 0° and 90° is called an acute angle.
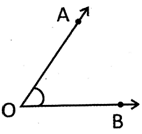
In the picture above \[\angle AOB\]or \[\angle BOA\] is an acute angle. The inclined arm OA on the horizontal is less inclined than vertical line. \[{{10}^{o}},{{30}^{o}},{{60}^{o}},{{80}^{o}}\] are acute angles.
Right Angle
An angle of \[{{90}^{o}}\] is called right angle.
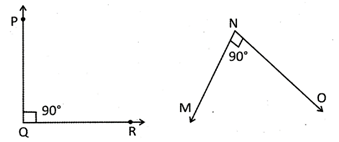
Obtuse Angle
An angle whose measure is between \[{{90}^{o}}\] and \[{{180}^{o}}\] is called an obtuse angle.
Straight Angle
An angle whose measure is \[{{180}^{o}}\]is called straight angle. Or an angle formed between two opposite rays is called straight angle.
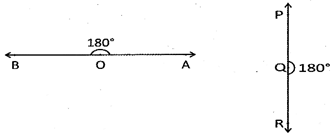
Reflex Angle
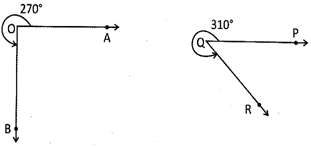
An angle whose measure is more than \[{{180}^{o}}\] and less then \[{{360}^{o}}\] is called reflex angle.
Complementary angle
Two angles whose sum is \[{{90}^{o}}\] is called the complimentary of each other \[{{60}^{o}}+{{30}^{o}}={{90}^{o}}\]
Complementary angle of \[{{60}^{o}}={{90}^{o}}-{{60}^{o}}={{30}^{o}}\]
Complementary angle of \[{{30}^{o}}={{90}^{o}}-{{30}^{o}}={{60}^{o}}\]
Complementary angle of \[\text{ }\!\!\theta\!\!\text{ }=90-\text{ }\!\!\theta\!\!\text{ }\]
The complementary angle of a given angle
\[={{90}^{o}}-\] the given angle.
Therefore, if thesum of two angles is 90° then they are called complementary angles to each other.
Supplementary Angle
Two angles whose sum is \[{{180}^{o}}\] is called supplementary angles. \[{{120}^{o}}+{{60}^{o}}={{180}^{o}}\]
Supplementary Angle of \[{{120}^{o}}={{180}^{o}}-{{120}^{o}}={{60}^{o}}\]
Supplementary Angle of \[{{60}^{o}}={{180}^{o}}-{{60}^{o}}={{120}^{o}}\]
The supplementary angle of the given angle \[=\text{ }{{180}^{o}}-\] the given angle Supplementary angle of \[\text{ }\!\!\theta\!\!\text{ }={{180}^{o}}-\text{ }\!\!\theta\!\!\text{ }\]
Equal Angles
If the measurement of two angles is equal then they are called equal angles.
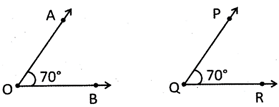
In the picture above, the measurement of the angles is equal. Therefore, \[\angle AOB\]and \[\angle PQR\]are equal angles.
Adjacent Angle
Two angles are said to be adjacent even if they have common vertex and one common arm. In \[\angle AOC\]
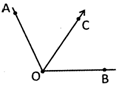
Vertex = O
Arms = OA, OC
Arms = OC, OB
Hence vertex 0 and arm OC is common so these two angles AOC and COB are adjacent angles.
Vertically Opposite Angle
Two angles are said to be vertically opposite angles if they are formed by opposite rays having common vertex.
Vertically opposite angles are formed by two lines which intersects each other.
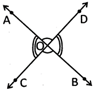
In the picture above, \[\angle AOD\]and \[\angle BOC\]are vertically opposite angles. They are formed by opposite rays and they have same or common end point 0.
Similarly, \[\angle AOC\]and \[\angle BOD\]are vertically opposite angles.

![]() The measurement of an angle is 180°. Which one of the following types of angle is this?
The measurement of an angle is 180°. Which one of the following types of angle is this?
(a) Right angle
(b) Straight angle
(c) Reflex angle
(d) All of these
(e) None of these
Answer: (b)
Explanation
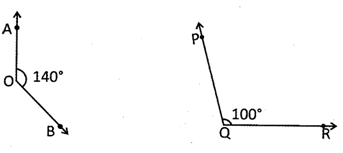
![]() A straight angle has a measurement of 180° . Which one of the following is the complementary angle of 30°?
A straight angle has a measurement of 180° . Which one of the following is the complementary angle of 30°?
(a) \[{{30}^{o}}\]
(b) \[{{60}^{o}}\]
(c) \[{{90}^{o}}\]
(d) All of these
(e) None of these
Answer: (b)
Explanation
Complementary angle of \[{{30}^{o}}={{90}^{o}}-{{30}^{o}}={{60}^{o}}\]
![]() In the options given below the pair of angles are given. Find the complementary pair.
In the options given below the pair of angles are given. Find the complementary pair.
(a) \[{{51}^{o}},{{25}^{o}}\]
(b) \[{{61}^{o}},{{29}^{o}}\]
(c) \[{{45}^{o}},{{55}^{o}}\]
(d) All of these
(e) None of these
Answer: (b)
Explanation
If the sum of pair of angles is \[{{90}^{o}}\] then the pair is called complementary pair of angles. The sum of angles \[~{{61}^{o}}+{{29}^{o}}={{90}^{o}}.\] Hence the pair of angles \[{{61}^{o}},{{29}^{o}}\] is a complementary pair of angles.
![]() Choose the pair of supplementary angle from the options given below?
Choose the pair of supplementary angle from the options given below?
(a) \[{{100}^{o}},{{200}^{o}}\]
(b) \[{{105}^{o}},{{75}^{o}}\]
(c) \[{{30}^{o}},{{180}^{o}}\]
(d) All of these
(e) None of these
Answer: (b)
Explanation
The sum of angles of the pair \[{{105}^{o}},{{75}^{o}}={{105}^{o}}+{{75}^{o}}={{180}^{o}}.\]Hence, the pair of angles \[{{105}^{o}},{{75}^{o}}\] is a supplementary pair of angles.
![]() Two figures are given below. Which one of the following options is correct for the adjacent angles if the line segment OB divides the AOC into two equal parts?
Two figures are given below. Which one of the following options is correct for the adjacent angles if the line segment OB divides the AOC into two equal parts?
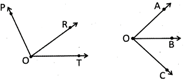
(a) AOB adjacent \[\angle BOC\]and \[\angle TOR\]adjacent \[\angle ROP\]
(b) \[\angle TOR\]adjacent\[\angle AOB\]and \[\angle ROP\]adjacent \[\angle AOB\]
(c) \[\angle POT\]adjacent\[\angle AOC\]
(d) All of these
(e) None of these
Answer: (a)
Explanation
Two angles said to be adjacent even if they have one common arm and one common vertex.
Hence,
\[\angle AOB\]adjacent \[\angle BOC\]and \[\angle TOR\]adjacent \[\angle ROP.\]
You need to login to perform this action.
You will be redirected in
3 sec
