7th Class Mathematics Lines and Angles Angle

     Angle                

 

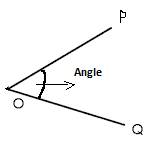
If two rays have common end point then the inclination between two rays is called angle. In the figure O is the vertex, \[\overline{OP}\] and \[\overline{OQ}\] are called arm of the angle. It is represented by notation\[\angle \].                

 

      Types of angle                

Acute Angle                

Tangle whose measure is more than \[0{}^\circ \] and less than \[90{}^\circ .\]                                

 

Right Angle                

The angle of measure \[90{}^\circ \]                                

 

Obtuse Angle                

The angle whose measure is more than 90° and less than \[180{}^\circ .\]                                

 

Straight Angle                

The angle whose measure is \[180{}^\circ \]                                

 

Reflex Angle                

The angle whose measure is more than \[180{}^\circ \]and less than \[360{}^\circ .\]                                

 

Complete Angle                

The angle whose measure is 360°.                                

 

Equal Angles                

Two angles are said to be equal if they are of same measure.                

 

      Complementary Angles                

If the sum of measure of two angles is \[{{90}^{o}}\] then they are said to be complementary angles .e.g \[75{}^\circ \] and \[15{}^\circ \] are complementary angles and they are said to be complement of each other.  

 

      Supplementary Angles                

If the sum of measure of two angles is \[180{}^\circ \]then they are said to be supplementary angles, e.g \[107{}^\circ \] and \[73{}^\circ \] are said to be supplement of each other.                

 

 

 

 

  Which one of the following statements is not true?                

(i) A line segment has finite length                

(ii) A line has only one dimension                

(iii) A line \[\overleftrightarrow{AB}\] and \[\overleftrightarrow{BA}\]represents the same                

(iv) A ray \[\overleftrightarrow{AB}\]and \[\overleftrightarrow{BA}\]represents the same                

(a) i, ii                                                   

(b) ii and iii                

(c) Only iv                                           

(d) iii and iv                

(e) None of these                                

 

Answer: (c)                

Explanation                

\[\]and \[\]are different rays. They are started from different end points A and B respectively.                

Therefore, option (c) is correct and rest of the options is incorrect.                

 

 

In the following AD is the bisector of \[\angle EAF\]                

               

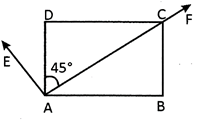
Which one of the following statements is incorrect?                

(a) \[\angle EAD\]is an acute angle                

(b) \[\angle BAE\]is an obtuse angle                

(c)\[\angle FAD\] and \[\angle DAE\]are complement to each other                

(d) \[\angle CAD\]and \[\angle DAE\]are not complement to each other                

(e) None of these                                

 

Answer: (d)                

Explanation                

Since \[\angle EAD=\angle CAD=45\]degree hence, option (a) is correct.                

\[\angle BAE\]is more than 90° therefore, it is obtuse hence, option (b) is also correct.                

The sum of \[\angle FAD\]and \[\angle DAE\]is \[90{}^\circ \] hence, option (c) is also correct                

\[\left( \angle CADand\text{ }\angle DAE \right)\]and \[\left( \angle FAD\text{ }and\text{ }\angle DAE \right)\]are the same. Therefore, they are also complement.                

 

 

If the difference of two supplementary angles is \[50{}^\circ \] then find the measurement of the smaller angle.                

(a) 67°                                                  

(b) \[75{}^\circ \]                

(c)\[~65{}^\circ \]                                           

(d) \[90{}^\circ \]                

(e) None of these                                

 

Answer: (c)                                

Explanation                

Let the one angle be x then other angle will be \[180{}^\circ -x.\]                

By given condition\[~x-(180{}^\circ -x)=50{}^\circ \]                

\[2x=180{}^\circ +50{}^\circ \Rightarrow 2x=230{}^\circ \text{ }\Rightarrow x=115{}^\circ \]                

Hence, the measurement of smaller angle \[=\text{ }180{}^\circ -115{}^\circ =65{}^\circ \]                

 

 

  Find the supplement of an angle which is 8 times of its complement.                

(a) 90°                                                  

(b) 100°                

(c) 80°                                                  

(d) 70°                

(e) None of these                                

 

Answer: (b)                  

 

 

If the angle and its complement are x and \[\sqrt{x}\] respectively then find the angle.                

(a)\[11{}^\circ ,\text{ }12{}^\circ \]                                         

(b) \[13{}^\circ ,\text{ }14{}^\circ \]                

(c)\[-15{}^\circ ,1{}^\circ \]                                         

(d) \[81{}^\circ \]                

(e) None of these                 

 

Answer: (d)  

 

      Adjacent Angles                

Two angles are said to be adjacent angles, if

• They have a common vertex
• They have common arm and
• Non-common arms are opposite to the common arm.  

In the given figure \[\angle POQ,\text{ }\angle QOR\] are adjacent angles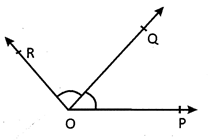                
               

 

        Linear Pair of Angles                

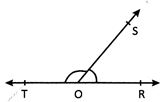
If the sum of measure of two adjacent angles is \[180{}^\circ \] then they are said to be linear pair of angles. In the linear pair non-common arms are opposite to each other.                                

In the figure \[\angle ROS\]and \[\angle TOS\]are linear pairs.                

 

 

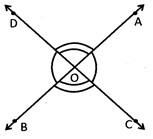
        Vertically Opposite Angles                

It is the pair of angle which is formed by two intersecting lines having no common arms. In the given figure \[\angle AOC\]and \[\angle BOD\]are vertically opposite angles. Similarly \[\angle AOD\]and \[\angle BOC\]are also vertically opposite angles.