8th Class Mathematics Squares and Square Roots Properties of Square Number

         Properties of Square Number  

            A Perfect Square Number can only end with Digits 0, 1, 4, 5, 6 and 9,

• If the last digit of a number is 0, its square ends with 00 and the preceding digits must also form a square.
• If the last digit of a number is 1 or 9, its square ends with 1 and the number formed by its preceding digits must be divisible by four.
• If the last digit of a number is 2 or 8, its square ends with 4 and the preceding digits must be even.
• If the last digit of a number is 3 or 7, its square ends with 9 and the number formed by its preceding digits must be divisible by four.
• If the last digit of a number is 4 or 6, its square ends with 6 and the preceding digits must be odd.
• If the last digit of a number is 5, its square ends with 5 and the preceding digits must be 2.
• A square number cannot be a perfect number.  

            Methods to Find Square of a Number

• If the number is in the form of m5, where m represents the preceding digits, its square is n25, where  and represents digits before 25. For example the square of 65 can be calculated by 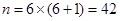Thus square of 65 is equal to 4225.
• If the number is in the form of m0 where m represents the preceding digits, its square is n00 where 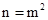. For example the square of 70 is 4900, where n = 49 & m = 7.
• If the number has two digits and it is in the form of 5m where m represents the unit digit, its square is AABB where AA = 25 + m and 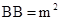Example: Calculate the square of 57. AA = 25 + 7 = 32 and BB = 49, it means .
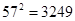• Squares of even numbers are even, since
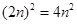
• Squares of odd numbers are odd, since 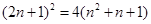. It follows that square roots of even square numbers are even and square roots of odd square numbers are odd.