9th Class Mathematics Statistics Pie Chart

         Pie Chart

A pie chart is the pictorial representation of the given data with the help of non intersecting sectors of different areas and different central angles. The magnitude of the central angles depend on the magnitude of the data. In a pie chart, the arc length of each sector (and consequently its central angles and area), is proportional to the quantity it represents. When angles are measured with 1 turn as unit then a number of percent is identified together with the same number of turns. The sectors create a full disk. It is named for its resemblance to a pie which has been sliced. The earliest known pie chart is generally credited to William Play fair's Statistical Breviary in 1801.

Pie chart of populations of English native speakers      

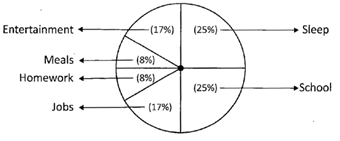
  The data in the table represents the percentage of hours of the day spent by the individuals on various activities of the day. Give the pictorial representation of the data given below:  

The Pictorial Representation of the Data given above in the Table  

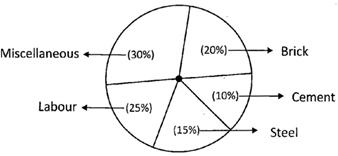
Calculation of Central Angles  

Steps of Constriction

• Draw a circle of any convenient radius.
• Draw a horizontal radius of the circle.
• Starting with the horizontal radius ,form sectors with central angle of 54,72,36,90 and 108 respectively.
• Shade the sectors differently and label them.
• Thus, we obtain the required pie chart, shown in the adjoining figure.  

• The following number is the only one of its kind. Can you figure out what is so special about it? 8,549,176,320. (It's the only number that contains all of the digits in English alphabetical order.)
• What is the great sign of Success for a teacher ...? He is able to say the students are doing their own.
• Among all shapes the circle has the shortest perimeter.
• Among all shapes the circle has the largest area.
• There are just five regular polyhedral.  

• There are various graphical representation of the data such as bar graph, histogram, pie chart, etc.
• A bar graph is used to show the comparison among the different quantities.
• A histogram is used to show the graph of the data that are in intervals.
• A pie chart is used to show the data which is the part of whole data.
• A polygon curve shows the data which changes continuously with the time.
• The graph is represented on the coordinate axis taken along the X-axis and Y-axis.
• The graph shows the relation between the dependent and independent variables.   

Answer the following question based on the graph given on previous page:  

  In the bar graph given in example, student?s favorite activity after school is:

(a) Talk on Phone                            

(b) Visiting Friends

(c) Earning Money                          

(d) Play Sports

(e) None of these  

Answer: (b)  

  According to the bar graph which is the least favorite activity after school?

(a) Talk on Phone                            

(b) Visiting Friends

(c) Earning Money                          

(d) Play Sports

(e) None of these  

Answer: (e)  

  Which two activities are favored equally by the students?

(a) Playing sports and earning money

(b) Using the computer and earning money

(c) Talking on the phone and playing sports

(d) All of these                 

(e) None of these  

Answer: (a)  

  There are several histograms as shown below, find which one of the following represents the histograms of the data given in the table below?  

(a)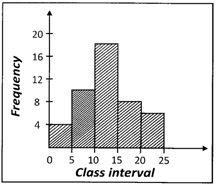                 

(b)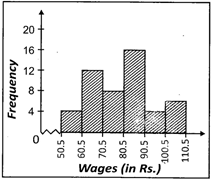

(c)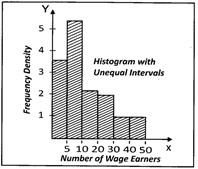                        

(d) All of these  

(e) None of these  

Answer: (a)

Explanation:

In the above examples, the intervals are exclusive.  

  The daily wages of 50 workers working for a factory is given below: In table (i) the class intervals are inclusive. So we convert them to the exclusive form as shown in table (ii).                          

(i)

(ii)

Which one of the following is the histogram of above given table?

(a)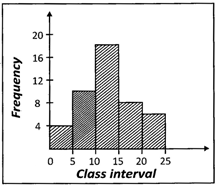

(b)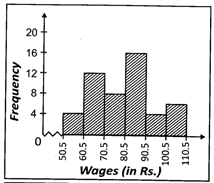

(c)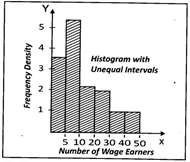                          

(d) All of these

(e) None of these  

Answer: (b)

Exploration:

(i) The class intervals are made continuous and then the histogram is constructed.

(ii) A kink or a zig - zag curve is shown near the origin. It indicates that the scale along the horizontal axis does not start at the origin.

(iii) The horizontal scale and vertical scale need not be the same.  

  Distribution of shops according to the number of wage - earners employed at a shopping complex is given below:  

Illustrate the above table by a histogram, showing clearly how you deal with the unequal class intervals

(a)                 

(b)

(c)                

(d) All of these

(e) None of these  

Answer: (c)

Explanation:

When the intervals are unequal, we construct each rectangle with the class intervals as base and frequency density as height

\[\text{Frequency density}=\frac{\text{Frequency of the class interval}}{\text{Class size of the interval}}\]