Venn Diagrams
Category : 8th Class
Introduction
A Venn diagram or set diagram is a diagram that shows all possible logical relations between a finite collection of different sets. They are used to illustrate simple set relationships in probability, logic, statistics etc.
The best method of solving the problems based on inference or deduction is Venn diagram.
Venn diagram is a way representing sets pictorially.
Various cases of Venn diagram
Case I:
An object is called a subset of another object, if the former is a part of the latter and such relation is shown by two concentric circles.
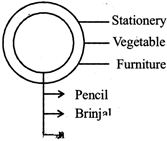
(i) Pencil, Stationery
(ii) Brinjal, Vegetable
(iii) Chair, Furniture
It is very clear from the above relationship that one object is a part of the other, and hence all such relationships can be represented by the figure shown.
Case II:
An object is said to have an intersection with in a other object that share some things in common.
(i) Surgeon, Males
(ii) Politicians, Indian
(iii) Educated, Unemployed
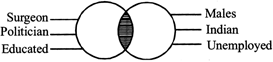
All the three relationships given above have something in common as some surgeons can be male and some female, some politicians may be Indian and some may belong to other countries, educated may be employed and unemployed as well and all the three relationships can be represented by the figure shown.
Case III:
Two objects are said to be disjoint when neither one is subset of another and nor do they share anything in common. In other words, totally unrelated objects fall under this type of relationship.
(i) Furniture, Car (ii) Copy, Cloth (iii) Tool, Shirt

It is clear from the above relationships that both the objects are unrelated to each other, and hence can be represented diagrammatically as shown in figure above. From the above discussion we observe that representation of the relationship between two objects is not typical if students follow the above points. But representation of three objects diagrammatically pose slight problems before the students.
ANALYTICAL METHOD:
Try to understand these type of questions using analytical method.
A statement always has a subject and a predicate:
All politicians are liars.
(subject) (predicate)
Basically, there are four types of sentences.
A - type \[\Rightarrow \] All politicians are liars.
I-type \[\Rightarrow \] Some politicians are liars
0-type \[\Rightarrow \] Some politicians are not liars
E-type \[\Rightarrow \] No politicians are liars
Conclusions can be drawn by taking two of the above statements together. The rules of conclusion are:
\[A+A=A\] \[A+E=E~\] \[I+A=I\]
\[I+E=0~~~~~~~\] \[E+A=0*~\] \[E+I=O*\]
Conclusion can only be drawn from the two statements if the predicate of the first statement is the subject of the second statement. The common term disappears in the conclusion and it consists of subject of the first statement and predicate of the second statement. For examples
\[A+A=A\]
(i) All boys are girls,
(ii) All girls are healthy
Conclusion: All boys are healthy.
\[A+E=E\]
(i) All boys are girls,
(ii) No girls are healthy
Conclusion: No boys are healthy.
\[I+A=I\]
(i) Some boys are girls,
(ii) All girls are healthy
Conclusion: Some boys are healthy.
\[I+E=0~~~~~~~\]
(i) Some boys are girls,
(ii) No girls are healthy
Conclusion: Some boys are not healthy.
\[E+I=O*\]
(i) No boys are girls,
(ii) All girls are healthy
Conclusion: Some healthy are not boys.
\[I+I=O*\]
(i) No boys are girls,
(ii) Some girls are healthy
Conclusion: Some healthy are not boys.
Miscellaneous Solved Examples
DIRECTIONS (Example 1 to 4): Each of these questions given below contains three group of things. You have to choose from the following four numbered diagrams, a diagram that depicts the correct relationship among the three groups of the things in each question.
(a)  (b)
(b) 
(c)  (d)
(d) 
EXAMPLE 1:
Moon, Earth, Universe
Sol, Moon and Earth are parts of the universe and therefore are subsets of universe and hence this relationship is represented by diagram (a)
EXAMPLE 2:
India, Pakistan, Asia
Sol. India and Pakistan, are the subsets of Asia. Hence, option
(a) represents this relationship.
EXAMPLE 3:
Batsman, Cricket, Stick
Sol. Batsman, is a subset of Cricket and, Stick is something unrelated to Cricket, therefore, our answer is (d).
EXAMPLE 4:
Book, Pen, Pencil
Sol. Book, Pen, Pencil are neither subset of one another nor have anything in common. Therefore, our answer is (c)
EXAMPLE 5:
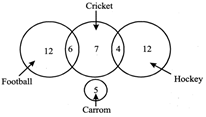
In a class of 46 students, 18 played football, 17 played cricket including 6 who played football. 16 students played hockey including 4 who played cricket, but not football. Five students played carrom but no outdoor games. Which of the following figure represents these facts?
(a) 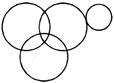 (b)
(b) 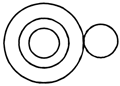
(c) 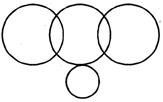 (d)
(d) 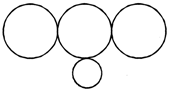
EXAMPLE 6:
A result of a survey of 100 persons with respect with respect to their knowledge of Hindi (H), English (E) and Sanskrit (S) is given below.
What is the ratio of these who know all the three languages to those who do not know Sanskrit?
(a) \[\frac{1}{9}\] (b) \[\frac{1}{10}\]
(c) \[\frac{10}{17}\] (d) \[\frac{5}{27}\]
Sol. (d)
The persons who know all the three language are represented by the region which is common to all the three circles.
So, number of such persons = 100.
The persons who do not know Sanskrit are represented by the region outside circle S.
So, number of such persons
\[=(200+120+220)=540.\]
\[\therefore \] Required ratio \[100:540=5:27\]
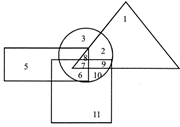
Directions (Example 7 to 11): In the following figure, rectangle, square, circle and triangle represent the regions of wheat, gram, maize and rice cultivation respectively. On the basis of the above figure, answer the following questions.
EXAMPLE 7:
Which area is cultivated by all the four commodities?
(a) 7 (b) 8
(c) 9 (d) 2
Sol, (a)
The required region is the one common to the rectangle, square, circle and the triangle i.e., 7.
EXAMPLE 8:
Which area is cultivated by wheat and maize only?
(a) 8 (b) 6
(c) 5 (d) 4
Sol. (d)
The required region is the one which is common to only the rectangle and the circle and is not a part of either the triangle or the square i.e., 4.
EXAMPLE 9:
Which area is cultivated by rice only?
(a) 5 (b) 1
(c) 2 (d) 11
Sol. (b)
The required region is the one which lies inside the triangle and outside the rectangle. Square and circle i.e.,1.
EXAMPLE 10:
Which area is cultivated by maize only?
(a) 10 (b) 2
(c) 3 (d) 4
Sol. (c)
The required region is the one which lies inside the circle but outside the rectangle square and triangle i.e., 3.
EXAMPLE 11:
Which area is cultivated by rice and maize and nothing else?
(a) 9 (b) 8
(c) 2 (d) 7
Sol. (c)
The required region is the one which is common to only the triangle and the circle i.e., 2.
Directions (Example 12 to 14): From the following diagram choose the option that best illustrates the relationship between the three classes given in each of the question that follows.


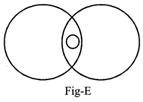
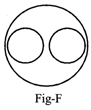
EXAMPLE 12:
Pepsi, Coca-Cola, Drink
Sol. (F)
Pepsi and Coca-Cola are different but both are Drinks.
EXAMPLE 13:
Men, Women, Children
Sol. (E)
Men and Women have separate identity. Children are common.
EXAMPLE 14:
Criminals, Thief, Smuggler
Sol. (F)
Both ‘Thief’ and Smuggler are criminals.
Directions for Example 15: In fig there are three interlocking circle, I, S and P where circle I stands for Indian, circle S for scientists, and circle P for politicians. Different regions of the figure are lettered from a through g.
(i) Indians who are politicians but not scientists.
(ii) Scientists who are Indians but not politicians.
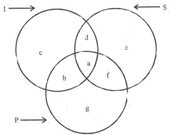
(iii) Non-Indian scientists who are politicians.
(iv) Non-scientist Indians who are not politicians.
(v) Politician – scientists who are Indians.
(a) Indians who are politicians but not scientists.
Let us use the symbol \[\cap \] for intersection of two sets.
Then | \[\cap \]P represents the set of people who are Indians and politicians, i.e., region ‘a’ and ‘b’ Now ‘a’ is part of S also. Hence ‘a’ represents Indians who mare scientists and politicians.
‘b’ is not part of ‘S’ Hence ‘b’ represents Indians who are politicians but not scientists. Hence ‘b’ is the required answer.
(b) Scientists who are Indians
This set is represented by the region which is in the intersection of S and I but not in P. Hence ‘d’ is the required answer.
(c) Non-Indian scientists who are politicians. The region which is in S \[\cap \]P but not in I is ‘f’
(d) Non-scientist Indians who are not politicians.
The region in I but not in S nor in P is the desired region Hence ‘c’ is the required answer.
(5) Politicians – scientists who are Indians. This is the region common to all the three sets.
hence ‘a’ is the required answer.
EXAMPLE 15:
In fig which one of the following statements is not true?
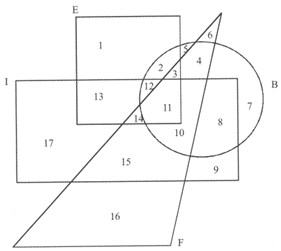
(a) All farmers who are employed are either backward or illiterate or both.
(b) Some unemployed farmers are backward and illiterate.
(c) Some backward farmers who are employed are not illiterate.
(d) All backward persons who are not illiterate are either farmers or employed or both.
Sol. (a) All farmers who are employed are in the regions 3,11 and 14. Region 3 lies in B, 14 lies in I and II lies in both B and I. Hence, the statement (a) is true. We are however looking for a statement which is not true.
(b) Some unemployed farmers should lie in B and I both. Unemployed farmers includes regions no. 4,6,10,15 and 16, Since one of the region i.e,' 10' lies both in I and B the statement is true.
(c) Similarly, we can find out that statement (c) is true. Analyse (d) and (5) and find which one is not true.
EXAMPLE 16:
Below are given sets of objects. The objects in a set are related with one another in some manner.
Sol. There are an equal number of Venn diagrams representing each set on the basis of the relationship between the objects but the Venn diagrams are not arranged in the same order. You have to match each diagram with the appropriate set.
(i) Living beings, men, women
(ii) Primary, secondary schools B
(iii) Buffalo, pig, camel
(iv) Ribbon black, belt
(v) Rectilinear figures, quadrilaterals, circles
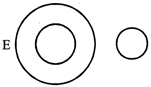
(vi) Polygons, trapezium, quadrilaterals
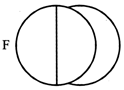
(vii) Men, doctors, specialisation.
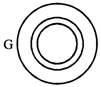
(viii) Year, February, leap year
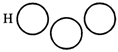
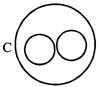
Sol. (i) Men and women are both different but they form subsets of living beings. Diagram C represents this situation.
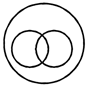
(ii) Primary and secondary are both schools and some secondary schools have primary departments. Diagram B represents this relation.
(iii) Buffalo, pig, camel are three different objects. Diagram H represents this relation.
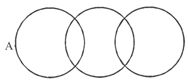
(iv) Some ribbons and some belts are black. Ribbons and belts are different. Diagram A represents this relation.
(v) All quadrilaterals are rectilinear figures but circles are different. Diagram E shows this relation.
(vi) Polygons contain all quadrilaterals and quadrilaterals contains all trapeziums. Diagram G depicts this relation
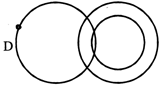
(vii) some men are doctors and some doctors have specialisation. Diagram D describes this relation,
(viii) Leap year is longer than a regular year and February contains this extra period. Diagram F indicate this relation.
Directions for Example 17: Each statements has three segments. Choose the alternative where the third segment can be logically deduced using both the preceding two, but not just from one of them.
(A) Some roses are flowers, some flowers do not stink. Some stinking thing are not rose.
(B) Some sheep are black. Some black things are invisible. Some sheep are invisible.
(C) Some parrots are green. All greens are grass. Some grass are not parrot.
(D) Some library contains books. Some books contain pages. Some library contains pages.
(a) A and D (b) B and D
(c) C and D (d) None follows
Sol. (d)
(a) 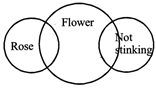
(b) 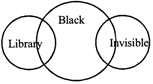
(c) 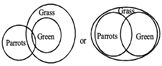
(d) 
You need to login to perform this action.
You will be redirected in
3 sec
