Cyclic Quadrilateral
Category : JEE Main & Advanced
A quadrilateral PQRS is said to be cyclic quadrilateral if there exists a circle passing through all its four vertices P, Q, R and S.
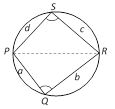
Let a cyclic quadrilateral be such that
\[PQ=a,\,QR=b,\,RS=c\] and \[SP=d\].
Then\[\angle Q+\angle S={{180}^{o}}\],\[\angle A+\angle C={{180}^{o}}\]
Let \[2s=a+b+c+d\]
Area of cyclic quadrilateral = \[\frac{1}{2}(ab+cd)\sin Q\]
Also, area of cyclic quadrilateral = \[\sqrt{(s-a)(s-b)(s-c)(s-d)}\], where \[2s=a+b+c+d\] and \[\cos Q=\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}-{{d}^{2}}}{2(ab+cd)}\].
(1) Circumradius of cyclic quadrilateral : Circum circle of quadrilateral PQRS is also the circumcircle of \[\Delta PQR\]. \[R=\frac{1}{4\Delta }\sqrt{(ac+bd)(ad+bc)(ab+cd)}=\frac{1}{4}\sqrt{\frac{(ac+bd)(ad+bc)(ab+cd)}{(s-a)(s-b)(s-c)(s-d)}}\].
(2) Ptolemy's theorem : In a cyclic quadrilateral PQRS, the product of diagonals is equal to the sum of the products of the length of the opposite sides i.e., According to Ptolemy's theorem, for a cyclic quadrilateral PQRS \[PR.QS=PQ.RS+RQ.PS.\]

You need to login to perform this action.
You will be redirected in
3 sec
