JEE Main & Advanced Mathematics Trigonometric Equations Regular Polygon

A regular polygon is a polygon which has all its sides equal and all its angles equal.

(1) Each interior angle of a regular polygon of n sides is \[\left( \frac{2n-4}{n} \right)\times \]right angles \[=\left[ \frac{2n-4}{n} \right]\times \frac{\pi }{2}\] radians.

(2) The circle passing through all the vertices of a regular polygon is called its circumscribed circle.

If \[a\] is the length of each side of a regular polygon of \[n\] sides, then the radius \[R\] of the circumscribed circle, is given by  \[R=\frac{a}{2}\,.\,\text{cosec }\left( \frac{\pi }{n} \right)\]             

(3) The circle which can be inscribed within the regular polygon so as to touch all its sides is called its inscribed circle.

Again if \[a\] is the length of each side of a regular polygon of \[n\] sides, then the radius \[r\] of the inscribed circle is given by \[r=\frac{a}{2}\,.\,\text{cot }\left( \frac{\pi }{n} \right)\]

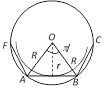
(4) The area of a regular polygon is given by \[\Delta =n\,\,\times \] area of triangle \[OAB\]

\[=\frac{1}{4}n{{a}^{2}}\cot \,\left( \frac{\pi }{n} \right),\]    (in terms of side)

\[=n{{r}^{2}}\,.\,\tan \,\left( \frac{\pi }{n} \right),\]      (in terms of in-radius)

\[=\frac{n}{2}\,.\,{{R}^{2}}\sin \,\left( \frac{2\pi }{n} \right),\] (in terms of circum-radius)