JEE Main & Advanced Mathematics Trigonometric Equations Relation Between Sides and Angles

A triangle has six components, three sides and three angles. The three angles of a \[\Delta ABC\] are denoted by letters \[A,\,\,B,\,\,C\] and the sides opposite to these angles by letters \[a,\,\,b\] and \[c\] respectively. Following are some well known relations for a triangle (say \[\Delta ABC\])  

• \[A+B+C={{180}^{o}}\] (or \[\pi \])
• \[a+b>c,\,\,b+c>a,\,\,c+a>b\]
• \[|a-b|<c,|b-c|<a,|c-a|<b\]

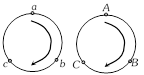
Generally, the relations involving the sides and angles of a triangle are cyclic in nature, e.g. to obtain the second similar relation to \[a+b>c,\] we simply replace \[a\] by \[b,\,\,b\] by \[c\] and \[c\] by \[a\]. So, to write all the relations, follow the cycles given.

The law of sines or sine rule : The sides of a triangle are proportional to the sines of the angles opposite to them  i.e., \[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=k,\,(say)\]

More generally, if \[R\] be the radius of the circumcircle of the triangle \[ABC,\,\,\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\].