JEE Main & Advanced Mathematics Vector Algebra Properties of Vectors

(1) Addition of vectors

 

 

(i) Triangle law of addition : If  in a \[\Delta ABC\], \[\overrightarrow{AB}=\mathbf{a}\] \[\overrightarrow{BC}=\mathbf{b}\]  and \[\overrightarrow{AC}=\mathbf{c}\], then \[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\] i.e., \[\mathbf{a+b+c}\].

 

 

 

 

 

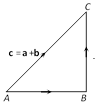
(ii) Parallelogram law of addition : If in a parallelogram \[OACB,\] \[\overrightarrow{OA}=\mathbf{a},\,\overrightarrow{OB}=\mathbf{b}\] and \[\overrightarrow{OC}\,=\mathbf{c}\]

 

 

 

 

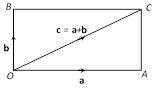
Then \[\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}\] i.e., \[\mathbf{a}+\mathbf{b}=\mathbf{c}\ \], where OC is a diagonal of the parallelogram OABC.

 

 

(iii) Addition in component form : If the vectors are defined in terms of \[\mathbf{i,}\,\,\,\mathbf{j}\] and \[\mathbf{k,}\] i.e.,  if \[\mathbf{a}={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\], then their sum is defined as \[\mathbf{a}+\mathbf{b}=({{a}_{1}}+{{b}_{1}})\mathbf{i}+({{a}_{2}}+{{b}_{2}})\mathbf{j}+({{a}_{3}}+{{b}_{3}})\mathbf{k}\]. 

 

 

Properties of vector addition : Vector addition has the following properties.

 

 

(a) Binary operation : The sum of two vectors is always a vector.

 

 

(b) Commutativity : For any two vectors \[\mathbf{a}\] and \[\mathbf{b}\],  \[\mathbf{a}+\mathbf{b}=\mathbf{b}+\mathbf{a}\].

 

 

(c) Associativity : For any three vectors \[\mathbf{a},\,\mathbf{b}\] and \[\mathbf{c}\], \[\mathbf{a}+(\mathbf{b}+\mathbf{c})=(\mathbf{a}+\mathbf{b})+\mathbf{c}\].

 

 

(d) Identity : Zero vector is the identity for addition. For any vector \[\mathbf{a},\,\,\mathbf{0}+\mathbf{a}=\mathbf{a}=\mathbf{a}+\mathbf{0}\]

 

 

(e) Additive inverse : For every vector \[\mathbf{a}\] its negative vector \[-\mathbf{a}\] exists such that \[\mathbf{a}+(-\mathbf{a})=(-\mathbf{a})+\mathbf{a}=\mathbf{0}\] i.e., \[(-\mathbf{a})\] is the additive inverse of the vector \[\mathbf{a}\]. 

 

 

(2) Subtraction of vectors : If  \[\mathbf{a}\]and \[\mathbf{b}\] are two vectors, then their subtraction \[\mathbf{a}-\mathbf{b}\] is defined as\[\mathbf{a}-\mathbf{b}=\mathbf{a}+(-\mathbf{b})\]  where \[-\mathbf{b}\] is the negative of \[\mathbf{b}\] having magnitude equal to that of \[\mathbf{b}\] and direction opposite to \[\mathbf{b}\]. If \[\mathbf{a}={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\],  \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\]

 

 

Then \[\mathbf{a}-\mathbf{b}=({{a}_{1}}-{{b}_{1}})\mathbf{i}+({{a}_{2}}-{{b}_{2}})\mathbf{j}+({{a}_{3}}-{{b}_{3}})\mathbf{k}\].

 

 

 

 

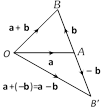
Properties of vector subtraction  

 

 

(i) \[\mathbf{a}-\mathbf{b}\ne \mathbf{b}-\mathbf{a}\]

 

 

(ii) \[(\mathbf{a}-\mathbf{b})-\mathbf{c}\ne \mathbf{a}-(\mathbf{b}-\mathbf{c})\]

 

(iii) Since any one side of a triangle is less than the sum and greater than the difference of the other two sides, so for any two vectors \[a\] and \[b,\] we have

 

 

(a) \[|\mathbf{a}+\mathbf{b}|\,\le \,|\mathbf{a}|+|\mathbf{b}|\]                               

 

 

(b) \[|\mathbf{a}+\mathbf{b}|\,\ge \,|\mathbf{a}|-|\mathbf{b}|\]

 

 

(c) \[|\mathbf{a}-\mathbf{b}|\,\le \,|\mathbf{a}|+|\mathbf{b}|\]                

 

(d) \[|\mathbf{a}-\mathbf{b}|\,\ge \,|\mathbf{a}|\,-\,|\mathbf{b}|\]

 

 

(3) Multiplication of a vector by a scalar : If \[\mathbf{a}\] is a vector and \[m\] is a scalar (i.e., a real number) then \[m\mathbf{a}\] is a vector whose magnitude is \[m\] times that of \[\mathbf{a}\] and whose direction is the same as that of \[\mathbf{a}\], if m is positive and opposite to that of \[\mathbf{a}\], if m is negative.

 

 

Properties of Multiplication of vectors by a scalar : The following are properties of multiplication of vectors by scalars, for  vectors \[\mathbf{a},\,\mathbf{b}\] and scalars \[m,\,\,n\].                                          

 

 

(i) \[m(-\mathbf{a})=(-m)\,\mathbf{a}=-(m\mathbf{a})\] 

 

 

(ii) \[(-m)\,(-\mathbf{a})=m\mathbf{a}\]           

 

 

(iii) \[m\,(n\mathbf{a})=(mn)\,\mathbf{a}=n(m\mathbf{a})\]          

 

 

(iv) \[(m+n)\,\mathbf{a}=m\mathbf{a}+n\mathbf{a}\]

 

 

(v) \[m\,(\mathbf{a}+\mathbf{b})=m\mathbf{a}+m\mathbf{b}\]

 

 

(4) Resultant of two forces

 

 

Let \[\overrightarrow{P}\] and \[\overrightarrow{Q}\] be two forces and \[\overrightarrow{R}\] be the resultant of these two forces then, \[\overrightarrow{R}\,=\overrightarrow{P}+\overrightarrow{Q}\]

 

 

 

 

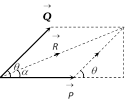
\[|\overrightarrow{R}|=R=\sqrt{{{P}^{2}}+{{Q}^{2}}+2PQ\,\cos \theta }\]

 

 

where \[|\overrightarrow{P}|=P,\,|\overrightarrow{Q}|=Q,\] 

 

 

Also, \[\tan \alpha =\frac{Q\sin \theta }{P+Q\cos \theta }\]

 

 

Deduction : When \[|\overrightarrow{P}|=|\overrightarrow{Q}|\],

 

 

i.e., \[P=Q,\,\,\tan \alpha =\frac{P\sin \theta }{P+P\cos \theta }=\frac{\sin \theta }{1+\cos \theta }=\tan \frac{\theta }{2}\];

 

 

 \[\therefore \]   \[\alpha =\frac{\theta }{2}\]

 

 

Hence, the angular bisector of two unit vectors \[\mathbf{a}\] and \[\mathbf{b}\] is along the vector sum \[\mathbf{a}+\mathbf{b}\].