-
question_answer1)
Find the general term of the series 4,7, 10,13......
A)
3n - 7 done
clear
B)
3n + 7 done
clear
C)
3n +1 done
clear
D)
3n ? 1 done
clear
View Solution play_arrow
-
question_answer2)
Which is the first negative term of the arithmetic progression 35, 30, 25,.....?
A)
7th term done
clear
B)
5th term done
clear
C)
9th term done
clear
D)
11th term done
clear
View Solution play_arrow
-
question_answer3)
Find the next term of the arithmetic progression \[\sqrt{12},\sqrt{27},\sqrt{48}\]
A)
\[\sqrt{75}\] done
clear
B)
\[\sqrt{60}\] done
clear
C)
\[\sqrt{80}\] done
clear
D)
\[\sqrt{90}\] done
clear
View Solution play_arrow
-
question_answer4)
What is the term of an arithmetic progression whose sum to 'n' terms is\[2{{n}^{2}}-3n\]?
A)
4n - 3 done
clear
B)
4n ? 5 done
clear
C)
4n + 5 done
clear
D)
5 - 4n done
clear
View Solution play_arrow
-
question_answer5)
Which term of the arithmetic progression 30, 27, 24,.... is O?
A)
8th term done
clear
B)
10th term done
clear
C)
13th term done
clear
D)
11th term done
clear
View Solution play_arrow
-
question_answer6)
The numbers 28, 22, 'x', 'y', 4 are in arithmetic progression. What are the respective values of 'x' and 'y'?
A)
10, 16 done
clear
B)
20, 18 done
clear
C)
18, 16 done
clear
D)
16, 10 done
clear
View Solution play_arrow
-
question_answer7)
What is the sum to 'n' terms of the series\[\sqrt{5},\sqrt{20},\sqrt{45},\sqrt{80},.....?\]
A)
\[\frac{n(n+1)\sqrt{5}}{2}\] done
clear
B)
\[\frac{n(n+1)}{\sqrt{2}}\] done
clear
C)
\[\frac{n}{2}\left( \frac{(n+1)}{\sqrt{5}} \right)\] done
clear
D)
\[n(n+1)\sqrt{5}\] done
clear
View Solution play_arrow
-
question_answer8)
What is the sum of the first 'n' even numbers?
A)
\[{{n}^{2}}+1\] done
clear
B)
\[n(n-1)\] done
clear
C)
\[{{n}^{2}}-n\] done
clear
D)
\[n(n+1)\] done
clear
View Solution play_arrow
-
question_answer9)
What is the sum of first 'n' odd numbers starting from 11?
A)
\[{{n}^{2}}+10n\] done
clear
B)
\[{{n}^{2}}-10n\] done
clear
C)
\[10n-{{n}^{2}}\] done
clear
D)
\[{{n}^{2}}\] done
clear
View Solution play_arrow
-
question_answer10)
How many two digit numbers are divisible by 4?
A)
20 done
clear
B)
16 done
clear
C)
25 done
clear
D)
22 done
clear
View Solution play_arrow
-
question_answer11)
How many terms of the arithmetic progression 1, 9, 17, .... must be taken to give a sum of 1540?
A)
10 done
clear
B)
40 done
clear
C)
20 done
clear
D)
15 done
clear
View Solution play_arrow
-
question_answer12)
What is the sum of 36 terms of the series whose\[{{n}^{th}}\]term is 5n + 4?
A)
4347 done
clear
B)
3474 done
clear
C)
4374 done
clear
D)
3447 done
clear
View Solution play_arrow
-
question_answer13)
Divide 21 into three parts that are in arithmetic progression and whose product is 168.
A)
3, 6, 9 done
clear
B)
14, 17, 11 done
clear
C)
2, 6, 14 done
clear
D)
2, 7, 12 done
clear
View Solution play_arrow
-
question_answer14)
Which term of the arithmetic progression 3, 8, 13, ..... is 55 more than its 20th term?
A)
29th term done
clear
B)
31st term done
clear
C)
25th term done
clear
D)
27th term done
clear
View Solution play_arrow
-
question_answer15)
Identify the formula for then\[{{n}^{th}}\]term of the arithmetic progression whose first term, [a] is 2 - x, and the common difference, [d] is 'x'.
A)
\[2+x-nx\] done
clear
B)
\[2+(n-2)x\] done
clear
C)
\[2-x-nx\] done
clear
D)
\[2+(n-1)x\] done
clear
View Solution play_arrow
-
question_answer16)
Find the number of terms of the arithmetic progression\[\frac{1}{3},\frac{1}{2},\frac{2}{3},......\frac{11}{6}\]
A)
8 done
clear
B)
10 done
clear
C)
12 done
clear
D)
13 done
clear
View Solution play_arrow
-
question_answer17)
The first, second and last terms of an arithmetic progression are 5, 9 and 101 respectively. Find the number of terms in the arithmetic progression.
A)
30 done
clear
B)
50 done
clear
C)
25 done
clear
D)
75 done
clear
View Solution play_arrow
-
question_answer18)
Find the sum of the first 18 terms, of the arithmetic progression 12b, 8b, 4b,......
A)
126b done
clear
B)
-56b done
clear
C)
256b done
clear
D)
- 288b done
clear
View Solution play_arrow
-
question_answer19)
Find the sum of the arithmetic progression, \[x-2y,2x-y,3x......11x+8y\].
A)
\[33(2x+y)\] done
clear
B)
\[22(2x+y)\] done
clear
C)
\[28(x+y)\] done
clear
D)
\[33x+11y\] done
clear
View Solution play_arrow
-
question_answer20)
Find the sum from the sixth term to the twelfth term of the arithmetic progression 6, 10, 14, ....
A)
176 done
clear
B)
232 done
clear
C)
266 done
clear
D)
184 done
clear
View Solution play_arrow
-
question_answer21)
The first term and the common difference of an arithmetic progression are 13 and 5 respectively. Find the sum from the 6th term to the 20th term.
A)
876 done
clear
B)
146 done
clear
C)
1095 done
clear
D)
1080 done
clear
View Solution play_arrow
-
question_answer22)
Find the value of 'n' if the sum of the first 'n' terms of the A.P.I 5, 23, 31, ....... is 708.
A)
9 done
clear
B)
8 done
clear
C)
12 done
clear
D)
10 done
clear
View Solution play_arrow
-
question_answer23)
A piece of wire is used to make circles of the following pattern.
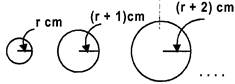
The radius of the first circle is 'r' cm and it is increased by 1 cm successively. Find the length of the wire that is required to make 5 such circles.
A)
\[(10\pi +r)cm\] done
clear
B)
\[2\pi \,cm\] done
clear
C)
\[10\pi (r+2)\,cm\] done
clear
D)
\[2\pi (r+2)\,cm\] done
clear
View Solution play_arrow
-
question_answer24)
An arithmetic progression has a 3rd term of 13 and a last term of 148. If the common difference is 5, find the number of terms of the progression.
A)
30 done
clear
B)
40 done
clear
C)
50 done
clear
D)
75 done
clear
View Solution play_arrow
-
question_answer25)
Given that the sum of the first 'n' terms of an arithmetic progression is 2n2 + 3n, find the twelfth term.
A)
\[{{7}^{2}}\] done
clear
B)
\[36\] done
clear
C)
\[\sqrt{625}\] done
clear
D)
56 done
clear
View Solution play_arrow
-
question_answer26)
The first two terms of an arithmetic progression are 27 and 24 respectively. How many terms of the progression are to be added to get - 30?
A)
15 done
clear
B)
20 done
clear
C)
25 done
clear
D)
18 done
clear
View Solution play_arrow
-
question_answer27)
A secondary school had an enrolment of 1620 students in the year 2009 which increases by 150 students per year. What was the enrolment in the year 2013?
A)
2170 done
clear
B)
2070 done
clear
C)
2220 done
clear
D)
2150 done
clear
View Solution play_arrow
-
question_answer28)
A piece of wire is used to make rectangles with the same height of 'h' cm. The lengths of the rectangles are increased by 1 cm successively.

Find the total length of wire required to make 7 rectangles in this pattern.
A)
\[\text{2 }\!\![\!\!\text{ h }+\text{ b }+\text{ 7 }\!\!]\!\!\text{ }\] done
clear
B)
2b + h + 7 done
clear
C)
2n + h + 6 done
clear
D)
\[\text{2 }\!\![\!\!\text{ b }+\text{ h }+\text{ 6 }\!\!]\!\!\text{ }\] done
clear
View Solution play_arrow
-
question_answer29)
The postal rates in India from town M to town N are tabulated as shown.
| Weight (g) | 1-60 | 61-80 | 81-100 | 101-120 | 121-140 |
| Postal Rate(Rs.) | 3.00 | 3.50 | 4.00 | 4.50 | 5.00 |
Amir posts a 230 g parcel from town M to town N, what is the postal charge?
A)
Rs. 8.00 done
clear
B)
Rs. 7.50 done
clear
C)
Rs. 7.00 done
clear
D)
Rs. 6.00 done
clear
View Solution play_arrow
-
question_answer30)
A cineplex has 13 rows of seats with 10 seats in the first row, 12 in the second, 14 in the third and so on. What is the total number of seats in the cineplex?
A)
252 done
clear
B)
256 done
clear
C)
258 done
clear
D)
286 done
clear
View Solution play_arrow
-
question_answer31)
Sulekha intends to read a 200 page book within a specific period-She starts by reading 11 pages on the first day and increases her rate of reading by reading an extra 2 pages for each subsequent day How long will she take to finish reading the book?
A)
20 done
clear
B)
10 done
clear
C)
15 done
clear
D)
25 done
clear
View Solution play_arrow
-
question_answer32)
The 6th term of an arithmetic progression is 30 and the sum of the first six terms is 210. Find the sum of the next 6 consecutive terms.
A)
100 done
clear
B)
50 done
clear
C)
138 done
clear
D)
204 done
clear
View Solution play_arrow
-
question_answer33)
The given figure shows a pattern of several squares drawn consecutively.
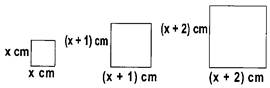
The perimeters of the squares in figure form an arithmetic progression. The length of the first square is x cm and the length of the other consecutive squares differ from each other by 1 cm. Given the sum of the perimeters of the first five squares is 160 cm, find the sum of the perimeters of the first 10 squares.
A)
280 cm done
clear
B)
240 cm done
clear
C)
420 cm done
clear
D)
360 cm done
clear
View Solution play_arrow
-
question_answer34)
In an arithmetic progression, the fourth term is 8 and the sum of 12 terms is 156. Find the value of 'p' if the \[{{p}^{th}}\]term is 1000.
A)
200 done
clear
B)
500 done
clear
C)
300 done
clear
D)
100 done
clear
View Solution play_arrow
-
question_answer35)
A roll of thread 907i cm long is cut into 5 parts to make up 5 circles as shown in the figure.
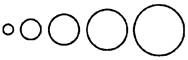
The radii of the circles increase by 1 cm consecutively. Find the radius of the smallest circle.
A)
7 cm done
clear
B)
5 cm done
clear
C)
6 cm done
clear
D)
9 cm done
clear
View Solution play_arrow
-
question_answer36)
A circle is divided into 18 sectors such that the angles subtended at the centre form an arithmetic progression. Given that the angle of the smallest sector is\[\text{11}.\text{5}{}^\circ \], find the angle of the biggest sector.
A)
\[\text{3}0{}^\circ \] done
clear
B)
\[\text{15}.\text{5}{}^\circ \] done
clear
C)
\[\text{45}{}^\circ \] done
clear
D)
\[\text{28}.\text{5}{}^\circ \] done
clear
View Solution play_arrow
-
question_answer37)
An arithmetic progression has 10 terms. The sum of the odd terms is 245 whereas the sum of the even terms is 305. Find the common difference.
A)
2 done
clear
B)
7 done
clear
C)
3 done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer38)
Given an arithmetic progression -10,-5,0,..... Identify three consecutive terms of the progression whose sum is 90.
A)
26, 31, 36 done
clear
B)
25, 30, 35 done
clear
C)
20, 30, 40 done
clear
D)
18, 23, 28 done
clear
View Solution play_arrow
-
question_answer39)
The first three terms of a sequence are 8, 'y' and 18. Find the positive value of 'y' so that the sequence is an arithmetic progression.
A)
26 done
clear
B)
18 done
clear
C)
12 done
clear
D)
13 done
clear
View Solution play_arrow
-
question_answer40)
The sum of the first 10 terms of an arithmetic progression is four times the sum of its first five terms. Find the ratio of the first term to the common difference.
A)
1:4 done
clear
B)
4:1 done
clear
C)
2:1 done
clear
D)
1:2 done
clear
View Solution play_arrow
-
question_answer41)
How many numbers between 100 and 1000 are divisible by 7?
A)
7 done
clear
B)
128 done
clear
C)
132 done
clear
D)
127 done
clear
View Solution play_arrow
-
question_answer42)
Find the sum of 14 AM's between 5 and 8.
A)
91 done
clear
B)
89 done
clear
C)
90 done
clear
D)
85 done
clear
View Solution play_arrow
-
question_answer43)
If\[{{\text{1}}^{\text{3}}}+{{\text{2}}^{\text{3}}}+.....+{{\text{m}}^{\text{3}}}=\text{3}0\text{25}\], find m.
A)
12 done
clear
B)
10 done
clear
C)
17 done
clear
D)
12 done
clear
View Solution play_arrow
-
question_answer44)
If\[{{m}^{th}}\]term of an arithmetic progression is 'n' and\[{{n}^{th}}\]term is 'm', find its\[{{(m+n)}^{th}}\]term.
A)
0 done
clear
B)
\[\text{m}+\text{n}-\text{p}\] done
clear
C)
\[\text{m}+\text{n}\] done
clear
D)
\[\frac{mn}{m+n}\] done
clear
View Solution play_arrow
-
question_answer45)
The sum to 'n' natural numbers is \[{{S}_{1}}\] sum of the squares of 'n' natural numbers is \[{{S}_{2}}\] and sum of the cubes of 'n' natural numbers is \[{{S}_{3}}\] Which of the following is equal to \[9S_{2}^{2}\]?
A)
\[(1-8{{S}_{1}}){{S}_{2}}\] done
clear
B)
\[{{S}_{3}}(1+8{{S}_{1}})\] done
clear
C)
\[{{S}_{1}}(1+8{{S}_{2}})\] done
clear
D)
\[{{S}_{1}}(1-8{{S}_{3}})\] done
clear
View Solution play_arrow
-
question_answer46)
In an arithmetic progression if 7 times the 7th term is equal to 11 times the 11th term, find its 18th term.
A)
1 done
clear
B)
0 done
clear
C)
-1 done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer47)
Find the sum of the numbers in between 1 and 1000 which are divisible by 9.
A)
55944 done
clear
B)
54954 done
clear
C)
99994 done
clear
D)
99894 done
clear
View Solution play_arrow
-
question_answer48)
There are 'n' arithmetic means in between 'a' and 'b'. Find the common difference.
A)
\[\frac{b-a}{n+1}\] done
clear
B)
\[\frac{b+a}{n-1}\] done
clear
C)
\[\frac{b-a}{n-1}\] done
clear
D)
\[\frac{b+a}{n+1}\] done
clear
View Solution play_arrow
-
question_answer49)
What is the sum of 'n' arithmetic means between 'a' and 'b'?
A)
\[\frac{3}{2}(a+2b)\] done
clear
B)
\[\frac{n}{2}[a+b]\] done
clear
C)
\[\frac{n}{2}[a-b]\] done
clear
D)
\[\frac{n}{4}[a+b]\] done
clear
View Solution play_arrow
-
question_answer50)
Find the sum of\[\left( 1-\frac{1}{n} \right)+\left( 1-\frac{2}{n} \right)+\left( 1-\frac{3}{n} \right)....\]terms.
A)
\[\frac{n}{2}\] done
clear
B)
\[\frac{n-1}{2}\] done
clear
C)
\[\frac{n+1}{2}\] done
clear
D)
\[\frac{n(n+1)}{{{n}^{2}}}\] done
clear
View Solution play_arrow
-
question_answer51)
In an arithmetic progression, if\[{{\text{t}}_{\text{p}}}\text{=q},{{\text{t}}_{\text{q}}}=\text{p},\]find \[{{\text{t}}_{\text{pq}}}\].
A)
\[\text{p}+\text{q}-\text{pq}\] done
clear
B)
\[\text{p}+\text{q}\] done
clear
C)
\[~\text{p}-\text{q}+\text{pq}\] done
clear
D)
\[\text{pq}-\text{p}-\text{q}\] done
clear
View Solution play_arrow
-
question_answer52)
Find three numbers in arithmetic progression whose sum is 3 and product is-35.
A)
\[\text{1},\text{5},\text{7}\] done
clear
B)
\[-\text{5},\text{7},-\text{1}\] done
clear
C)
\[-\text{5},\text{1},\text{7}\] done
clear
D)
\[-\text{7},\text{5},-\text{1}\] done
clear
View Solution play_arrow
-
question_answer53)
Which of the following is incorrect?
A)
\[{{S}_{n}}\]of the arithmetic progression 3, \[13,23,....\]is\[5{{n}^{2}}-8n\]. done
clear
B)
\[{{S}_{n}}=3{{n}^{2}}-8n\]is the sum of an arithmetic progression whose common difference is 6. done
clear
C)
\[{{n}^{th}}\]term, \[{{t}_{n}}={{s}_{n}}-{{s}_{n-1}}\] done
clear
D)
The\[{{n}^{th}}\]term of an arithmetic progression is \[{{t}_{n}}=a+(n-1)d\]. done
clear
View Solution play_arrow
-
question_answer54)
Given P=3+5+7+ .... (n terms) and Q = 5 + 8 +11 +..... (10 terms).What is the value of 'n' if\[\frac{P}{Q}=7\]?
A)
25 done
clear
B)
35 done
clear
C)
30 done
clear
D)
20 done
clear
View Solution play_arrow
-
question_answer55)
What is the value of 'x' if\[2x,x+10\]and\[3x+2\]are in arithmetic progression?
A)
5 done
clear
B)
6 done
clear
C)
4 done
clear
D)
-6 done
clear
View Solution play_arrow
