-
question_answer1)
A point on the line \[3x+5y=15\] and equidistant from the coordinate axes, lies in
A)
None of the quadrants done
clear
B)
Quadrants I and II only done
clear
C)
Quadrant I only done
clear
D)
Quadrants I, II, and III only done
clear
View Solution play_arrow
-
question_answer2)
If the lines \[y={{m}_{1}}x+c\]and \[y={{m}_{2}}x+{{c}_{2}}\]are parallel, then
A)
\[{{m}_{1}}={{m}_{2}}\] done
clear
B)
\[{{m}_{1}}{{m}_{2}}=1\] done
clear
C)
\[{{m}_{1}}{{m}_{2}}=-1\] done
clear
D)
\[{{m}_{1}}={{m}_{2}}=0\] done
clear
View Solution play_arrow
-
question_answer3)
If the coordinates of opposite vertices of a square are (1, 3) and (6, 0), the length of a side a square is
A)
\[\sqrt{34}\] done
clear
B)
\[\sqrt{17}\] done
clear
C)
17 done
clear
D)
12 done
clear
View Solution play_arrow
-
question_answer4)
The distance between the points A(-6, 7) and\[\text{B}\left( -\text{l},-\text{5} \right)\]is
A)
13 units done
clear
B)
14 units done
clear
C)
15 units done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer5)
If the distance between the points (k, - 1) and (3, 2) is 5, then the value of k is
A)
2 done
clear
B)
- 2 done
clear
C)
- 1 done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer6)
What points on the \[x\]-axis are at a distance of 5 units from the point \[\left( \text{5},-\text{4} \right)\] ?
A)
(2, 0) and (8, 0) done
clear
B)
(2, 1), (8, 1) done
clear
C)
(-2, 0) (-8, 0) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer7)
The area of a square whose vertices are (0, 2), (3, 1) (0, 4) and \[\left( \text{-3},1 \right)\] is
A)
\[\sqrt{18}\] sq. units done
clear
B)
18 sq. units done
clear
C)
15 sq. units done
clear
D)
\[\sqrt{15}\] sq. units done
clear
View Solution play_arrow
-
question_answer8)
The area of rectangles whose vertices are (0,1), (6, 7), \[\left( \text{-2},\text{ 3} \right)\]and (8, 3) is
A)
\[10\sqrt{5}\]sq. units done
clear
B)
\[\sqrt{5}\]sq. units done
clear
C)
40 sq. units done
clear
D)
\[\sqrt{15}\]sq. units done
clear
View Solution play_arrow
-
question_answer9)
The angle between \[y=x+4\]and\[y=2x-6\]is
A)
\[{{\tan }^{-1}}\frac{2}{3}\] done
clear
B)
\[{{\tan }^{-1}}\frac{3}{5}\] done
clear
C)
\[{{\tan }^{-1}}\frac{1}{2}\] done
clear
D)
\[{{\tan }^{-1}}\frac{1}{3}\] done
clear
View Solution play_arrow
-
question_answer10)
If the distance between (8, 0) and A is 7, then coordinates of the point A can not be
A)
(8,-7) done
clear
B)
(8,7) done
clear
C)
(1,0) done
clear
D)
(0,-8) done
clear
View Solution play_arrow
-
question_answer11)
If the points (0, 4) (4, 0) and (5, p) are collinear, then value of p is
A)
- 1 done
clear
B)
7 done
clear
C)
6 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer12)
The ordinate of the point which divides the line joining the origin and the point (1, 2) externally in the ratio of 3 : 2 is
A)
- 2 done
clear
B)
\[\frac{3}{5}\] done
clear
C)
\[\frac{2}{5}\] done
clear
D)
6 done
clear
View Solution play_arrow
-
question_answer13)
The centre of the circle passing through the points (5, 7), (6, 6) and (2, - 2) is
A)
(2, - 3) done
clear
B)
(2, - 1) done
clear
C)
(2, 3) done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer14)
The radius of the above circle is
A)
5 units done
clear
B)
6 units done
clear
C)
7 units done
clear
D)
8 units done
clear
View Solution play_arrow
-
question_answer15)
If the two vertices of an equilateral Lriangle be (0, 0) and (3, \[\sqrt{3}\] ), then the co-ordinates of third vertex are
A)
\[(0,2\sqrt{3})\,or\,(3,-\sqrt{3})\] done
clear
B)
\[(0,\sqrt{3})\,or\,(3,\sqrt{3})\] done
clear
C)
\[(0,2)\,(0,3)\] done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer16)
If A is a point on the y-axis whose ordinate is 5 and B is the point (-3, 1), then the length of AB is
A)
8 units done
clear
B)
5 units done
clear
C)
3 units done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer17)
The distance between two parallel lines \[3x+4y+10=0\] and \[3x+4y-10=0\] is
A)
0 done
clear
B)
\[-4\sqrt{5}\] done
clear
C)
\[2\sqrt{5}\] done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer18)
The line joining (- 1, 0) and (-2,\[-\sqrt{3}\] ) makes with the x-axis an angle equal to
A)
\[30{}^\circ \] done
clear
B)
\[45{}^\circ \] done
clear
C)
\[60{}^\circ \] done
clear
D)
\[75{}^\circ \] done
clear
View Solution play_arrow
-
question_answer19)
The graphs of\[2x+3y-6=0,4x-3y-6=0,\] \[x=2\] and \[y=\frac{2}{3}\] intersect in
A)
four points done
clear
B)
one point done
clear
C)
in no points done
clear
D)
infinite number of points done
clear
View Solution play_arrow
-
question_answer20)
X is a point out side of a circle whose centre is O. From X a tangent whose length is a, is drawn to the circle and the shortest distance from X to the circle is \[\frac{a}{2}\]. Find the radius of the circle.
A)
\[\frac{3a}{4}\] done
clear
B)
\[\frac{3a}{2}\] done
clear
C)
\[\frac{1}{2}a\] done
clear
D)
\[a\] done
clear
View Solution play_arrow
-
question_answer21)
The value of k when the distance between the points (3, k) and (4, 1) is \[\sqrt{10}\] is
A)
3 or 4 done
clear
B)
- 4 or - 2 done
clear
C)
- 4 or 2 done
clear
D)
4 or - 2 done
clear
View Solution play_arrow
-
question_answer22)
The length of a line segment is of 10 units and the co-ordinates of one end points are (2, - 3). If the abscissa of the other end is 10, then the ordinate of the other end is
A)
3 or -9 done
clear
B)
3 or 9 done
clear
C)
-3 or 9 done
clear
D)
-3 or -9 done
clear
View Solution play_arrow
-
question_answer23)
The point(s) on the ^y-axis that are at a distance of 10 units from the point (8, 8) are
A)
(0, - 2) and (0, - 14) done
clear
B)
(0, 2) and (0, 14) done
clear
C)
(0, 2) and (O, - 14) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer24)
The slope of the line joining the points (-8, - 3) and (8, 3) is
A)
\[\frac{8}{3}\] done
clear
B)
\[\frac{3}{8}\] done
clear
C)
0 done
clear
D)
- 1 done
clear
View Solution play_arrow
-
question_answer25)
The distance of the origin from the point of intersection of \[x+y=11\] and \[x-y-3=\] is
A)
7 done
clear
B)
14 done
clear
C)
\[\sqrt{65}\] done
clear
D)
\[\sqrt{33}\] done
clear
View Solution play_arrow
-
question_answer26)
What are the coordinates of the point of intersection of the two axes?
A)
(1,1) done
clear
B)
(0,0) done
clear
C)
(-1,1) done
clear
D)
(-1,-1) done
clear
View Solution play_arrow
-
question_answer27)
The area of the right angled \[\Delta \text{AOB}\]is 16 sec units If 0 is the origin and the coordinates of A are (8, 0), what are the coordinates of B?
A)
(0,4) done
clear
B)
(0,2) done
clear
C)
\[\left( -1,1 \right)\] done
clear
D)
\[\left( 0,\frac{1}{2} \right)\] done
clear
View Solution play_arrow
-
question_answer28)
The centre of the circle passing through the points (8, 12), (11, 3) and (0, 14) is
A)
(2, 5) done
clear
B)
(-2, 5) done
clear
C)
(3, 5) done
clear
D)
(4, 6) done
clear
View Solution play_arrow
-
question_answer29)
The equation of the straight line which is perpendicular to \[7x-8y=6\] is
A)
\[8x\text{ }+\text{ 7y }=\text{ 3}\] done
clear
B)
\[7x+8\text{y}=\text{3}\] done
clear
C)
\[8x-\text{7y}=\text{3}\] done
clear
D)
\[7x-8\text{y}=\text{3}\] done
clear
View Solution play_arrow
-
question_answer30)
If (0, 0), (3, 0) and (x, :y) are the vertices of an equilateral triangle, then the value of x and\[\text{y}\] is
A)
\[\left( \frac{3}{2},\frac{3\sqrt{3}}{2} \right)or\left( \frac{3}{2},\frac{-3\sqrt{3}}{2} \right)\] done
clear
B)
\[\left( \frac{1}{2},\sqrt{2} \right)or\left( \frac{1}{2},-\sqrt{2} \right)\] done
clear
C)
\[\left( \frac{1}{3},1 \right)or\left( \frac{1}{3},-1 \right)\] done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer31)
The vertices of a triangle are (-2, 0), (2, 3) and (1, - 3), then the type of the triangle is
A)
scalene done
clear
B)
equilateral done
clear
C)
isosceles done
clear
D)
right triangle done
clear
View Solution play_arrow
-
question_answer32)
The co-ordinates of a point R which divides the line joining A(-3, 3) and B(2, - 7) internally in the ratio 2 : 3 are
A)
(1,1) done
clear
B)
(-1,-1) done
clear
C)
(2,-2) done
clear
D)
(3,3) done
clear
View Solution play_arrow
-
question_answer33)
If the straight lines \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] at \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]are perpendicular to each other, then
A)
\[{{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}=0\] done
clear
B)
\[{{a}_{1}}{{a}_{2}}-{{b}_{1}}{{b}_{2}}=0\] done
clear
C)
\[{{a}_{1}}{{b}_{2}}+{{a}_{2}}{{b}_{1}}=0\] done
clear
D)
\[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}=0\] done
clear
View Solution play_arrow
-
question_answer34)
From P a line parallel to y-axis is drawn and from Q a line parallel to x-axis is drawn. Both these lines intersect at the point R. If the coordinates of P and Q are (3, 4) and (1, - 7), then find the coordinates of R.
A)
(3, 7) done
clear
B)
(3, - 7) done
clear
C)
\[\left( \text{l},-\text{4} \right)\] done
clear
D)
\[\left( \text{l},\text{4} \right)\] done
clear
View Solution play_arrow
-
question_answer35)
The co-ordinates of the point of trisection of the line segment joining the points (- 4, 3) and (2, - 1) are
A)
(2, 1) done
clear
B)
(3, 1) done
clear
C)
(-2,-\[\frac{5}{3}\]) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer36)
A point R(2, - 5) divides the line segment joining the point A(- 3, 5) and B(4, - 9), then the ratio is
A)
5 : 2 done
clear
B)
5 : 1 done
clear
C)
2 : 5 done
clear
D)
3 : 2 done
clear
View Solution play_arrow
-
question_answer37)
If (2, 1), (4, 5), (-1, - 3) are the mid points of the sides of a triangle, then the co-ordinates of its vertices are
A)
\[\left( -\text{3},-\text{7} \right),\text{ }\left( \text{17},\text{ 9} \right),\text{ }\left( \text{1},\text{1} \right)\] done
clear
B)
\[\left( -\text{3}.\text{ 7} \right),\text{ }\left( \text{7},\text{ 9} \right),\text{ }\left( -\text{ 1},\text{ 1} \right)\] done
clear
C)
\[\left( -\text{3},-\text{7} \right),\text{ }\left( \text{7},\text{ 9} \right),\text{ }\left( \text{1},\text{1} \right)\] done
clear
D)
none done
clear
View Solution play_arrow
-
question_answer38)
Two vertices of a triangle are (-1, 4) and (5, 2). If the centroid is (0, - 3), then the third vertex of the triangle is
A)
(- 4, - 15) done
clear
B)
(4, - 15) done
clear
C)
(-4, 15) done
clear
D)
(2 ,3) done
clear
View Solution play_arrow
-
question_answer39)
The ratio in which the line segment joining (3,4) and (--2,1) is divided by the y-axis is
A)
1: 2 done
clear
B)
1: 3 done
clear
C)
3:2 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer40)
The point which is equal-distant from the points (0, 0), (0, 8) and (4, 6) is
A)
\[\left( \frac{1}{2},-4 \right)\] done
clear
B)
\[\left( -\frac{1}{2},4 \right)\] done
clear
C)
\[\left( \frac{1}{2},4 \right)\] done
clear
D)
\[\left( -\frac{1}{2},-4 \right)\] done
clear
View Solution play_arrow
-
question_answer41)
The centroid of the triangle whose vertices are (4, - 8), (-9, 7) and (8,13) is
A)
(1, 4) done
clear
B)
(1,3) done
clear
C)
(1, 5) done
clear
D)
(1, 9) done
clear
View Solution play_arrow
-
question_answer42)
If mid point of the line segment joining (2a, 4) and \[\left( \text{-2},\text{3b} \right)\] is (1, 2a + 1), then the values of a and b are given by
A)
a = 2, b = - 2 done
clear
B)
a = b = 2 done
clear
C)
a = 1 = b done
clear
D)
a = -2, b = 2 done
clear
View Solution play_arrow
-
question_answer43)
The mid-point of the line segment AB is shown in the figure is (4, - 3). Then the co-ordinates of A and B are
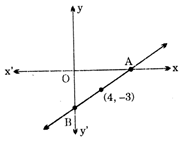
A)
(8, 0) and (0, - 6) done
clear
B)
(0, 8) and (0, - 6) done
clear
C)
(8, 0) and (-6, 0) done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer44)
If the coordinates of the vertices of a triangle are (0,0), (0, 2) and (3,1), then area of the triangle is
A)
3 sq. units done
clear
B)
- 3 sq. units done
clear
C)
2 sq. units done
clear
D)
1 sq. unit done
clear
View Solution play_arrow
-
question_answer45)
The coordinates of the vertices of a rectangle are (0, 0), (4, 0), (4, 3) and (0, 3). The length of its diagonal is
A)
4 done
clear
B)
5 done
clear
C)
7 done
clear
D)
3 done
clear
View Solution play_arrow
-
question_answer46)
If point P divides the line joining the points (5, 0) and (0, 4) in the ratio 2 : 3 internally, then the \[x\]-coordinate of P is
A)
2 done
clear
B)
1 done
clear
C)
3 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer47)
The gradient of the straight line \[3x+4y=5\]is
A)
\[\frac{3}{4}\] done
clear
B)
\[-\frac{4}{3}\] done
clear
C)
\[\frac{4}{3}\] done
clear
D)
\[-\frac{3}{4}\] done
clear
View Solution play_arrow
-
question_answer48)
The equation of the straight line which passes through the point (2, - 3) and makes an angle of \[\frac{\pi }{4}\]with the axis of \[x\]is
A)
\[~x-\text{ y }=\text{ 1}\] done
clear
B)
\[~x~-\text{y }=\text{ 5}\] done
clear
C)
\[~x\text{y }=\text{ 1}\] done
clear
D)
\[~x~+\text{ y }=\text{ 5}\] done
clear
View Solution play_arrow
-
question_answer49)
The equation of the straight line which is perpendicular to \[\text{7}x-\text{ 8y }=\text{ 6}\] is
A)
\[8x+7\text{y }=3\] done
clear
B)
\[7x+8\text{y }=3\] done
clear
C)
\[8x-7\text{y }=3\] done
clear
D)
\[7x-8\text{y }=3\] done
clear
View Solution play_arrow
-
question_answer50)
The length of the line segment whose end points are (3,-1) and (6, 5) is
A)
3 done
clear
B)
5 done
clear
C)
\[3\sqrt{5}\] done
clear
D)
\[5\sqrt{3}\] done
clear
View Solution play_arrow
-
question_answer51)
In the given figure co-ordinates of the midpoint of AB are
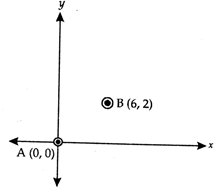
A)
(0, 2) done
clear
B)
(0,3) done
clear
C)
(1' 2) done
clear
D)
(3, 1) done
clear
View Solution play_arrow
-
question_answer52)
Slope of the line that passes through points (0, -2) and (3, 0) is
A)
\[-\frac{3}{2}\] done
clear
B)
\[-\frac{2}{3}\] done
clear
C)
0 done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer53)
In the given figure, if 0, P, Q, and R are the vertices of a square and the co-ordinates of P are (k, p), the values of k and p are
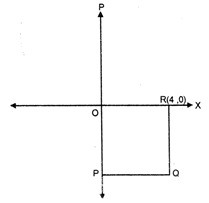
A)
k = - 4 and p = 0 done
clear
B)
k = 0 and p = - 4 done
clear
C)
k = -2 and p = 0 done
clear
D)
k = 0 and p = -2 done
clear
View Solution play_arrow
-
question_answer54)
Which of the following is a point on the graph of \[3x-2y=4?\]
A)
(0, 2) done
clear
B)
\[\left( \text{1},\text{ 4} \right)\] done
clear
C)
(2, 0) done
clear
D)
\[\left( \text{2},\text{ 1} \right)\] done
clear
View Solution play_arrow
-
question_answer55)
The slope of the line shown in the given figure
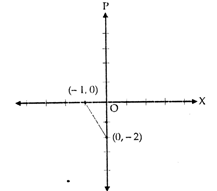
A)
2 done
clear
B)
1 done
clear
C)
-1 done
clear
D)
- 2 done
clear
View Solution play_arrow
-
question_answer56)
In the given figure, if AB is a diameter of circle P then perimeter of the shaded region is
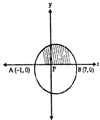
A)
\[4\pi +8\] done
clear
B)
\[8\pi +4\] done
clear
C)
\[8\pi +8\] done
clear
D)
\[16\pi +4\] done
clear
View Solution play_arrow
-
question_answer57)
If the line whose equation is \[y=x+2k\] passes through point (1, -3), then k is equal to
A)
-2 done
clear
B)
-1 done
clear
C)
1 done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer58)
Area of the rectangle whose vertices are (-2 5) (8, 5), (8,-2) and (-2,-2) is
A)
45 done
clear
B)
50 done
clear
C)
55 done
clear
D)
70 done
clear
View Solution play_arrow
-
question_answer59)
In the given figure, which of the following points lies within the circle?
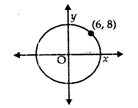
A)
(3.5, 9.5) done
clear
B)
\[(-7,7)\] done
clear
C)
(-10,1) done
clear
D)
\[(-10,1)\] done
clear
View Solution play_arrow
-
question_answer60)
The area of a parallelogram, whose vertices are (-4, -2), (-2, 6), (10, 6) and (8, -2) is
A)
32 done
clear
B)
48 done
clear
C)
72 done
clear
D)
96 done
clear
View Solution play_arrow
-
question_answer61)
Which of the following lines has the same Y -intercept as \[y=\frac{x}{2}-3\]?
A)
\[\text{x }+\text{ 2 }=\text{ 3y}\] done
clear
B)
\[\text{y}+\text{3}=\text{x}+\text{2}\] done
clear
C)
\[\text{y}+\text{3}=\text{2x}\] done
clear
D)
\[\frac{\text{y}}{2}=\text{x-3}\] done
clear
View Solution play_arrow
-
question_answer62)
In the given figure, if the slope of line 1 is m, then m in terms of h is
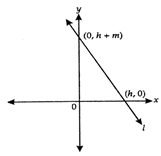
A)
\[\frac{h}{1+h}\] done
clear
B)
\[\frac{-h}{1+h}\] done
clear
C)
\[\frac{h}{1-h}\] done
clear
D)
\[1+h\] done
clear
View Solution play_arrow
-
question_answer63)
Slope of the line that is perpendicular to the line whose equation\[~\text{4x }+\text{ 5y }=\text{ 14}\], is
A)
\[-\frac{4}{5}\] done
clear
B)
\[\frac{5}{4}\] done
clear
C)
\[\frac{4}{5}\] done
clear
D)
\[-\frac{5}{4}\] done
clear
View Solution play_arrow
-
question_answer64)
The area of a triangle whose vertices are (-4, 0), (2, 4) and (4, 0) is
A)
8 done
clear
B)
12 done
clear
C)
16 done
clear
D)
32 done
clear
View Solution play_arrow
-
question_answer65)
If A (-3, 0) and C (5, 2) are the end points of diagonal AC of rectangle ABCD, with B on the x- axis, the perimeter of the rectangle ABCD is
A)
20 done
clear
B)
24 done
clear
C)
28 done
clear
D)
30 done
clear
View Solution play_arrow
-
question_answer66)
Area of the circle shown with its center at origin is
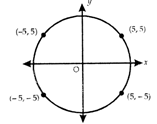
A)
\[5\,\pi \] done
clear
B)
\[15\,\pi \] done
clear
C)
\[25\,\pi \] done
clear
D)
\[50\,\pi \] done
clear
View Solution play_arrow
-
question_answer67)
If points A (2, 0) and B (8, -4) are the end points of diameter AB of circle 0, then area of circle 0 is
A)
\[10\,\pi \] done
clear
B)
\[13\,\pi \] done
clear
C)
\[24\,\pi \] done
clear
D)
\[26\,\pi \] done
clear
View Solution play_arrow
-
question_answer68)
In the figure given, area of the shaded region is
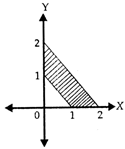
A)
1 done
clear
B)
\[\frac{3}{2}\] done
clear
C)
2 done
clear
D)
\[\frac{5}{2}\] done
clear
View Solution play_arrow
-
question_answer69)
A circle that has its center at the origin and passes through (-8, -6) will also pass through the point
A)
(1, 10) done
clear
B)
(4, 7) done
clear
C)
(7,7) done
clear
D)
(9, V19) done
clear
View Solution play_arrow
-
question_answer70)
In the given figure, ABC is a semi-circle with its center as origin. What is the area of AOPC?
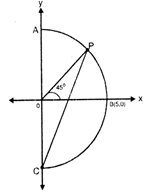
A)
\[\frac{25}{4}\] done
clear
B)
\[\frac{25}{4}(\sqrt{2}+1)\] done
clear
C)
\[\frac{25}{2\sqrt{2}}\] done
clear
D)
\[\frac{25}{2}\] done
clear
View Solution play_arrow
-
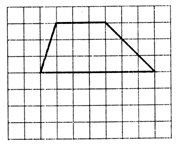
question_answer71)
In the given figure, the grid consists of unit squares. What is the area of the polygon?
A)
7 done
clear
B)
9 done
clear
C)
12 done
clear
D)
15 done
clear
View Solution play_arrow
-
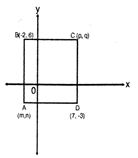
question_answer72)
Which of the following is an equation of the line that contains diagonal AC of square of ABCD shown in the figure?
A)
\[y=2x+1\] done
clear
B)
\[y=x+1\] done
clear
C)
\[y=\frac{1}{2}x-2\] done
clear
D)
\[y=x-1\] done
clear
View Solution play_arrow
-
question_answer73)
A circle whose center is at (-6, 8) passes through the origin which of the following points are not on the circle?
A)
(-2, 12) done
clear
B)
\[(-16,8)\] done
clear
C)
(-6,-2) done
clear
D)
(4 , 8) done
clear
View Solution play_arrow
-
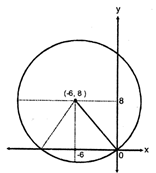
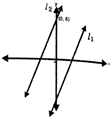
question_answer74)
The equation of line \[{{l}_{1}}\] is \[y=2x-4\]Line \[{{l}_{2}}\] parallel to line \[{{l}_{1}}\], and passes through point (0,6) is Which of the following is the equation of line \[{{l}_{2}}\]
A)
\[y=2x+6\] done
clear
B)
\[y=2x-6\] done
clear
C)
\[y=2x+3\] done
clear
D)
\[y=2x+4\] done
clear
View Solution play_arrow
-
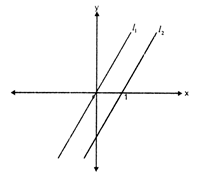
question_answer75)
In the rectangular co-ordinate system above, if the equation of \[{{l}_{1}}\] is y = x and parallel to \[{{l}_{2}}\], the shortest distance between \[{{l}_{1}}\] and \[{{l}_{2}}\]is
A)
\[\sqrt{2}\] done
clear
B)
1 done
clear
C)
\[\frac{\sqrt{2}}{2}\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow






