-
question_answer1)
What is the probability of getting a prime number in a throw of a die?
A)
2 done
clear
B)
\[\frac{1}{2}\] done
clear
C)
\[\frac{3}{2}\] done
clear
D)
6 done
clear
View Solution play_arrow
-
question_answer2)
What is, the probability that a vowel selected at random in English alphabet is an "i"?
A)
\[\frac{1}{5}\] done
clear
B)
\[\frac{1}{26}\] done
clear
C)
\[\frac{1}{6}\] done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer3)
When two dice are thrown, what is the probability of always getting a number greater than 4 on the second dice?
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{36}\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer4)
What is the probability for a leap year to have 52 Mondays and 53 Sundays?
A)
\[\frac{1}{366}\] done
clear
B)
\[\frac{1}{52}\] done
clear
C)
\[\frac{2}{7}\] done
clear
D)
\[\frac{1}{7}\] done
clear
View Solution play_arrow
-
question_answer5)
Cm In a single throw of two dice, what is the probability of getting a sum of 10?
A)
\[\frac{1}{12}\] done
clear
B)
\[\frac{1}{36}\] done
clear
C)
\[\frac{1}{6}\] done
clear
D)
\[\frac{1}{8}\] done
clear
View Solution play_arrow
-
question_answer6)
Three letters, to each of which corresponds an addressed envelope are placed in the envelopes at random. What is the probability that all letters are placed in the right envelopes?
A)
\[\frac{1}{3}\] done
clear
B)
1 done
clear
C)
\[\frac{1}{6}\] done
clear
D)
0 done
clear
View Solution play_arrow
-
question_answer7)
From a normal pack of cards, a card is drawn at random. Find the probability of getting a jack or a king.
A)
\[\frac{2}{52}\] done
clear
B)
\[\frac{1}{52}\] done
clear
C)
\[\frac{2}{13}\] done
clear
D)
\[\frac{1}{26}\] done
clear
View Solution play_arrow
-
question_answer8)
Two numbers are chosen from 1 to 5. What is the probability for the two numbers to be consecutive?
A)
\[\frac{1}{5}\] done
clear
B)
\[\frac{2}{5}\] done
clear
C)
\[\frac{1}{10}\] done
clear
D)
\[\frac{2}{10}\] done
clear
View Solution play_arrow
-
question_answer9)
Two dice are thrown at a time. What is the probability that the difference of the numbers shown on the dice is 1?
A)
\[\frac{5}{18}\] done
clear
B)
\[\frac{1}{36}\] done
clear
C)
\[\frac{1}{6}\] done
clear
D)
\[\frac{1}{12}\] done
clear
View Solution play_arrow
-
question_answer10)
A bag contains 3 white and 5 red balls. If a ball is drawn at random, what is the probability that it is red?
A)
\[\frac{3}{8}\] done
clear
B)
\[\frac{5}{8}\] done
clear
C)
\[\frac{3}{15}\] done
clear
D)
\[\frac{5}{15}\] done
clear
View Solution play_arrow
-
question_answer11)
What is the probability of getting an even number when a die is rolled?
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{1}{36}\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
\[\frac{1}{12}\] done
clear
View Solution play_arrow
-
question_answer12)
OA card is drawn from a packet of 100 cards numbered 1 to 100. Find the probability of drawing a number which is a square.
A)
\[\frac{1}{10}\] done
clear
B)
\[\frac{9}{100}\] done
clear
C)
\[\frac{1}{100}\] done
clear
D)
\[\frac{2}{100}\] done
clear
View Solution play_arrow
-
question_answer13)
A book containing 100 pages is opened at random. What is the probability that a doublet page is found?
A)
\[\frac{9}{100}\] done
clear
B)
\[\frac{90}{100}\] done
clear
C)
\[\frac{10}{100}\] done
clear
D)
\[\frac{20}{100}\] done
clear
View Solution play_arrow
-
question_answer14)
If a coin is tossed twice, find the probability of getting at least one head.
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{3}{4}\] done
clear
D)
\[\frac{1}{8}\] done
clear
View Solution play_arrow
-
question_answer15)
Find the probability of getting a number greater than 2 or an even number in a single throw of a fair die.
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{2}{3}\] done
clear
C)
\[\frac{5}{6}\] done
clear
D)
\[\frac{3}{5}\] done
clear
View Solution play_arrow
-
question_answer16)
Find the probability that in a family of 3 children, there is at least one boy.
A)
\[\frac{3}{4}\] done
clear
B)
\[\frac{1}{8}\] done
clear
C)
\[\frac{4}{8}\] done
clear
D)
\[\frac{5}{8}\] done
clear
View Solution play_arrow
-
question_answer17)
What is the chance that a non-leap year contains 53 Saturdays?
A)
\[\frac{2}{7}\] done
clear
B)
\[\frac{1}{7}\] done
clear
C)
\[\frac{2}{365}\] done
clear
D)
\[\frac{1}{365}\] done
clear
View Solution play_arrow
-
question_answer18)
From a well shuffled pack of cards, one card is drawn at random. What is the probability that the card drawn is a king?
A)
\[\frac{12}{13}\] done
clear
B)
\[\frac{1}{13}\] done
clear
C)
\[\frac{3}{13}\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer19)
An unbiased coin is tossed. What is the probability that neither head nor tail turns up?
A)
1 done
clear
B)
\[\frac{1}{2}\] done
clear
C)
0 done
clear
D)
\[\frac{1}{3}\] done
clear
View Solution play_arrow
-
question_answer20)
A box contains 7 red, 3 white and 2 black balls, when a ball is picked at random from the box what is the probability that it is not red?
A)
\[\frac{1}{12}\] done
clear
B)
\[\frac{11}{12}\] done
clear
C)
\[\frac{7}{12}\] done
clear
D)
\[\frac{5}{12}\] done
clear
View Solution play_arrow
-
question_answer21)
An unbiased coin is tossed 5 times. What is the odds in favour of getting at least one tail?
A)
31 :1 done
clear
B)
1 :31 done
clear
C)
32:32 done
clear
D)
31 :32 done
clear
View Solution play_arrow
-
question_answer22)
A coin is tossed successively three times. What is the probability of getting exactly one head or two heads?
A)
\[\frac{3}{4}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{1}{3}\] done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer23)
Three of the six vertices of a regular hexagon are chosen at random. What is the probability that the triangle with these vertices is equilateral?
A)
\[\frac{1}{5}\] done
clear
B)
\[\frac{2}{5}\] done
clear
C)
\[\frac{1}{10}\] done
clear
D)
\[\frac{3}{10}\] done
clear
View Solution play_arrow
-
question_answer24)
A coin is tossed successively three times. What is the probability of getting exactly one head or two heads?
A)
\[\frac{3}{4}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{1}{3}\] done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer25)
If\[P(A)=\frac{1}{3},P(B)=\frac{1}{2}\]and A and B are mutually exclusive, find\[P(A'\cap B')\].
A)
\[\frac{5}{6}\] done
clear
B)
\[\frac{1}{6}\] done
clear
C)
\[\frac{1}{5}\] done
clear
D)
\[\frac{2}{5}\] done
clear
View Solution play_arrow
-
question_answer26)
The probability that A can win a race is\[\frac{3}{8}\] and the probability that B can win it is\[\frac{1}{6}\]. If both run in a race, what is the probability that one of them will win the race, assuming that both cannot win together?
A)
\[\frac{17}{24}\] done
clear
B)
\[\frac{15}{24}\] done
clear
C)
\[\frac{13}{24}\] done
clear
D)
\[\frac{11}{24}\] done
clear
View Solution play_arrow
-
question_answer27)
A chess piece is randomly selected from a box that contains all the pieces used in the game of chess. Identify the sample space of this experiment.
A)
{King, Queen, Bishop, Knight} done
clear
B)
1,2,3,4,5,6,7} done
clear
C)
{Bishop, Castle, King, Pawn, Queen, Knight} done
clear
D)
{King, Knight, Pawn, Ace, Queen, Castle, Bishop} done
clear
View Solution play_arrow
-
question_answer28)
A month is randomly selected from a year. An event X is defined as 'the month with 30 days'. Identify the number of outcomes of event X.
A)
1 done
clear
B)
B done
clear
C)
3 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer29)
A spinner is spun. What is the number of possible outcomes of the event that the arrow will stop in the sector with an odd number.
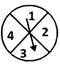
A)
1 done
clear
B)
2 done
clear
C)
3 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer30)
Turn the given cards facing down and shuffle.

Turn one card facing up. What is the probability that it shows a circle?
A)
\[\frac{2}{7}\] done
clear
B)
\[\frac{5}{7}\] done
clear
C)
\[\frac{3}{7}\] done
clear
D)
\[\frac{1}{7}\] done
clear
View Solution play_arrow
-
question_answer31)
A restaurant operator checked a sample of 200 plates and found that 10 of them were defective. The chef of the restaurant picks a plate from this sample. What is the probability that he will get a defective plate?
A)
0.5 done
clear
B)
0.05 done
clear
C)
0.2 done
clear
D)
20 done
clear
View Solution play_arrow
-
question_answer32)
Two dice are rolled at once and the numbers shown are added up. What is the probability of getting a total of 14?
A)
\[\frac{1}{2}\] done
clear
B)
1 done
clear
C)
0 done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer33)
The given figure shows 10 alphabet cards.

What is the probability of getting a card labelled 'S' when the card is chosen at random?
A)
\[\frac{1}{5}\] done
clear
B)
\[\frac{2}{5}\] done
clear
C)
\[\frac{1}{10}\] done
clear
D)
\[\frac{1}{6}\] done
clear
View Solution play_arrow
-
question_answer34)
A weather forecast center predicts that it will rain for 3 days in a duration of 20 days. Find the probability of rain on a particular day.
A)
\[\frac{17}{20}\] done
clear
B)
\[\frac{3}{17}\] done
clear
C)
\[\frac{20}{17}\] done
clear
D)
\[\frac{3}{20}\] done
clear
View Solution play_arrow
-
question_answer35)
90% of the mangoes in a bag are good. If a mango is chosen randomly from the box, find the probability of getting a bad mango.
A)
\[\frac{9}{100}\] done
clear
B)
\[\frac{1}{100}\] done
clear
C)
\[\frac{9}{10}\] done
clear
D)
\[\frac{1}{10}\] done
clear
View Solution play_arrow
-
question_answer36)
A fair coin is tossed thrice. Identify the probability of getting 3 tails as a fraction.
A)
\[\frac{1}{8}\] done
clear
B)
\[\frac{3}{8}\] done
clear
C)
\[\frac{7}{8}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer37)
The given figure shows two circles such that the radius of the small shaded circle is\[\frac{1}{3}\]. times the radius of the big circle. A dart is thrown randomly towards the circle. Find the probability that the dart hits the shaded target.

A)
\[\frac{1}{8}\] done
clear
B)
\[\frac{3}{8}\] done
clear
C)
\[\frac{7}{8}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer38)
7 marbles shown are kept in a tin.

If a marble is taken out randomly from the tin, state the probability that the marble has the number 2.
A)
\[\frac{2}{7}\] done
clear
B)
\[\frac{3}{7}\] done
clear
C)
\[\frac{5}{7}\] done
clear
D)
\[\frac{4}{7}\] done
clear
View Solution play_arrow
-
question_answer39)
Two fair dice are thrown. Find the probability that both dice show different numbers.
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{5}{6}\] done
clear
C)
\[\frac{32}{36}\] done
clear
D)
\[\frac{29}{36}\] done
clear
View Solution play_arrow
-
question_answer40)
A box contains 24 coloured marbles. Eighteen of then are yellow and the rest are either red or blue. A marble is picked at random. Find the probability of picking an yellow marble.
A)
\[\frac{1}{4}\] done
clear
B)
\[\frac{3}{4}\] done
clear
C)
\[\frac{3}{8}\] done
clear
D)
\[\frac{1}{8}\] done
clear
View Solution play_arrow
-
question_answer41)
A certain class has 's' students. If a student is picked at random, the probability of picking a boy is\[\frac{8}{13}\]. If the class has 24 boys, what is the value of 's'?
A)
26 done
clear
B)
39 done
clear
C)
52 done
clear
D)
60 done
clear
View Solution play_arrow
-
question_answer42)
A box contains 60 pens which are blue inked or black-inked. If a pen is picked at random, the probability of picking a blue-inked pen is .What is the number of blue-inked pens in the box?
A)
32 done
clear
B)
48 done
clear
C)
30 done
clear
D)
24 done
clear
View Solution play_arrow
-
question_answer43)
A certain class has 45 students. If a student is picked at random, the probability of picking a prefect is\[\frac{1}{3}\]. How many students in the class are not prefects?
A)
60 done
clear
B)
15 done
clear
C)
30 done
clear
D)
70 done
clear
View Solution play_arrow
-
question_answer44)
A bag contains several coloured balls. 28 of them are red. If a ball is drawn at random, the probability of drawing a red ball is\[\frac{4}{9}\].\[x\]balls are added into the box. A ball is then drawn at random. If the probability of drawing a red ball is now\[\frac{1}{2}\],find the value of\[x\].
A)
4 done
clear
B)
6 done
clear
C)
5 done
clear
D)
7 done
clear
View Solution play_arrow
-
question_answer45)
A bag contains 40 coins, consisting of Rs. 2, Rs. 5 and Rs.10 denominations. If a coin is drawn at random, the probability of drawing a Rs. 2 coin is \[\frac{5}{8}\].lf\[x\]Rs. 2 coins are removed from the bag and then a coin is drawn at random, the probability of drawing a Rs. 2 coin is\[\frac{1}{2}\]. Find the value of\[x\].
A)
5 done
clear
B)
2 done
clear
C)
10 done
clear
D)
8 done
clear
View Solution play_arrow
-
question_answer46)
The given incomplete table shows the number of coins in a box.
| Coins | Rs. 1 | Rs. 2 | Rs. 5 | 10 | 50 p |
| Amount | 6 | 12 | 8 | 10 | ? |
If a coin is drawn at random. the probability of drawing a Rs. 2 coin is\[\frac{3}{10}\]. Find the probability of drawing a 50 p coin.
A)
\[\frac{1}{10}\] done
clear
B)
\[\frac{2}{10}\] done
clear
C)
\[\frac{1}{5}\] done
clear
D)
\[\frac{2}{15}\] done
clear
View Solution play_arrow
-
question_answer47)
A factory has 120 workers in January. 90 of them are female workers. In February, another 15 male workers were employed. A worker is then picked at random. Calculate the probability of picking a female worker.
A)
\[\frac{3}{4}\] done
clear
B)
\[\frac{4}{9}\] done
clear
C)
\[\frac{2}{3}\] done
clear
D)
\[\frac{1}{3}\] done
clear
View Solution play_arrow
-
question_answer48)
A box contains a number of marbles with serial number 18 to 38.A marble is picked at a random. Find the probability that it is a multiple of 3.
A)
\[\frac{3}{5}\] done
clear
B)
\[\frac{7}{20}\] done
clear
C)
\[\frac{3}{4}\] done
clear
D)
\[\frac{1}{3}\] done
clear
View Solution play_arrow
-
question_answer49)
A box contains 40 marbles of red and blue colour. If a marble is picked at random, the probability of picking a blue marble is\[\frac{3}{8}\]. Rana takes out one red marble and nine blue marbles and then picks a marble at random. Find the probability that it is a blue marble.
A)
\[\frac{4}{5}\] done
clear
B)
\[\frac{2}{5}\] done
clear
C)
\[\frac{7}{40}\] done
clear
D)
\[\frac{1}{3}\] done
clear
View Solution play_arrow
-
question_answer50)
Set\[P=\{x:5\le x\le 22,x\,\text{is an integer}\}\]. If an element from set P is picked at random, calculate the probability that it is a prime number.
A)
\[\frac{5}{18}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{7}{9}\] done
clear
D)
\[\frac{5}{6}\] done
clear
View Solution play_arrow
-
question_answer51)
A box contains 32 coloured marbles. Eight of them are red marbles and the rest are either blue or green marbles. A marble is drawn at random. Calculate the probability of drawing a marble which is not red in colour.
A)
\[\frac{2}{3}\] done
clear
B)
\[\frac{5}{8}\] done
clear
C)
\[\frac{3}{4}\] done
clear
D)
\[\frac{7}{16}\] done
clear
View Solution play_arrow
-
question_answer52)
A Suppose a die is dropped at random on the rectangular region as shown in the figure.
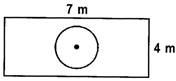
What is the probability that it will land inside the circle with diameter 2 m?
A)
\[\frac{\pi }{8}\] done
clear
B)
\[\frac{\pi }{28}\] done
clear
C)
\[\frac{1}{12}\] done
clear
D)
\[\frac{1}{18}\] done
clear
View Solution play_arrow
-
question_answer53)
A lottery has a 0.00002 probability of winning first prize. How many tickets have been sold for the lottery?
A)
2000 done
clear
B)
50000 done
clear
C)
2000 done
clear
D)
100000 done
clear
View Solution play_arrow
-
question_answer54)
250 tickets are sold for a raffle. A girl calculates that the tickets bought by her family give them a 0.032 probability of winning first prize. How many tickets did the family buy?
A)
60 done
clear
B)
9 done
clear
C)
50 done
clear
D)
8 done
clear
View Solution play_arrow
-
question_answer55)
All the three cards of spades are removed from a well-shuffled pack of 52 cards. A card is drawn at random from the remaining pack. Find the probability of getting a queen?
A)
\[\frac{3}{52}\] done
clear
B)
\[\frac{3}{49}\] done
clear
C)
\[\frac{1}{26}\] done
clear
D)
\[\frac{1}{52}\] done
clear
View Solution play_arrow
-
question_answer56)
A box contains 20 balls bearing numbers 1,2,3,...,20.A ball is drawn at random from the box. What is the probability that the number on the balls is not divisible by 10?
A)
\[\frac{9}{10}\] done
clear
B)
\[\frac{1}{10}\] done
clear
C)
\[\frac{9}{5}\] done
clear
D)
\[\frac{1}{5}\] done
clear
View Solution play_arrow
-
question_answer57)
A coin is tossed two times. Find the probability of getting a tail at least once.
A)
\[\frac{3}{4}\] done
clear
B)
\[\frac{2}{3}\] done
clear
C)
\[\frac{3}{5}\] done
clear
D)
\[\frac{1}{5}\] done
clear
View Solution play_arrow
-
question_answer58)
If a leap year is selected at random what is the probability that it will contain 53 Tuesdays?
A)
\[\frac{1}{7}\] done
clear
B)
\[\frac{2}{7}\] done
clear
C)
\[\frac{3}{7}\] done
clear
D)
\[\frac{4}{7}\] done
clear
View Solution play_arrow
-
question_answer59)
lf\[P(A\cup B)=0.65,P(A\cap B)=0.15,\]find \[P(\overline{A})+P(\overline{B})\].
A)
1.5 done
clear
B)
1.4 done
clear
C)
1.3 done
clear
D)
1.2 done
clear
View Solution play_arrow
-
question_answer60)
If the odds in favour of winning a race by three horses are respectively 1 : 4, 1 : 5 and 1 :6, find the probability that one of these horses will win.
A)
\[\frac{37}{60}\] done
clear
B)
\[\frac{39}{60}\] done
clear
C)
\[\frac{41}{60}\] done
clear
D)
\[\frac{51}{60}\] done
clear
View Solution play_arrow
-
question_answer61)
Two dice are rolled at once. What is the probability of getting an even number on the first die or a total of 8?
A)
\[\frac{4}{9}\] done
clear
B)
\[\frac{5}{9}\] done
clear
C)
\[\frac{7}{9}\] done
clear
D)
\[\frac{2}{9}\] done
clear
View Solution play_arrow
