question_answer 1)
Consider the following statements: The total energy of a particle executing simple harmonic motion depends on its:
(I) amplitude
(II) period
(III) displacement
Of these statements:
A)
\[\text{I}\] and \[\text{II}\] are correct
done
clear
B)
\[\text{II}\] and \[\text{III}\] are correct
done
clear
C)
\[\text{I}\] and \[\text{III}\] are correct
done
clear
D)
\[\text{I, II }and\,\text{III}\,are\,correct\]
done
clear
View Answer play_arrow
question_answer 2) The maximum velocity of a simple harmonic motion represented by \[y=3\sin \left( 100\,t+\frac{\pi }{6} \right)m\] is given by:
A)
300 m/s
done
clear
B)
\[\frac{\text{3}}{\text{6}}\text{m/s}\]
done
clear
C)
100 m/s
done
clear
D)
\[\frac{}{\text{6}}\text{m/s}\]
done
clear
View Answer play_arrow
question_answer 3) When earth moves round the sun, the quantity which remains constant is:
A)
angular velocity
done
clear
B)
kinetic energy
done
clear
C)
potential energy
done
clear
D)
areal velocity
done
clear
View Answer play_arrow
question_answer 4) 1 kg body explodes into three fragments. The ratio of their masses is 1:1:3. The fragments of same mass move perpendicular to each other with speeds 30 m/s, while the heavier part remains in the initial direction. The speed of heavier part is:
A)
\[\frac{10}{\sqrt{2}}\text{m/s}\]
done
clear
B)
\[\text{10}\sqrt{2\,}\text{m/s}\]
done
clear
C)
\[\text{20}\sqrt{2\,}\text{m/s}\]
done
clear
D)
\[\text{30}\sqrt{2\,}\text{m/s}\]
done
clear
View Answer play_arrow
question_answer 5) The dimensional formula for the gravitational constant is:
A)
\[\text{ }\!\![\!\!\text{ }{{\text{M}}^{\text{-1}}}{{\text{L}}^{\text{3}}}{{\text{T}}^{\text{-2}}}\text{ }\!\!]\!\!\text{ }\]
done
clear
B)
\[\text{ }\!\![\!\!\text{ ML}{{\text{T}}^{\text{-2}}}\text{ }\!\!]\!\!\text{ }\]
done
clear
C)
\[\text{ }\!\![\!\!\text{ M}{{\text{L}}^{2}}{{\text{T}}^{-2}}\text{ }\!\!]\!\!\text{ }\]
done
clear
D)
\[\text{ }\!\![\!\!\text{ }{{\text{M}}^{-1}}{{\text{L}}^{3}}\text{T }\!\!]\!\!\text{ }\]
done
clear
View Answer play_arrow
question_answer 6) A particle is moving in a circle of radius R with constant speed v. If radius is doubled, then its centripetal force to keep the same speed gets:
A)
twice as great as before
done
clear
B)
half
done
clear
C)
one-fourth
done
clear
D)
remains constant
done
clear
View Answer play_arrow
question_answer 7) If linear density of a rod of length 3 m varies as \[\lambda =2+x,\] then the position of the centre of gravity of the rod is:
A)
\[\frac{7}{3}m\]
done
clear
B)
\[\frac{12}{7}m\]
done
clear
C)
\[\frac{10}{7}m\]
done
clear
D)
\[\frac{9}{7}m\]
done
clear
View Answer play_arrow
question_answer 8) A block of mass m initially at rest is dropped from a height h on to a spring of force constant k. The maximum compression in the spring is x then:
A)
\[mgh=\frac{1}{2}k\,{{x}^{2}}\]
done
clear
B)
\[mg(h+x)=\frac{1}{2}k\,{{x}^{2}}\]
done
clear
C)
\[mgh=\frac{1}{2}k\,{{(x+h)}^{2}}\]
done
clear
D)
\[mg(h+x)=\frac{1}{2}k\,{{(x+h)}^{2}}\]
done
clear
View Answer play_arrow
question_answer 9) A ball of mass m moves with speed v and it strikes normally with a wall and reflected back normally. If its time of contact with wall is t, then find force exerted by ball on the wall.
A)
\[\frac{2mv}{t}\]
done
clear
B)
\[\frac{mv}{t}\]
done
clear
C)
\[mvt\]
done
clear
D)
\[\frac{mv}{2t}\]
done
clear
View Answer play_arrow
question_answer 10) A wheel of radius 1m rolls forward half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially in contact with the ground is :
A)
\[2\pi \]
done
clear
B)
\[\sqrt{2\pi }\]
done
clear
C)
\[\sqrt{{{\pi }^{2}}+4}\]
done
clear
D)
\[\pi \]
done
clear
View Answer play_arrow
question_answer 11) Water is flowing in a pipe of diameter 4 cm with a velocity 3 m/s. The water then enters into a pipe of diameter 2 cm. The velocity of water in the other pipe is:
A)
3 m/s
done
clear
B)
6 m/s
done
clear
C)
12 m/s
done
clear
D)
8 m/s
done
clear
View Answer play_arrow
question_answer 12) The surface tension of a liquid is 5 N/m. If a film is held on a ring of area \[0.02\,\,{{m}^{2}},\] its total surface energy is about:
A)
\[\text{2 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{J}\]
done
clear
B)
\[\text{2}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{J}\]
done
clear
C)
\[\text{2 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-1}}}\text{J}\]
done
clear
D)
\[\text{3 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-1}}}\text{J}\]
done
clear
View Answer play_arrow
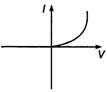
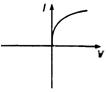
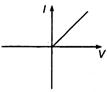
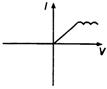
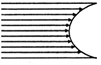
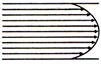
question_answer 13) A viscous fluid is flowing through a cylindrical tube. The velocity distribution of the fluid is best represented by the diagram:
A)
done
clear
B)
done
clear
C)
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 14) A wire is stretched by 1 mm by a force of 1 k N. The work done in stretching the wire is :
A)
5 erg
done
clear
B)
5 J
done
clear
C)
0.5 erg
done
clear
D)
0.5 J
done
clear
View Answer play_arrow
question_answer 15) In isochoric process:
A)
\[\Delta U=\Delta Q\]
done
clear
B)
\[\Delta Q=\Delta W\]
done
clear
C)
\[\Delta U=\Delta W\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 16) Which is not a path function?
A)
\[\Delta Q\]
done
clear
B)
\[\Delta Q+\Delta W\]
done
clear
C)
\[\Delta W\]
done
clear
D)
\[\Delta Q-\Delta W\]
done
clear
View Answer play_arrow
question_answer 17) The work done, V/during an isothermal process in which 1 mole of the gas expands from an initial volume \[{{V}_{1}}\] to a final volume \[{{V}_{2}}\] is given by: (R=gas constant, T= temperature)
A)
\[R({{V}_{2}}-{{V}_{1}}){{\log }_{e}}\left( \frac{{{T}_{1}}}{{{T}_{2}}} \right)\]
done
clear
B)
\[R({{T}_{2}}-{{T}_{1}}){{\log }_{e}}\left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)\]
done
clear
C)
\[RT{{\log }_{e}}\left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)\]
done
clear
D)
\[2RT{{\log }_{e}}\left( \frac{{{V}_{1}}}{{{V}_{2}}} \right)\]
done
clear
View Answer play_arrow
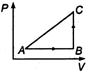
question_answer 18) The P-V diagram of a system undergoing thermodynamic transformation is shown in figure. The work done by the system in going from\[A\to B\to C\] is 30 J, and 40 J heat is given to the system. The change in internal energy between A and C is:
A)
10 J
done
clear
B)
70 J
done
clear
C)
84 J
done
clear
D)
134 J
done
clear
View Answer play_arrow
question_answer 19) The degrees of freedom of a molecule of a triatomic gas are:
A)
2
done
clear
B)
4
done
clear
C)
6
done
clear
D)
8
done
clear
View Answer play_arrow
question_answer 20) Ozone layer blocks the radiations of wave- length:
A)
less than \[\text{3 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-7}}}\text{m}\]
done
clear
B)
equal to \[\text{3 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-7}}}\text{m}\]
done
clear
C)
more than \[\text{3 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-7}}}\text{m}\]
done
clear
D)
all of the above
done
clear
View Answer play_arrow
question_answer 21) Two simple harmonic waves of the same amplitude and frequency differ by a phase\[\text{/2}\] When they are fed simultaneously to the X and Y-plates of a CRO, the screen would display the trace of:
A)
a circle
done
clear
B)
an ellipse
done
clear
C)
a straight line
done
clear
D)
a square
done
clear
View Answer play_arrow
question_answer 22) The speed of a wave is 360 m/s and frequency is 500 Hz. Phase difference between two consecutive particles is \[60{}^\circ \], then path difference between them will be:
A)
0.72 cm
done
clear
B)
120 cm
done
clear
C)
12 cm
done
clear
D)
7.2 cm
done
clear
View Answer play_arrow
question_answer 23) A string of length 2 m is fixed at both ends. If this string vibrates in its fourth normal mode with a frequency of 500 Hz, then the waves would travel on it with a velocity of:
A)
125 m/s
done
clear
B)
250 m/s
done
clear
C)
500 m/s
done
clear
D)
1000 m/s
done
clear
View Answer play_arrow
question_answer 24) The fundamental frequency of a sonometer wire is n. If its radius is doubled and its tension becomes half, the material of the wire remains same, the new fundamental frequency will be:
A)
\[n\]
done
clear
B)
\[\frac{n}{\sqrt{2}}\]
done
clear
C)
\[\frac{n}{2}\]
done
clear
D)
\[\frac{n}{2\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 25) In open organ pipe, if fundamental frequency is n, then the other frequencies are:
A)
n, 2 n, 3n, 4n
done
clear
B)
n, 3n, 5n
done
clear
C)
n, 2n, 4n, 8n
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 26) A sound wave of frequency \[f\] propagating through air with a velocity c, is reflected from a surface which is moving away from the source with a constant speed v. The frequency of the reflected wave, measured by the observer at the position of the source, is:
A)
\[\frac{f(c-v)}{c+v}\]
done
clear
B)
\[\frac{f(c+v)}{c-v}\]
done
clear
C)
\[\frac{f(c+2v)}{c+v}\]
done
clear
D)
\[\frac{f(c-v)}{c-2v}\]
done
clear
View Answer play_arrow
question_answer 27) A convex lens of focal length 10 cm and image formed by it, is at least distance of distinct vision then the magnifying power is:
A)
3.5
done
clear
B)
2.5
done
clear
C)
1.5
done
clear
D)
1.4
done
clear
View Answer play_arrow
question_answer 28) If two +5 D, lenses are mounted at some distance apart, the equivalent power will always be negative, if the distance is:
A)
greater than 40 cm
done
clear
B)
equal to 40 cm
done
clear
C)
equal to 10 cm
done
clear
D)
less than 10 cm
done
clear
View Answer play_arrow
question_answer 29) A Galilean telescope has an objective of focal length 100 cm and magnifying power 50. The distance between the two lenses in normal adjustment will be:
A)
98 cm
done
clear
B)
100 cm
done
clear
C)
150 cm
done
clear
D)
200 cm
done
clear
View Answer play_arrow
question_answer 30) A film projector magnifies a \[100\,c{{m}^{2}}\] film strip on a screen. If the linear magnification is 4, the area of the magnified film on the screen is:
A)
\[1600\,c{{m}^{2}}\]
done
clear
B)
\[400\,c{{m}^{2}}\]
done
clear
C)
\[800\,c{{m}^{2}}\]
done
clear
D)
\[200\,c{{m}^{2}}\]
done
clear
View Answer play_arrow
question_answer 31) The exposure time of a camera lens at\[f/2.8\] setting is 1/200 s. The correct exposure time at \[f/5.6\]setting is:
A)
0.02 s
done
clear
B)
0.04 s
done
clear
C)
0.20 s
done
clear
D)
0.40 s
done
clear
View Answer play_arrow
question_answer 32) In Youngs double slit experiment, the slit width and the distance of slits from the screen both are doubled. The fringe width:
A)
increases
done
clear
B)
decreases
done
clear
C)
remains unchanged
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 33) In Youngs double slit experiment, the aperture screen distance is 2 m. The slit width is 1 mm. Light of 600 nm is used. If a thin plate of glass \[(\mu =1.5)\] of thickness 0.06 mm is placed over one of the slits, then there will be a lateral displacement of the fringes by:
A)
zero
done
clear
B)
6 cm
done
clear
C)
10 cm
done
clear
D)
15 cm
done
clear
View Answer play_arrow
question_answer 34) A single slit is used to observe diffraction pattern with red light. on replacing the red light with violet light the diffraction pattern would:
A)
remain unchanged
done
clear
B)
become narrower
done
clear
C)
become broader
done
clear
D)
disappear
done
clear
View Answer play_arrow
question_answer 35) The resistance of a discharge tube is:
A)
zero
done
clear
B)
ohmic
done
clear
C)
non-ohmic
done
clear
D)
infinity
done
clear
View Answer play_arrow
question_answer 36) Which one of the following processes depends on gravity?
A)
Conduction
done
clear
B)
Convection
done
clear
C)
Radiation
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 37) The radius of solid metallic non-conducting sphere is 60 cm and charge on the sphere is \[500\,\mu C\]. The electric field at a distance 10 cm from centre of sphere is:
A)
\[2\times {{10}^{6}}\,N/C\]
done
clear
B)
\[2\times {{10}^{8}}\,N/C\]
done
clear
C)
\[5\times {{10}^{6}}\,N/C\]
done
clear
D)
\[5\times {{10}^{8}}\,N/C\]
done
clear
View Answer play_arrow
question_answer 38) The equivalent capacitance between the points A and B in the following circuit is:
A)
\[1\mu F\]
done
clear
B)
\[2\mu F\]
done
clear
C)
\[4\mu F\]
done
clear
D)
\[8\mu F\]
done
clear
View Answer play_arrow
question_answer 39) The figure shows a network of currents. The magnitude of current is shown here. The current \[I\] will be:
A)
3 A
done
clear
B)
9 A
done
clear
C)
13 A
done
clear
D)
19 A
done
clear
View Answer play_arrow
question_answer 40) If resistance of voltmeter is \[10000\,\Omega \] and resistance of galvanometer is \[2\,\,\Omega ,\] then find R when voltmeter reads 12 V and galvanometer reads 0.1 A.
A)
\[118\,\,\Omega \]
done
clear
B)
\[120\,\,\Omega \]
done
clear
C)
\[124\,\Omega \]
done
clear
D)
\[114\,\Omega \]
done
clear
View Answer play_arrow
question_answer 41) Two bulbs 25 W, 220 V and 100 W, 220 V are given. Which has higher resistance?
A)
25 W bulb
done
clear
B)
100 W bulb
done
clear
C)
Both bulbs will have equal resistance
done
clear
D)
Resistance of bulbs cannot be compared
done
clear
View Answer play_arrow
question_answer 42) An electron (mass \[9.1\times {{10}^{31}}\] kg, charge \[=1.6\times {{10}^{19}}C\]) experiences no deflection, if subjected to an electric field of \[3.2\times {{10}^{5}}V/m,\] and a magnetic field of \[2.0\times {{10}^{3}}\] \[Wb/{{m}^{2}}\]. Both the fields are normal to the path of electron and to each other. If the electric field is removed, then the electron will revolve in an orbit of radius:
A)
45 m
done
clear
B)
4.5 m
done
clear
C)
0.45 m
done
clear
D)
0.045 m
done
clear
View Answer play_arrow
question_answer 43) An LCR circuit of R = 100 0 is connected to an AC source 100 V, 50 Hz. The magnitude of phase difference between current and voltage is \[30{}^\circ \]. The power dissipated in the LCR circuit is:
A)
50 W
done
clear
B)
86.6 W
done
clear
C)
100 W
done
clear
D)
200 W
done
clear
View Answer play_arrow
question_answer 44) If half-life of radium is 77 days, its decay constant will be:
A)
\[\text{3 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{/day}\]
done
clear
B)
\[\text{9 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{/day}\]
done
clear
C)
\[\text{1 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{/day}\]
done
clear
D)
\[\text{6 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{/day}\]
done
clear
View Answer play_arrow
question_answer 45) In a radioactive reaction\[_{92}{{X}^{232}}{{\to }_{82}}{{X}^{204}}\] the number of \[\alpha \]-particles emitted is:
A)
7
done
clear
B)
6
done
clear
C)
5
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 46) According to Hubbles law, the red-shift (Z) of a receding galaxy and its distance r from aril are related as:
A)
\[Z\,\propto r\]
done
clear
B)
\[Z\,\propto \frac{1}{r}\]
done
clear
C)
\[Z\,\propto \frac{1}{{{r}^{2}}}\]
done
clear
D)
\[Z\,\propto {{r}^{3/2}}\]
done
clear
View Answer play_arrow
question_answer 47) The de-Broglie wavelength of a body of mass m and kinetic energy E is given by:
A)
\[\lambda =\frac{h}{mE}\]
done
clear
B)
\[\lambda =\frac{\sqrt{2mE}}{h}\]
done
clear
C)
\[\lambda =\frac{h}{2mE}\]
done
clear
D)
\[\lambda =\frac{h}{\sqrt{2mE}}\]
done
clear
View Answer play_arrow
question_answer 48) Different voltages are applied across a p-n junction and the currents are measured form each value. Which of die following graphs is obtained between voltage and current?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 49)
A logic gate having two inputs A and B and output C has the following truth table
A
B
C
1
1
0
1
0
1
0
1
1
0
0
1
It is :
A)
an OR gate
done
clear
B)
an AND gate
done
clear
C)
a NOR gate
done
clear
D)
a NAND gate
done
clear
View Answer play_arrow
question_answer 50) For sky wave propagation of 10 MHz signal, what should be the minimum electron density in ionosphere?
A)
\[\sim 1.2\times {{10}^{12}}{{m}^{-3}}\]
done
clear
B)
\[\sim {{10}^{6}}{{m}^{-3}}\]
done
clear
C)
\[\sim {{10}^{14}}{{m}^{-3}}\]
done
clear
D)
\[\sim {{10}^{22}}{{m}^{-3}}\]
done
clear
View Answer play_arrow
question_answer 51) The number of molecules of \[C{{O}_{2}}\]present in 44 g of \[C{{O}_{2}}\]is:
A)
\[6.0\times {{10}^{23}}\]
done
clear
B)
\[3\times {{10}^{23}}\]
done
clear
C)
\[12\times {{10}^{23}}\]
done
clear
D)
\[3\times {{10}^{10}}\]
done
clear
View Answer play_arrow
question_answer 52) Magnitude of kinetic energy in an orbit is equal to:
A)
half of the potential energy
done
clear
B)
twice of the potential energy
done
clear
C)
one fourth of the potential energy
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 53) A p-orbital in a given shell can accommodate upto:
A)
four electrons
done
clear
B)
two electrons with parallel spin
done
clear
C)
six electrons
done
clear
D)
two electrons with opposite spin
done
clear
View Answer play_arrow
question_answer 54) Which of the following is Heisenberg uncertainty principle?
A)
\[\Delta x.\Delta p\ge \frac{h}{4\pi }\]
done
clear
B)
\[\Delta x.\Delta p=\frac{h}{4\pi }\]
done
clear
C)
\[\Delta x.\Delta p\le \frac{h}{4\pi }\]
done
clear
D)
\[\Delta x.\Delta p<\frac{h}{4\pi }\]
done
clear
View Answer play_arrow
question_answer 55) Chromium is represented by the electronic configuration:
A)
\[\text{ }\!\![\!\!\text{ }Ne\text{ }\!\!]\!\!\text{ }3{{s}^{2}}\text{ }3{{P}^{6}}\text{ }3{{d}^{1}}\text{ }4{{s}^{2}}\]
done
clear
B)
\[\text{ }\!\![\!\!\text{ }Ne\text{ }\!\!]\!\!\text{ }3{{s}^{2}}\text{ }3{{p}^{6}}\text{ }3{{d}^{2}}\text{ }4{{s}^{1}}\]
done
clear
C)
\[\text{ }\!\![\!\!\text{ }Ne\text{ }\!\!]\!\!\text{ }3{{s}^{2}}\text{ }3{{p}^{6}}\text{ }3{{d}^{5}}\text{ }4{{s}^{1}}\]
done
clear
D)
\[~[Ne]\text{ }3{{s}^{2}}\text{ }3{{p}^{6}}\text{ }4{{s}^{2}}\text{ }3{{d}^{4}}\]
done
clear
View Answer play_arrow
question_answer 56) Number of neutron in \[{{C}^{12}}\]is:
A)
6
done
clear
B)
7
done
clear
C)
8
done
clear
D)
9
done
clear
View Answer play_arrow
question_answer 57) H-bond is not present in:
A)
water
done
clear
B)
glycerol
done
clear
C)
hydrogen fluoride
done
clear
D)
hydrogen sulphide.
done
clear
View Answer play_arrow
question_answer 58) Oxidation number of S in\[SO_{4}^{2-}:\]
A)
+ 6
done
clear
B)
+ 3
done
clear
C)
+ 2
done
clear
D)
- 2
done
clear
View Answer play_arrow
question_answer 59) 2 g of \[{{O}_{2}}\] at\[~27{{\,}^{o}}C\] and 760 mm of Hg pressure has volume:
A)
1.4 L
done
clear
B)
2.8 L
done
clear
C)
11.2 L
done
clear
D)
22.4 L
done
clear
View Answer play_arrow
question_answer 60) If pressure increases then its effect on given equilibrium \[2NO(g){{N}_{2}}(g)+{{O}_{2}}(g)\] is shift in:
A)
forward direction
done
clear
B)
backward direction
done
clear
C)
no effect
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 61) Which is Lewis base: \[{{I}_{2}}+{{I}^{-}}\xrightarrow{{}}{{I}_{3}}^{-}\]?
A)
\[{{I}_{2}}\]
done
clear
B)
\[I_{3}^{-}\]
done
clear
C)
\[{{I}^{-}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 62) The heat of neutralization of any strong acid and a strong base is nearly equal to:
A)
\[-75.3\,kJ\]
done
clear
B)
\[~+\,57.3\,kJ\]
done
clear
C)
\[-57.3\,kJ\]
done
clear
D)
\[+\,75.3\,kJ\]
done
clear
View Answer play_arrow
question_answer 63) pH of \[{{10}^{-8}}\,M\,HCl\]solution is:
A)
8
done
clear
B)
between 7 and 8
done
clear
C)
between 6 and 7
done
clear
D)
between 8 and 9
done
clear
View Answer play_arrow
question_answer 64) A reaction \[A\xrightarrow{{}}B\]follows a second order kinetic. Doubling the concentration of A will increase the rate of formation of B by a factor of:
A)
1/4
done
clear
B)
4
done
clear
C)
1/2
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 65) Which of the following is always negative for exothermic reaction?
A)
\[\Delta H\]
done
clear
B)
\[\Delta S\]
done
clear
C)
\[\Delta G\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 66) Unit of equivalent conductance is:
A)
\[oh{{m}^{-1}}\,c{{m}^{2}}\,{{(g-eq)}^{-1}}\]
done
clear
B)
\[ohm\,cm\,(g-eq)\]
done
clear
C)
\[ohm\,c{{m}^{2}}\,{{(g-eq)}^{-1}}\]
done
clear
D)
\[oh{{m}^{-1}}\,cm\,{{(g-eq)}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 67) For cell reaction \[Zn+C{{u}^{2+}}\xrightarrow{{}}Z{{n}^{2+}}+Cu\] cell representation is:
A)
\[Zn|Z{{n}^{2+}}||C{{u}^{2+}}|Cu\]
done
clear
B)
\[Cu|C{{u}^{2+}}||Z{{n}^{2+}}|Zn\]
done
clear
C)
\[Cu|Z{{n}^{2+}}||Zn|C{{u}^{2+}}\]
done
clear
D)
\[C{{u}^{2+}}|Zn||Z{{n}^{2+}}|Cu\]
done
clear
View Answer play_arrow
question_answer 68) Molal solution means 1 mole of solute present in:
A)
\[1000\,g\]of solvent
done
clear
B)
1 L of solvent
done
clear
C)
1 L of solution
done
clear
D)
\[1000\,g\]of solution
done
clear
View Answer play_arrow
question_answer 69) Which of the following shows maximum depression in freezing point?
A)
\[{{K}_{2}}S{{O}_{4}}\]
done
clear
B)
\[NaCl\]
done
clear
C)
Urea
done
clear
D)
Glucose
done
clear
View Answer play_arrow
question_answer 70) An emulsion is a colloidal dispersion of:
A)
a liquid in a gas
done
clear
B)
a liquid in a liquid
done
clear
C)
a solid in a liquid
done
clear
D)
a gas in a solid
done
clear
View Answer play_arrow
question_answer 71) Size of colloidal particle is:
A)
\[1\,nm\]
done
clear
B)
\[1-100\,nm\]
done
clear
C)
\[<\,100\,nm\]
done
clear
D)
\[>\,100\,nm\]
done
clear
View Answer play_arrow
question_answer 72) Ether show isomerism with:
A)
alcohol
done
clear
B)
ethane
done
clear
C)
halide
done
clear
D)
aldehyde
done
clear
View Answer play_arrow
question_answer 73) Which of the following shows geometrical isomerism?
A)
\[{{C}_{2}}{{H}_{5}}Br\]
done
clear
B)
\[(C{{H}_{2}}){{(COOH)}_{2}}\]
done
clear
C)
\[{{(CH)}_{2}}{{(COOH)}_{2}}\]
done
clear
D)
\[{{C}_{2}}{{H}_{6}}\]
done
clear
View Answer play_arrow
question_answer 74) Which of the following is present in natural gas?
A)
\[n-\]butane
done
clear
B)
Ethane
done
clear
C)
Methane
done
clear
D)
Propane
done
clear
View Answer play_arrow
question_answer 75) Which of the following have delocalized electron?
A)
Benzene
done
clear
B)
Cyclohexane
done
clear
C)
\[C{{H}_{4}}\]
done
clear
D)
\[{{C}_{2}}{{H}_{6}}\]
done
clear
View Answer play_arrow
question_answer 76) Nitration of benzene is:
A)
electrophilic substitution
done
clear
B)
electrophilic addition
done
clear
C)
nucleophilic substitution
done
clear
D)
nucleophilic addition
done
clear
View Answer play_arrow
question_answer 77) Alkyl halide can be converted into alkene by:
A)
nucleophilic substitution reaction
done
clear
B)
elimination reaction
done
clear
C)
both nucleophilic substitution and elimination reaction
done
clear
D)
rearrangement
done
clear
View Answer play_arrow
question_answer 78) Which of the following compounds is most acidic?
A)
\[C{{H}_{4}}\]
done
clear
B)
\[{{C}_{2}}{{H}_{6}}\]
done
clear
C)
\[CH\equiv CH\]
done
clear
D)
\[{{C}_{2}}{{H}_{5}}OH\]
done
clear
View Answer play_arrow
question_answer 79) Which of the following reacts with \[KMn{{O}_{4}}\]but does not react with\[AgN{{O}_{3}}\]?
A)
\[{{C}_{2}}{{H}_{6}}\]
done
clear
B)
\[C{{H}_{4}}\]
done
clear
C)
\[{{C}_{2}}{{H}_{4}}\]
done
clear
D)
\[{{C}_{2}}{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 80) Which of the following compound does not show anti-Markownikoffs addition?
A)
Propene
done
clear
B)
1-butene
done
clear
C)
2-butene
done
clear
D)
2-pentene
done
clear
View Answer play_arrow
question_answer 81) Methyl ketone is identified by:
A)
lodoform test
done
clear
B)
Fehling solution
done
clear
C)
Tollens reagent
done
clear
D)
Schiffs reagent
done
clear
View Answer play_arrow
question_answer 82) Which of the following does not give Fehling solution test?
A)
Acetone
done
clear
B)
Propanal
done
clear
C)
Ethanal
done
clear
D)
Butanal
done
clear
View Answer play_arrow
question_answer 83) Cyanide group on hydrolysis gives:
A)
acid
done
clear
B)
acetamide
done
clear
C)
amine
done
clear
D)
hydrate
done
clear
View Answer play_arrow
question_answer 84) In alkyl cyanide alkyl group attached with:
A)
C of CN group
done
clear
B)
N of CN group
done
clear
C)
either C or N of CN group
done
clear
D)
both C and N of CN group
done
clear
View Answer play_arrow
question_answer 85) Fat on hydrolysis gives which alcohol
A)
Glycerol
done
clear
B)
Propanol
done
clear
C)
Butanol
done
clear
D)
Ethanol
done
clear
View Answer play_arrow
question_answer 86) Which of the following is natural polymer?
A)
PVC
done
clear
B)
Nylon 66
done
clear
C)
Teflon
done
clear
D)
Cellulose
done
clear
View Answer play_arrow
question_answer 87) Condensation product of caprolactum is:
A)
Nylon 6
done
clear
B)
Nylon 66
done
clear
C)
Nylon 60
done
clear
D)
Nylon 6, 10
done
clear
View Answer play_arrow
question_answer 88) Which inert gas have highest boiling point
A)
\[Xe\]
done
clear
B)
\[Ar\]
done
clear
C)
Kr
done
clear
D)
He
done
clear
View Answer play_arrow
question_answer 89) In Ostwald process of manufacturing of \[\text{HN}{{\text{O}}_{\text{3}}}\text{,}\]catalyst used is:
A)
Mo
done
clear
B)
Fe
done
clear
C)
Mn
done
clear
D)
Pt
done
clear
View Answer play_arrow
question_answer 90) Important ore of Mg is:
A)
Gypsum
done
clear
B)
Camallite
done
clear
C)
Magnatide
done
clear
D)
Camolite
done
clear
View Answer play_arrow
question_answer 91) Purification of Al by electrolysis method is called:
A)
Halls process
done
clear
B)
Baeyer process
done
clear
C)
Ostwald process
done
clear
D)
Hoopes process
done
clear
View Answer play_arrow
question_answer 92) Decreasing size of ions is:
A)
\[\text{I}\,\text{}\,{{\text{I}}^{-}}>{{I}^{+}}\]
done
clear
B)
\[\text{I}{{\,}^{-}}\text{}\,\text{I}>{{I}^{+}}\]
done
clear
C)
\[\text{I}{{\,}^{+}}\text{}\,{{\text{I}}^{-}}>I\]
done
clear
D)
\[\text{I}\,\text{}\,{{\text{I}}^{+}}>{{I}^{-}}\]
done
clear
View Answer play_arrow
question_answer 93) Which of the following is kept in water?
A)
White phosphorus
done
clear
B)
Sodium
done
clear
C)
Potassium
done
clear
D)
Calcium
done
clear
View Answer play_arrow
question_answer 94) When heated\[N{{H}_{3}}\] is passed over\[CuO\]gas evolved is:
A)
\[{{N}_{2}}\]
done
clear
B)
\[{{N}_{2}}O\]
done
clear
C)
\[HN{{O}_{3}}\]
done
clear
D)
\[N{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 95) Formula of hypophosphorus acid is:
A)
\[H-\underset{H}{\overset{O}{\mathop{\underset{||}{\overset{||}{\mathop{P}}}\,}}}\,-OH\]
done
clear
B)
\[HO-\underset{OH}{\overset{O}{\mathop{\underset{||}{\overset{||}{\mathop{P}}}\,}}}\,-OH\]
done
clear
C)
\[H-\underset{H}{\overset{O}{\mathop{\underset{||}{\overset{||}{\mathop{P}}}\,}}}\,=OH\]
done
clear
D)
\[H-\underset{OH}{\overset{O}{\mathop{\underset{|}{\overset{||}{\mathop{P}}}\,}}}\,-OH\]
done
clear
View Answer play_arrow
question_answer 96) Most powerful reducing agent is:
A)
\[Li\]
done
clear
B)
\[Na\]
done
clear
C)
\[Ca\]
done
clear
D)
\[Mg\]
done
clear
View Answer play_arrow
question_answer 97) When calomel reacts with \[N{{H}_{4}}OH\]solution the compound formed is:
A)
\[N{{H}_{2}}-Hg-Cl\]
done
clear
B)
\[H{{g}_{2}}C{{l}_{2}}N{{H}_{3}}\]
done
clear
C)
\[Hg{{(N{{H}_{3}})}_{2}}C{{l}_{2}}\]
done
clear
D)
\[HgC{{l}_{2}}N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 98) Which of the following is colored compound?
A)
\[Cu{{F}_{2}}\]
done
clear
B)
\[CuI\]
done
clear
C)
\[NaCI\]
done
clear
D)
\[MgC{{l}_{2}}\]
done
clear
View Answer play_arrow
question_answer 99) \[{{H}_{2}}{{O}_{2}}\]is formed by which of the following compounds?
A)
\[N{{a}_{2}}{{O}_{2}}\]
done
clear
B)
\[NaOH\]
done
clear
C)
\[N{{a}_{2}}O\]
done
clear
D)
\[K{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 100) Copper sulphate solution reacts with KCN and gives:
A)
\[{{K}_{3}}[Cu{{(CN)}_{4}}]\]
done
clear
B)
\[CuCN\]
done
clear
C)
\[Cu{{(CN)}_{2}}\]
done
clear
D)
\[{{K}_{2}}[Cu{{(CN)}_{4}}]\]
done
clear
View Answer play_arrow
question_answer 101) If \[A\subseteq B,\]then \[B\cup A\]is equal to:
A)
\[B\cap A\]
done
clear
B)
A
done
clear
C)
B
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 102) The real value of \[\alpha \]for which the expression \[\frac{1-i\sin \alpha }{1+2i\,\sin \alpha }\] is purely real, is:
A)
\[(2n+1)\frac{\pi }{2}\]
done
clear
B)
\[(n+1)\frac{\pi }{2}\]
done
clear
C)
\[n\pi \]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 103) The medians AD and BE of the triangle with vertices A (0, b), B (0, 0) and C (a, 0) are mutually perpendicular, if:
A)
\[b=a\]
done
clear
B)
\[b=-2\sqrt{a}\]
done
clear
C)
\[a=\pm \sqrt{2b}\]
done
clear
D)
\[b=\sqrt{2}\,a\]
done
clear
View Answer play_arrow
question_answer 104) The equation of line parallel to the tangent to the circle \[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\]at the point \[({{x}_{1}},{{y}_{1}})\] and passing through origin, is:
A)
\[x{{y}_{1}}+{{x}_{1}}y=0\]
done
clear
B)
\[x{{x}_{1}}-y{{y}_{1}}=0\]
done
clear
C)
\[x{{x}_{1}}+y{{y}_{1}}=0\]
done
clear
D)
\[xy-{{x}_{1}}y=0\]
done
clear
View Answer play_arrow
question_answer 105) \[\sin {{200}^{o}}+\cos {{200}^{o}}\]is:
A)
positive
done
clear
B)
negative
done
clear
C)
zero
done
clear
D)
zero or positive
done
clear
View Answer play_arrow
question_answer 106) The principal value of \[{{\sin }^{-1}}\left( -\frac{\sqrt{3}}{2} \right)\]is:
A)
\[\frac{4\pi }{3}\]
done
clear
B)
\[\frac{5\pi }{3}\]
done
clear
C)
\[-\frac{2\pi }{3}\]
done
clear
D)
\[-\frac{\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 107) If \[xy+yz+zx=1,\]then \[\sum{\frac{x+y}{1-xy}}\]is equal to:
A)
\[\frac{4}{xyz}\]
done
clear
B)
\[\frac{1}{xyz}\]
done
clear
C)
\[~xyz\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 108) A vertical pole (more than 100 m high) consists of two portions, the lower being one-third of the whole. If the upper portion subtends an angle \[{{\tan }^{-1}}\frac{1}{2}\]at a point in a horizontal plane through the foot of the pole and distance 40 ft from it, then the height of the pole is:
A)
100 ft
done
clear
B)
120 ft
done
clear
C)
150 ft
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 109) When the three coins are tossed simultaneously, then the probability of getting one head will be:
A)
\[\frac{3}{7}\]
done
clear
B)
\[\frac{1}{7}\]
done
clear
C)
\[\frac{3}{8}\]
done
clear
D)
\[\frac{7}{8}\]
done
clear
View Answer play_arrow
question_answer 110) The cosine of the angle between any two diagonals of a cube is:
A)
\[\frac{1}{3}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\frac{2}{3}\]
done
clear
D)
\[\frac{1}{\sqrt{3}}\]
done
clear
View Answer play_arrow
question_answer 111) If\[f\]is any function, then \[\frac{1}{2}[f(x)+f(-x)]\]is always:
A)
odd
done
clear
B)
even
done
clear
C)
neither even nor odd
done
clear
D)
one-one
done
clear
View Answer play_arrow
question_answer 112) If \[f(x)=\log \left( \frac{1+x}{1-x} \right)\]and \[g(x)=\frac{3x+{{x}^{3}}}{1+3{{x}^{2}}},\]then \[f(g(x))\]is equal to:
A)
\[f(3x)\]
done
clear
B)
\[{{(f(x))}^{3}}\]
done
clear
C)
\[3f(x)\]
done
clear
D)
\[-f(x)\]
done
clear
View Answer play_arrow
question_answer 113) \[\underset{x\to 0}{\mathop{\lim }}\,[\cos x]\]is equal to:
A)
\[-1\]
done
clear
B)
1
done
clear
C)
0
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 114) \[\frac{d}{dx}({{\sin }^{-1}}2x\sqrt{1-{{x}^{2}}})\]is equal to:
A)
\[-\frac{2}{\sqrt{1-{{x}^{2}}}}\]
done
clear
B)
\[\frac{2}{\sqrt{1-{{x}^{2}}}}\]
done
clear
C)
\[cos\,2x\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 115) \[\int_{0}^{\pi /2}{|\sin x-\cos x|}\,dx\] is equal to:
A)
\[2(\sqrt{2}+1)\]
done
clear
B)
\[\sqrt{2}-1\]
done
clear
C)
\[2(\sqrt{2}-1)\]
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 116) If p and q are the roots of the equation \[{{x}^{2}}+pq=(p+1)x,\], then \[q\]is equal to:
A)
\[~-1\]
done
clear
B)
2
done
clear
C)
1
done
clear
D)
\[-2\]
done
clear
View Answer play_arrow
question_answer 117) If a line lies in the octant OXYZ and it makes equal angle with the axes, then:
A)
\[l=m=n=\frac{1}{\sqrt{3}}\]
done
clear
B)
\[l=m=n=\pm \frac{1}{\sqrt{3}}\]
done
clear
C)
\[l=m=n=-\frac{1}{\sqrt{3}}\]
done
clear
D)
\[l=m=n=\pm \frac{1}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 118) If a, b, c are in AP, a, mb, c are in GP, then \[a,{{m}^{2}}b,c\]care in:
A)
HP
done
clear
B)
GP
done
clear
C)
AP
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 119) If \[p\Rightarrow (q\vee r)\]is false, then the truth values of p, q, r are respectively:
A)
\[T,F,F\]
done
clear
B)
\[F,F,F\]
done
clear
C)
\[~F,T,T\]
done
clear
D)
\[T,T,F\]
done
clear
View Answer play_arrow
question_answer 120) In the expansion of \[{{(3x+2)}^{4}}\] the coefficient of middle term is:
A)
36
done
clear
B)
216
done
clear
C)
54
done
clear
D)
81
done
clear
View Answer play_arrow
question_answer 121) For any \[2\times 2\]matrix A, if \[A(adj\,A)=\left[ \begin{matrix} 10 & 0 \\ 0 & 10 \\ \end{matrix} \right],\] then | A | i.e., det A is equal to:
A)
20
done
clear
B)
100
done
clear
C)
10
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 122) The vectors \[\vec{a}=3\hat{i}-\hat{k},\vec{b}=\hat{i}+2\hat{j}\]are adjacent sides of a parallelogram. Its area is:
A)
\[\frac{1}{2}\sqrt{7}\]
done
clear
B)
\[\sqrt{41}\]
done
clear
C)
\[\frac{1}{2}\sqrt{41}\]
done
clear
D)
\[\frac{1}{2}\sqrt{17}\]
done
clear
View Answer play_arrow
question_answer 123) If a, b, care elements of a boolean algebra, then \[a.b+c(a+b)\]is equal to:
A)
\[a.b\]
done
clear
B)
c
done
clear
C)
\[a\,.\,b+c\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 124) \[(\vec{a}+\vec{b}).(\vec{a}-\vec{b})=0\]implies that:
A)
\[\vec{a}=-\vec{b}\]
done
clear
B)
\[\vec{a}\ne \vec{b}\]
done
clear
C)
\[|\vec{a}|=|\vec{b}|\]
done
clear
D)
\[\vec{a}=\vec{b}\]
done
clear
View Answer play_arrow
question_answer 125) 3 persons have 4 coats, 5 waist coats and 6 hats. The number of ways in which they put on the clothes are:
A)
\[{{4}^{3}}\times {{5}^{3}}\times {{6}^{3}}\]
done
clear
B)
\[4\times 5\times 6\]
done
clear
C)
\[4!5!6!\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 126) If an integer p is chosen at random in the interval \[0\le p\le 5,\]the probability that the roots of the equation \[{{x}^{2}}+px+\frac{p}{4}+\frac{1}{2}=0\] are real, is:
A)
\[\frac{4}{5}\]
done
clear
B)
\[\frac{2}{3}\]
done
clear
C)
\[\frac{3}{5}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 127) \[\int_{0}^{1}{x{{(1-x)}^{4}}dx}\]is equal to:
A)
1
done
clear
B)
0
done
clear
C)
\[\frac{1}{30}\]
done
clear
D)
\[\frac{1}{5}\]
done
clear
View Answer play_arrow
question_answer 128) The function\[f(x)=2-3x\]is:
A)
increasing
done
clear
B)
decreasing
done
clear
C)
neither decreasing nor increasing
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 129) The value of \[\int_{0}^{\pi /2}{\frac{\frac{\pi }{4}-x}{\sqrt{\sin x+\cos x}}dx}\]is:
A)
\[\frac{\pi \sqrt{3}}{4}\]
done
clear
B)
\[\frac{\pi }{4\sqrt{2}}\]
done
clear
C)
0
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 130) If \[y=\sqrt{x+\sqrt{x+\sqrt{x+....\infty ,}}}\]then \[\frac{dy}{dx}\]is equal to:
A)
\[\frac{1}{2y+1}\]
done
clear
B)
\[\frac{1}{2y-1}\]
done
clear
C)
\[\frac{1}{xy}\]
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 131) If \[f:A\to B\]is a bijection, then:
A)
\[n(A)=n(B)\]
done
clear
B)
\[n(A)\le n(B)\]
done
clear
C)
\[n(A)\ge n(s)\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 132) The equation of a straight line passing through \[(-3,2)\] and cutting an intercept equal in magnitude but opposite in sign from axis, is given by:
A)
\[x-y+5=0\]
done
clear
B)
\[x+y-5=0\]
done
clear
C)
\[~x-y-5=0\]
done
clear
D)
\[~x+y+5=0\]
done
clear
View Answer play_arrow
question_answer 133) If \[\frac{2{{z}_{1}}}{3{{z}_{2}}}\]is a purely imaginary number, then \[\left| \frac{{{z}_{1}}-{{z}_{2}}}{{{z}_{1}}+{{z}_{2}}} \right|\]is equal to:
A)
\[\frac{3}{2}\]
done
clear
B)
1
done
clear
C)
\[\frac{2}{3}\]
done
clear
D)
\[\frac{4}{9}\]
done
clear
View Answer play_arrow
question_answer 134) If \[pth,\text{ }qth,\text{ }rth,\text{ }sth\]terms of an arithmetic progression axe in geometric progression, then \[p-q,\,q-r\] and \[r-s\]are in:
A)
HP
done
clear
B)
GP
done
clear
C)
AP
done
clear
D)
no particular order
done
clear
View Answer play_arrow
question_answer 135) Two bodies are projected from the same point with the same velocity but in different directions. If the range in each case be R and times of flight be \[{{t}_{1}}\]and \[{{t}_{2}},\]then R is equal to:
A)
\[\frac{1}{2}g\,{{t}_{1}}{{t}_{2}}\]
done
clear
B)
\[g\,{{t}_{1}}{{t}_{2}}\]
done
clear
C)
\[\frac{1}{4}g\,{{t}_{1}}{{t}_{2}}\]
done
clear
D)
\[2g\,{{t}_{1}}{{t}_{2}}\]
done
clear
View Answer play_arrow
question_answer 136) The reciprocal of the eccentricity of rectangular hyperbola is:
A)
\[\frac{1}{\sqrt{2}}\]
done
clear
B)
\[\sqrt{2}\]
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 137) If \[y=\frac{{{a}^{{{\cos }^{-1}}x}}}{1+{{a}^{{{\cos }^{-1}}x}}},z={{a}^{{{\cos }^{-1}}x}},\]then \[\frac{dy}{dx}\]is equal to:
A)
\[\frac{1}{1+{{a}^{{{\cos }^{-1}}x}}}\]
done
clear
B)
\[\frac{1}{{{(1+{{a}^{{{\cos }^{-1}}x}})}^{2}}}\]
done
clear
C)
\[\frac{-1}{1+{{a}^{{{\cos }^{-1}}x}}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 138) The value of \[\sin {{600}^{o}}\,\cos {{330}^{o}}+\cos {{120}^{o}}\sin {{150}^{o}}\]is:
A)
1
done
clear
B)
\[-1\]
done
clear
C)
\[\frac{\sqrt{3}}{2}\]
done
clear
D)
\[\frac{1}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 139) The area of circle whose centre is \[(h,k)\] and radius a is:
A)
\[\pi {{a}^{2}}hk\,\text{sq}\,\text{unit}\]
done
clear
B)
\[\pi {{a}^{2}}\,\text{sq}\,\text{unit}\]
done
clear
C)
\[\pi ({{h}^{2}}+{{k}^{2}}-{{a}^{2}})\text{sq}\,\text{unit}\]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 140) If \[\left[ \begin{matrix} 3 & 1 \\ 4 & 1 \\ \end{matrix} \right]X=\left[ \begin{matrix} 5 & -1 \\ 2 & 3 \\ \end{matrix} \right]\], then X is equal to:
A)
\[\left[ \begin{matrix} -3 & 4 \\ -4 & 13 \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} 3 & 4 \\ 14 & 13 \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} -3 & 4 \\ 14 & -13 \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} 3 & -4 \\ -14 & 13 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 141) If\[\vec{a},\vec{b},\vec{c}\] are coplanar vectors, then \[[\vec{a}+\vec{b}\vec{b}+\vec{c}\vec{c}+\vec{a}]\] is equal to:
A)
\[2|\vec{a}\vec{b}\vec{c}|\]
done
clear
B)
\[|\vec{a}\vec{b}\vec{c}|\]
done
clear
C)
\[3|\vec{a}\vec{b}\vec{c}|\]
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 142) If the resultant of two unlike parallel forces of magnitudes 10 N and 16 N act along a line at a distance of 24 cm from the line of action of the smaller force is 8 N, then the distance between the lines of action of the force is:
A)
12 cm
done
clear
B)
8 cm
done
clear
C)
10.66 cm
done
clear
D)
18 cm
done
clear
View Answer play_arrow
question_answer 143) The resultant of two forces \[\vec{P}\]and \[\vec{Q}\]is of magnitude P. If the force \[\vec{P}\] is doubled, \[\vec{Q}\]remaining unaltered, then the new resultant will be:
A)
along \[\vec{P}\]
done
clear
B)
along \[\vec{Q}\]
done
clear
C)
at \[{{60}^{o}}\]to\[\vec{Q}\]
done
clear
D)
at right angle to \[\vec{Q}\]
done
clear
View Answer play_arrow
question_answer 144) If the ratio of the sum of m and \[n\]terms of an AP is \[{{m}^{2}}:{{n}^{2}},\]then the ratio of its \[mth\]and \[nth\]terms is:
A)
\[m-1:n-1\]
done
clear
B)
\[2m+1:2n+1\]
done
clear
C)
\[2m-1:2n-1\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 145) A body. dropped from a height \[h\]at time \[t=0\]reaches the ground at tune \[{{t}_{0}}.\]would have reached a height \[h/2\]at time:
A)
\[\frac{{{t}_{0}}}{2}\]
done
clear
B)
\[\frac{{{t}_{0}}}{\sqrt{2}}\]
done
clear
C)
\[t_{0}^{2}\]
done
clear
D)
\[\frac{1}{t_{0}^{2}}\]
done
clear
View Answer play_arrow
question_answer 146) The area in the first quadrant between \[{{x}^{2}}+{{y}^{2}}={{\pi }^{2}}\]and \[y=\sin x\]is:
A)
\[\frac{{{\pi }^{3}}}{4}sq\]unit
done
clear
B)
\[\frac{{{\pi }^{3}}-16}{4}\text{sq}\,\text{unit}\]
done
clear
C)
\[\frac{{{\pi }^{3}}-8}{2}\text{sq}\,\text{unit}\]
done
clear
D)
\[\frac{{{\pi }^{3}}-8}{4}sq\,unit\]
done
clear
View Answer play_arrow
question_answer 147) In triangle ABC, if\[~3a=b+c,\] then \[\cot \frac{B}{2}\cot \frac{C}{2}\] is equal to:
A)
\[\sqrt{3}\]
done
clear
B)
1
done
clear
C)
2
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 148) If \[f(x)=2x+{{\cot }^{-1}}x+\log (\sqrt{1+{{x}^{2}}}-x),\]then \[f(x)\]:
A)
increases in \[(-\infty ,\infty )\]
done
clear
B)
decreases in \[(0,\infty )\]
done
clear
C)
neither increases nor decreases in \[(0,\infty )\]
done
clear
D)
sometimes increases and sometimes decreases
done
clear
View Answer play_arrow
question_answer 149) The series \[(1+3){{\log }_{e}}3+\frac{1+{{3}^{2}}}{2!}{{({{\log }_{e}}3)}^{2}}\]\[+\frac{1+{{3}^{2}}}{3!}{{({{\log }_{e}}3)}^{2}}+...\]is equal to:
A)
28
done
clear
B)
30
done
clear
C)
25
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 150) \[\int_{{}}^{{}}{\frac{\cos 4x-1}{\cot x-\tan x}}dx\]is equal to:
A)
\[-\frac{1}{2}\cos 4x+c\]
done
clear
B)
\[-\frac{1}{4}\cos 4x+c\]
done
clear
C)
\[-\frac{1}{2}\sin 2x+c\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
 \[mgh=\frac{1}{2}k\,{{x}^{2}}\]
\[mgh=\frac{1}{2}k\,{{x}^{2}}\] 
 10 J
10 J 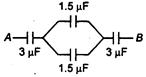 \[1\mu F\]
\[1\mu F\] 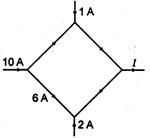 3 A
3 A