Solved papers for J & K CET Engineering J and K - CET Engineering Solved Paper-2013

done J and K - CET Engineering Solved Paper-2013 Total Questions - 225

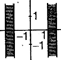
• question_answer1) Which of the following physical quantity unit is not a fundamental unit?
  A)
   Length            
  done clear
  B)
   Mass
  done clear
  C)
   Magnetic field      
  done clear
  D)
   Current
  done clear
  View Answer play_arrow

• question_answer2) The dimensional formula of electric potential is
  A)
   \[M{{L}^{2}}{{T}^{-3}}{{A}^{-1}}\]       
  done clear
  B)
   \[{{M}^{-1}}{{L}^{2}}{{T}^{-2}}A\]
  done clear
  C)
   \[{{M}^{-1}}{{L}^{2}}{{T}^{-2}}{{A}^{-1}}\]      
  done clear
  D)
   \[M{{L}^{2}}{{L}^{2}}{{T}^{-2}}A\]
  done clear
  View Answer play_arrow

• question_answer3) The motion of a particle in straight line is an example of
  A)
   constant velocity motion
  done clear
  B)
   uniformly accelerated motion
  done clear
  C)
   non-uniformly accelerated motion
  done clear
  D)
   zero velocity motion
  done clear
  View Answer play_arrow

• question_answer4) The velocity vector of the motion described by the position vector of a particle, \[r=2t\,\,\hat{i}+{{t}^{2}}\hat{j}\]is given by
  A)
   \[V=2i+2t\,\hat{j}\]      
  done clear
  B)
   \[V=2t\,\,\hat{i}+2t\,\hat{j}\]
  done clear
  C)
   \[V=t\,\,\hat{i}+{{t}^{2}}\,\hat{j}\]     
  done clear
  D)
   \[V=2\,\,\hat{i}+{{t}^{2}}\,\hat{j}\]
  done clear
  View Answer play_arrow

• question_answer5) The velocity-time graph of particle comes out to be a non-linear curve. The motion is
  A)
   uniform velocity motion
  done clear
  B)
   uniformly accelerated motion
  done clear
  C)
   non-uniform accelerated motion
  done clear
  D)
   nothing can be said about the motion
  done clear
  View Answer play_arrow

• question_answer6) A projectile is thrown with initial velocity \[{{\upsilon }_{0}}\] and angle \[{{30}^{o}}\] with the horizontal. If it remains in the air for \[1\text{ }s,\] what was its initial velocity?
  A)
   \[19.6\text{ }m/s\]           
  done clear
  B)
   \[9.8\text{ }m/s\]
  done clear
  C)
   \[4.9\text{ }m/s\]            
  done clear
  D)
   \[1\text{ }m/s\]
  done clear
  View Answer play_arrow

• question_answer7) Newton's second law of motion is
  A)
   \[F=dp/dt\]
  done clear
  B)
   \[F=mv\]
  done clear
  C)
   \[~F=m{{v}^{2}}\]          
  done clear
  D)
   \[~F={{m}^{2}}v\]
  done clear
  View Answer play_arrow

• question_answer8) The centripetal force is given by the expression
  A)
   \[\frac{M{{V}^{2}}}{R}\]                 
  done clear
  B)
   \[\frac{{{M}^{2}}V}{R}\]
  done clear
  C)
   \[\frac{Mv}{{{R}^{2}}}\]
  done clear
  D)
    \[\frac{Mv}{R}\]
  done clear
  View Answer play_arrow

• question_answer9) Uniform circular motion is an example of
  A)
   constant speed motion
  done clear
  B)
   constant velocity motion
  done clear
  C)
   non-accelerated motion
  done clear
  D)
   zero accelerated motion
  done clear
  View Answer play_arrow

• question_answer10) The  scalar product of two vectors \[A=2\hat{i}+2\hat{j}-\hat{k}\] and \[B=-\hat{j}+\hat{k},\] is given by
  A)
   \[A.B=3\]          
  done clear
  B)
   \[A.B=4\]
  done clear
  C)
   \[A.B=-4\]        
  done clear
  D)
   \[A.B=-3\]
  done clear
  View Answer play_arrow

• question_answer11) The linear momentum is conserved in
  A)
   elastic collisions    
  done clear
  B)
   inelastic collisions
  done clear
  C)
   Both 1 and 2       
  done clear
  D)
   Neither 1 nor 2
  done clear
  View Answer play_arrow

• question_answer12) The power (P) of an engine lifting a mass of \[100\text{ }kg\]up to a height of \[10\text{ }m\]in \[1\text{ }min\]is
  A)
   \[P=163.3\,\,W\]
  done clear
  B)
   \[P=9800\text{ }W\]
  done clear
  C)
   \[P=10000\text{ }W\]
  done clear
  D)
   \[P=5000\,\,W\]
  done clear
  View Answer play_arrow

• question_answer13) The conservation of angular momentum  demands that
  A)
   the external force on the system must be zero
  done clear
  B)
   the external torque on the system must be zero
  done clear
  C)
   both the external force as well as the external torque must be zero           
  done clear
  D)
   neither of them must be zero
  done clear
  View Answer play_arrow

• question_answer14) The moment of inertia (J) and the angular momentum (L) are related by the expression
  A)
   \[I=L\omega \]            
  done clear
  B)
   \[L=I\omega \]
  done clear
  C)
    \[L={{I}^{2}}\omega \]          
  done clear
  D)
   \[\omega =LI\] where (0 is the angular velocity.
  done clear
  View Answer play_arrow

• question_answer15) The moment of inertia (J) of a sphere of radius R and mass M is given by
  A)
   \[I=M{{R}^{2}}\]
  done clear
  B)
   \[I=(1/2)M{{R}^{2}}\]
  done clear
  C)
   \[I=(4/3)M{{R}^{2}}\]     
  done clear
  D)
   \[I=(2/5)M{{R}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer16) The universal law of gravitation is the force law known also as the
  A)
   triangular law       
  done clear
  B)
   square law
  done clear
  C)
   inverse square law  
  done clear
  D)
   parallelogram law
  done clear
  View Answer play_arrow

• question_answer17) The value of acceleration due to gravity at the surface of earth
  A)
   is maximum at the poles
  done clear
  B)
   is maximum at the equator
  done clear
  C)
   remains constant everywhere on the surface of the earth
  done clear
  D)
   is maximum at the international timeline
  done clear
  View Answer play_arrow

• question_answer18) The escape velocity of a particle from the surface of the earth is given by
  A)
   \[{{(g/R)}^{1/2}}\]
  done clear
  B)
   \[{{(2\,gR)}^{1/2}}\]          
  done clear
  C)
   \[{{(3\,\,gR)}^{1/2}}\]
  done clear
  D)
   \[{{(\,gR/2)}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer19) The Young's modulus of a rope of \[10\text{ }m\] length and having diameter of \[2\text{ }cm\]is \[200\times {{10}^{11}}\,dyne/c{{m}^{2}}\]. If the elongation produced in the rope is \[1\text{ }cm,\] the force applied on the rope is
  A)
   \[6.28\times {{10}^{5}}\,\,N\]
  done clear
  B)
   \[6.28\times {{10}^{4}}\,\,N\]
  done clear
  C)
   \[6.28\times {{10}^{4}}\text{ }dyne\]   
  done clear
  D)
   \[6.28\times {{10}^{5}}\text{ }dyne\]
  done clear
  View Answer play_arrow

• question_answer20) "The pressure exerted at any point in an enclosed fluid is transmitted equally in all directions". This is known as
  A)
   Archimedes 'principle
  done clear
  B)
   Law of floatation
  done clear
  C)
   Pascal?s law
  done clear
  D)
   Bernoulli principal
  done clear
  View Answer play_arrow

• question_answer21) There    are   two identical small holes on the opposite sides of a tank containing a liquid. The tank is open at the top. The difference in height between the two holes is h. As the liquid comes out of the two holes, the tank will experience   a   net   horizontal   force proportional to
  A)
   \[\sqrt{h}\]              
  done clear
  B)
   \[h\]
  done clear
  C)
   \[{{h}^{3/2}}\]             
  done clear
  D)
   \[{{h}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer22) The zeroth law of thermodynamics for three systems A, B and C in contact demands that
  A)
   A and B are in thermal equilibrium
  done clear
  B)
   B and C are in thermal equilibrium
  done clear
  C)
   A and C are in thermal equilibrium
  done clear
  D)
   A B and C are in thermal equilibrium
  done clear
  View Answer play_arrow

• question_answer23) The efficiency of a Carnot engine kept at the temperatures of \[{{27}^{o}}C\] and \[{{127}^{o}}C\] is
  A)
   \[20%\]  
  done clear
  B)
   \[25%\]  
  done clear
  C)
   \[30%\]   
  done clear
  D)
   \[40%\]
  done clear
  View Answer play_arrow

• question_answer24) The average pressure of an ideal gas is
  A)
   \[p=(1/3)mnV_{av}^{2}\]
  done clear
  B)
   \[p=(1/3)mn{{V}_{av}}\]
  done clear
  C)
   \[p=(1/4)mnV_{av}^{2}\]
  done clear
  D)
   \[p=(1/3)mn{{V}_{av}}\] where symbols have their usual meanings.
  done clear
  View Answer play_arrow

• question_answer25) According to equipartition law of energy each particle in a system of particles have thermal energy E equal to
  A)
   \[E={{k}_{B}}T\]
  done clear
  B)
   \[E=(1/2){{k}_{B}}T\]
  done clear
  C)
   \[E=3\,\,{{k}_{B}}T\]
  done clear
  D)
   \[E=(3/2)\,\,{{k}_{B}}T\]          
  done clear
  View Answer play_arrow

• question_answer26) The velocity of sound in a gas is \[1300\text{ }m/s\]at STP and specific heat at constant pressure is \[6.84\,cal\,{{K}^{-1}}\,mo{{l}^{-1}}\]. The rms velocity at STP is \[(R=1.98\,cal\,\,{{K}^{-1}}\,mo{{l}^{-1}})\]
  A)
   \[1300\text{ }m/s\]
  done clear
  B)
   \[2600\text{ }m/s\]
  done clear
  C)
   \[1898\text{ }m/s\]
  done clear
  D)
   \[650\text{ }m/s\]
  done clear
  View Answer play_arrow

• question_answer27) The time period of a simple pendulum of length \[9.8\text{ }m\]is
  A)
   \[0.159\,\,s\]
  done clear
  B)
   \[3.14\,\,s\]
  done clear
  C)
   \[6.5\,\,s\]
  done clear
  D)
   \[6.28\text{ }s\]
  done clear
  View Answer play_arrow

• question_answer28) The displacement, velocity and acceleration in   a simple harmonic motion are related as the
  A)
   displacement, velocity and acceleration all act in the same direction
  done clear
  B)
   displacement and velocity act in the same direction but acceleration in the opposite direction
  done clear
  C)
   Velocity and acceleration are parallel and both are perpendicular to the displacement
  done clear
  D)
   displacement and acceleration are antiparallel and both perpendicular to the velocity
  done clear
  View Answer play_arrow

• question_answer29) The beats are the examples of
  A)
   simple harmonic motion
  done clear
  B)
   interference of two or more waves having same amplitude but slightly different frequencies in the same direction          
  done clear
  C)
   interference of two or more waves having different amplitude but same frequencies in the same direction
  done clear
  D)
   interference of two or more waves having same amplitude out slightly different frequencies in the perpendicular direction
  done clear
  View Answer play_arrow

• question_answer30) The fundamental frequency of an open pipe of length \[1\text{ }m,\] if the speed of sound in air is \[340\text{ }m/s\]is
  A)
   \[340\text{ }Hz\]          
  done clear
  B)
   \[170\text{ }Hz\]
  done clear
  C)
   \[680\text{ }Hz\]          
  done clear
  D)
   \[85\text{ }Hz\]
  done clear
  View Answer play_arrow

• question_answer31) A whistle with frequency \[1020\text{ }Hz\]is blown at a station. A man travelling in train moving towards the station at \[30\text{ }m/s\]hears the sound of the whistle. If the speed of sound is \[340\text{ }m/s,\] the apparent frequency heard by him is
  A)
   \[1020\text{ }Hz\]          
  done clear
  B)
   \[1110\text{ }Hz\]
  done clear
  C)
   \[2040\text{ }Hz\]          
  done clear
  D)
   \[610\text{ }Hz\]
  done clear
  View Answer play_arrow

• question_answer32) An electric charge does not have which of hte following properties?
  A)
   Total charge conservation
  done clear
  B)
   Quantization of charge
  done clear
  C)
   Two type of charge
  done clear
  D)
   Circular line of force
  done clear
  View Answer play_arrow

• question_answer33) The net electric force on a charge of \[+3\mu C\] at the mid-point on the line joining two charges of magnitude \[+2\mu C\] and \[-2\mu C\] separated by the distance of \[6mm,\]is
  A)
   \[6000\,N\]
  done clear
  B)
   \[500\,N\]
  done clear
  C)
   \[60\,N\]
  done clear
  D)
   zero
  done clear
  View Answer play_arrow

• question_answer34) A hollow sphere of radius \[0.1\text{ }m\] has a charge of \[5\times {{10}^{-8}}C.\]. The potential at a distance of \[5\text{ }cm\]from the centre of the  sphere is \[=\left( \frac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}\,\,N{{m}^{2}}\,\,{{C}^{-2}} \right)\]
  A)
   \[4000\,V\]
  done clear
  B)
   \[4500\,V\]
  done clear
  C)
   \[5000\,V\]
  done clear
  D)
   \[6000\,V\]
  done clear
  View Answer play_arrow

• question_answer35) A parallel plate capacitor of capacitance 5 microfarad is charged to \[120\text{ }V\]and then connected to another uncharged  capacitor. If the potential falls to \[40\text{ }V,\] and capacitance of the second capacitor is
  A)
   5 microfarad      
  done clear
  B)
   10 microfarad
  done clear
  C)
   15 microfarad     
  done clear
  D)
   20 microfarad
  done clear
  View Answer play_arrow

• question_answer36) Two identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is
  A)
   \[1:1\]    
  done clear
  B)
   \[1:2\]
  done clear
  C)
   \[1:3\]   
  done clear
  D)
   \[1:4\]
  done clear
  View Answer play_arrow

• question_answer37) An electron revolves in a circle at the rate of 1019 rounds per second. The equivalent current is \[(e=1.6\times {{10}^{-19}}C)\]
  A)
   \[1.0\,\,A\]            
  done clear
  B)
   \[1.6\,\,A\]
  done clear
  C)
   \[2.0\text{ }A\]            
  done clear
  D)
   \[2.6\text{ }A~\]
  done clear
  View Answer play_arrow

• question_answer38) A silver wire of radius \[0.1\text{ }cm\]carries a current of\[2A\]. If the charge density in silver is \[5.86\times {{10}^{28}}{{m}^{-3}},\] the drift velocity is
  A)
   \[0.2\times {{10}^{-3}}m/s\]
  done clear
  B)
   \[0.4\times {{10}^{-4}}\text{ }m/s\]
  done clear
  C)
   \[0.68\times {{10}^{-4}}\text{ }m/s\]    
  done clear
  D)
  \[7\times {{10}^{-4}}\text{ }m/s\]                    
  done clear
  View Answer play_arrow

• question_answer39) A \[1\,m\] long wire of diameter of  \[0.31\text{ }mm\] has a resistance of \[4.2\Omega \]. If it is replaced by another wire of same material of length \[1.5\text{ }m\]and diameter \[0.155\text{ }mm,\] the resistance of wire is
  A)
   \[25.2\text{ }\Omega \]             
  done clear
  B)
   \[0.6\text{ }\Omega \]
  done clear
  C)
    \[26.7\text{ }\Omega \]              
  done clear
  D)
   \[\text{0}\text{.8 }\Omega \]
  done clear
  View Answer play_arrow

• question_answer40) 24 cells of emf \[1.5\text{ }V\]each having internal resistance of \[1\text{ }ohm\]are connected to an  external resistance of\[1.5\text{ }ohms\]. To get maximum current
  A)
   all cells are connected in series combination
  done clear
  B)
   all cells are connected in parallel combination
  done clear
  C)
   4 cells in each row are connected in series and6 such rows are connected in parallel
  done clear
  D)
   6 cells in each row are connected in series and 4 such rows are connected in parallel
  done clear
  View Answer play_arrow

• question_answer41) The temperature coefficient of the resistance of a wire is\[0.00125\text{ }per{{\text{ }}^{o}}C\]. At \[300\text{ K}\]its resistance is \[1\Omega \]. The resistance of wire will be \[2\,\,\Omega ,\] at
  A)
   \[1154\,\,K\]            
  done clear
  B)
   \[1100\,\,K\]
  done clear
  C)
   \[1400\text{ }K\]            
  done clear
  D)
   \[1127\,\,K\]
  done clear
  View Answer play_arrow

• question_answer42) A long straight wire is carrying a current of\[12\text{ }A\]334. The magnetic field at a distance of \[8\text{ }cm\]is \[({{\mu }_{0}}=4\pi \times {{10}^{-7}}\,\,N/{{A}^{2}})\]
  A)
  \[2\times {{10}^{-4}}Wb/{{m}^{2}}\]   
  done clear
  B)
   \[3\times {{10}^{-5}}\text{ }Wb/{{m}^{2}}\]
  done clear
  C)
   \[4\times {{10}^{-4}}Wb/{{m}^{2}}\]   
  done clear
  D)
   \[4\times {{10}^{-5}}\text{ }Wb/{{m}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer43) The magnetic field at a point on the axis of a long solenoid having 5 turns per cm length when a current of \[0.8\,A\]flows through it is
  A)
   \[5.024\times {{10}^{-8}}\text{ }Wb/{{m}^{2}}\]
  done clear
  B)
   \[6.024\times {{10}^{-8}}\text{ }Wb/{{m}^{2}}\]
  done clear
  C)
   \[7.024\times {{10}^{-8}}\text{ }Wb/{{m}^{2}}\]
  done clear
  D)
   \[8.024\times {{10}^{-8}}\text{ }Wb/{{m}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer44) Two straight wires each \[10\text{ }cm\]long are parallel to one another and separated by\[2\text{ }cm\]. When the current flowing in them is \[30\text{ }A\]and \[40\text{ }A\]respectively, the force experienced by either of the wires is
  A)
   \[1.2\times {{10}^{-3}}N\]        
  done clear
  B)
   \[12\times {{10}^{-3}}N\]
  done clear
  C)
   \[11.2\times {{10}^{-3}}\text{ }N\]     
  done clear
  D)
   \[10.2\times {{10}^{-3}}\text{ }N\]
  done clear
  View Answer play_arrow

• question_answer45) The horizontal and vertical components of earth's magnetic field at a place are \[0.3\text{ }G\] and\[0.52\text{ }G\]. The earth's magnetic field and the angle of dip are
  A)
   \[0.3\text{ }G\]and \[\delta ={{30}^{o}}\]
  done clear
  B)
   \[0.4\text{ }G\]and \[\delta ={{40}^{o}}\]
  done clear
  C)
   \[0.5\text{ }G\]and \[\delta ={{50}^{o}}\]   
  done clear
  D)
   \[0.6\text{ }G\]and \[\delta ={{60}^{o}}\]
  done clear
  View Answer play_arrow

• question_answer46) A bar magnet of pole strength \[10\text{ }Am\]is cut into two equal parts breadthwise. The pole strength of each magnet is
  A)
   \[5\text{ }Am\]
  done clear
  B)
  \[~10\text{ }Am\]
  done clear
  C)
   \[15\text{ }Am\]          
  done clear
  D)
   \[20\text{ }Am\]
  done clear
  View Answer play_arrow

• question_answer47) A conductor of length \[5\text{ }cm\]is moved  parallel to itself with a speed of \[2\text{ }m/s,\] perpendicular to a uniform magnetic field of\[{{10}^{-3}}\text{ }Wb/{{m}^{3}}\]. The induced e.m.f. generated is
  A)
   \[2\times {{10}^{-3}}V\]        
  done clear
  B)
   \[1\times {{10}^{-3}}V\]
  done clear
  C)
   \[1\times {{10}^{-4}}V\]        
  done clear
  D)
   \[2\times {{10}^{-4}}V\]
  done clear
  View Answer play_arrow

• question_answer48) The induced emf in a coil of \[10\text{ }H\]inductance in which current varies from \[9\text{ }A\]to \[4\text{ }A\]in \[0.2\,\,s\] is
  A)
   \[200\,\,V\]             
  done clear
  B)
   \[250\,\,V\]
  done clear
  C)
   \[300\,\,V\]             
  done clear
  D)
   \[350\,\,V\]
  done clear
  View Answer play_arrow

• question_answer49) The alternating current in a circuit is given by \[I=50\,\,\sin \,\,314t\]. The peak value and frequency of the current are
  A)
   \[{{I}_{0}}=25\,\,A\]and \[f=100\,\,Hz\]
  done clear
  B)
   \[{{I}_{0}}=50\,\,Hz\]  and \[f=50\,Hz\]
  done clear
  C)
   \[{{I}_{0}}=50A\] and \[f=100\,\,Hz\]
  done clear
  D)
   \[{{\text{I}}_{0}}=25A\]and  \[f=50\,\,Hz\]
  done clear
  View Answer play_arrow

• question_answer50) A 5\[50\text{ }Hz\] AC signal is applied in a circuit of inductance of \[(1/\pi )H\] and resistance \[2100\,\Omega \]The impedance offered by the circuit is
  A)
   \[1500\text{ }\Omega \]           
  done clear
  B)
   \[1700\,\,\Omega \]
  done clear
  C)
   \[2102\,\Omega \]           
  done clear
  D)
   \[2500\,\,\Omega \]
  done clear
  View Answer play_arrow

• question_answer51) If     the     alternating     current \[I={{I}_{1}}\,\,\cos \,\,\,\omega t+{{I}_{2}}\,\,\sin \,\,\omega t\](of  then  the  rms current is given by
  A)
   \[\frac{{{I}_{1}}+{{I}_{2}}}{\sqrt{2}}\]
  done clear
  B)
   \[\frac{|{{I}_{1}}+{{I}_{2}}|}{\sqrt{2}}\]
  done clear
  C)
   \[\sqrt{\left( \frac{I_{1}^{2}+I_{2}^{2}}{2} \right)}\]
  done clear
  D)
   \[\sqrt{\frac{I_{1}^{2}+I_{2}^{2}}{\sqrt{2}}}\]
  done clear
  View Answer play_arrow

• question_answer52) The transverse nature of electromagnetic waves is proved by which of the following?
  A)
   Interference phenomena
  done clear
  B)
   Diffraction phenomena
  done clear
  C)
   Dispersion phenomena
  done clear
  D)
   Polarization phenomena
  done clear
  View Answer play_arrow

• question_answer53) Which component of electromagnetic spectrum have maximum wavelength?
  A)
   Radio waves
  done clear
  B)
   Visible spectrum
  done clear
  C)
   Gamma rays
  done clear
  D)
   X-rays
  done clear
  View Answer play_arrow

• question_answer54) An object is 8 cm high. It is desired to form a real image \[4\text{ }cm\]high at \[60\text{ }cm\]from the mirror. The type of mirror needed with the focal length is
  A)
   convex mirror with focal length \[f=40\text{ }cm\]
  done clear
  B)
   convex mirror with focal length \[f=20\text{ }cm\]
  done clear
  C)
   concave mirror with focal length \[f=-40\text{ }cm\]
  done clear
  D)
   concave mirror with focal length \[f=-20\text{ }cm\]
  done clear
  View Answer play_arrow

• question_answer55) When an object is placed \[40\text{ }cm\]from a diverging lens, its virtual image is formed \[20\text{ }cm\]from the lens. The focal length and power of lens are
  A)
   \[F=-20cm,\,P=-5\,D\]
  done clear
  B)
   \[F=-40cm,\,P=-5\,D\]
  done clear
  C)
   \[F=-40cm,\,P=-2.5\,D\]
  done clear
  D)
   \[F=-20\,cm,\,P=-2.5\,D\]
  done clear
  View Answer play_arrow

• question_answer56) A magnifying glass of focal length \[5\text{ }cm\]is used to view an object by a person whose smallest distance of distinct vision is\[25\text{ }cm\]. If he holds the glass close to eye, the magnification is
  A)
   \[5\]      
  done clear
  B)
   \[6\]
  done clear
  C)
   \[2.5\]   
  done clear
  D)
   \[3\]
  done clear
  View Answer play_arrow

• question_answer57) A person has a minimum distance of distinct vision as\[50\text{ }cm\]. The power of lenses required to read a book at a distance of \[25\text{ }cm\]is
  A)
   \[3\,\,D\]                  
  done clear
  B)
   \[1\,\,D\]
  done clear
  C)
   \[2\,\,D\]                   
  done clear
  D)
   \[4\,\,D\]
  done clear
  View Answer play_arrow

• question_answer58) If two slits in Young's experiment are \[0.4\text{ }mm\]apart and fringe width on a screen \[200\text{ }cm\]away is \[2\text{ }mm\]the wavelength of light illuminating the slits is
  A)
   \[500\text{ }nm\]          
  done clear
  B)
   \[600\text{ }nm\]
  done clear
  C)
   \[400\text{ }nm\]         
  done clear
  D)
   \[300\text{ }nm\]
  done clear
  View Answer play_arrow

• question_answer59) Electric field strength due to a diple at a point on the axial line of dipole is
  A)
   from positive charge to negative charge
  done clear
  B)
   from negative charge to positive charge
  done clear
  C)
   along the equatorial line
  done clear
  D)
   at an angle to axial line
  done clear
  View Answer play_arrow

• question_answer60) The distance of moon form the earth is \[3.8\times {{10}^{5}}\text{ }km\]. Supposing that the eye is most sensitive to the light of wavelength \[550\text{ }nm,\] the separation of two points on the moon that can be resolved by a \[500\text{ }cm\]telescope is
  A)
   \[50\,\,m\]               
  done clear
  B)
   \[55\,\,m\]
  done clear
  C)
   \[51\text{ }m\]                
  done clear
  D)
   \[60\,\,m\]
  done clear
  View Answer play_arrow

• question_answer61) Unpolarized light falls on two polarizing sheets placed one on top of other. If the intensity of transmitted light is one fourth of the incident light, the angle between them is
  A)
   \[{{35}^{o}}\]   
  done clear
  B)
   \[{{40}^{o}}\]
  done clear
  C)
   \[{{45}^{o}}\]   
  done clear
  D)
   \[{{50}^{o}}\]
  done clear
  E)
  Not available
  done clear
  View Answer play_arrow

• question_answer62) The Brewster's law is given by the expression
  A)
   \[\mu =\frac{\sin \,i}{\sin \,r}\]
  done clear
  B)
   \[\mu =\tan \,{{\theta }^{o}}\]
  done clear
  C)
   \[\mu =\cos \theta \]
  done clear
  D)
   \[\mu =sin\theta \]
  done clear
  View Answer play_arrow

• question_answer63) Einstein's photoelectric equation is
  A)
   \[{{E}_{\max }}=hv-\phi \]
  done clear
  B)
   \[E=m{{c}^{2}}\]
  done clear
  C)
   \[{{E}^{2}}={{p}^{2}}{{c}^{2}}+m_{0}^{2}{{c}^{4}}\]
  done clear
  D)
   \[E=\left( \frac{1}{2} \right)m{{v}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer64) The Davission-Germer experiment is the direct evidence of
  A)
   particle nature of electrons
  done clear
  B)
   wave nature of electrons
  done clear
  C)
   wave nature of light
  done clear
  D)
   particle nature of light
  done clear
  View Answer play_arrow

• question_answer65) The Rutherford scattering experiment porves that an atom consists of
  A)
   a sphere of positive charge in which electrons are embedded like seeds of water-melon
  done clear
  B)
   a sphere of negative charge in which protons are embedded like seeds of water-melon
  done clear
  C)
   a sphere of electron cloud in which the positive charge in placed at the centre of the sphere
  done clear
  D)
   a sphere of neutral charge
  done clear
  View Answer play_arrow

• question_answer66) According to Bohr model of hydrogen atom, only those orbits are permissible which satisfy the condition
  A)
   \[mv=nh\]
  done clear
  B)
   \[\frac{m{{v}^{2}}}{r}=n\left( \frac{h}{2\pi } \right)\]
  done clear
  C)
   \[mvr=n\left( \frac{h}{2\pi } \right)\]
  done clear
  D)
   \[mv{{r}^{2}}=n\left( \frac{h}{2\pi } \right)\]
  done clear
  View Answer play_arrow

• question_answer67) The radioactive decay of thorium \[(A=232,\,\,Z=90)\] releases six alpha and four beta particles. The atomic number and mass number of the final product is                  
  A)
   \[Z=80,\,\,A=207\]                                
  done clear
  B)
   \[Z=82,\,\,A=208\]                   
  done clear
  C)
   \[Z=92,\,\,A=209\]                           
  done clear
  D)
   \[Z=90,\,\,A=207\]                                   
  done clear
  View Answer play_arrow

• question_answer68) Polonium has a half-life of \[140\] days. If we take \[20\,\,g\]of polonium initially then the amount of  it that remains after 280 days is       
  A)
   \[2.5\,\,g\]             
  done clear
  B)
   \[5\,\,g\]              
  done clear
  C)
   \[10\text{ }g\]             
  done clear
  D)
   \[15\text{ }g\]
  done clear
  View Answer play_arrow

• question_answer69) Based on the band theory of conductors, insulators  and  semi-conductors,  the forbidden gap is smallest in
  A)
   conductors         
  done clear
  B)
   insulators
  done clear
  C)
   semi-conductors    
  done clear
  D)
   All of these
  done clear
  View Answer play_arrow

• question_answer70) Based on the I-V characteristics of the diode, we can classify diode as
  A)
   bi-directional device
  done clear
  B)
   ohmic device
  done clear
  C)
   non-ohmic device   
  done clear
  D)
   passive element
  done clear
  View Answer play_arrow

• question_answer71) The Boolean expression for the XOR gate is
  A)
   \[Y=A+B\]         
  done clear
  B)
   \[Y=A.B\]
  done clear
  C)
   \[Y=AB=BA\]       
  done clear
  D)
   \[Y=A\oplus B\]
  done clear
  View Answer play_arrow

• question_answer72) Which of the following logic gates are also known as the Universal gates?
  A)
   AND, OR. NOT gate
  done clear
  B)
   XOR, XNOR gate
  done clear
  C)
   NAND, NOR gate
  done clear
  D)
   All logic gates
  done clear
  View Answer play_arrow

• question_answer73) The length of antenna (L) required to propagate a signal of wavelength \[\lambda \] is given as
  A)
   \[L=\frac{\lambda }{2}\]
  done clear
  B)
   \[L=2\lambda \]
  done clear
  C)
   \[L=\frac{\lambda }{3}\]
  done clear
  D)
   \[L=\frac{\lambda }{4}\]
  done clear
  View Answer play_arrow

• question_answer74) The modulation is the process in which the
  A)
   modulating signal is sent by antenna in the air
  done clear
  B)
   carrier signal is sent by the antenna in the air
  done clear
  C)
   modulated signal formed by the mixing of modulating signal with the carrier signal is sent by the antenna
  done clear
  D)
   modulated signal formed by the mixing of modulating signal with the carrier signal is received by a receiver antenna
  done clear
  View Answer play_arrow

• question_answer75) The demodulator or detector circuit consists of a
  A)
   resistor             
  done clear
  B)
   transistor
  done clear
  C)
   diode               
  done clear
  D)
   capacitor
  done clear
  View Answer play_arrow

• question_answer76) Which of the following would contain the same number of atoms as 20 g of calcium? [At. masses:\[Ca=40,Mg=24,C=12\]]
  A)
   24 g of magnesium
  done clear
  B)
   12 got carbon
  done clear
  C)
   24 got carbon
  done clear
  D)
   12 g of magnesium
  done clear
  View Answer play_arrow

• question_answer77) 100 mL of \[\text{N}{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\]is mixed with 100 mL of \[\text{1 M NaOH}\]solution. The resulting solution will be
  A)
   highly acidic         
  done clear
  B)
   neutral
  done clear
  C)
   highly basic         
  done clear
  D)
   slightly acidic
  done clear
  View Answer play_arrow

• question_answer78) The bond order of\[\text{N}_{\text{2}}^{\text{+}}\]on the basis of molecular orbital theory is [Atomic number of\[\text{N}\,\text{=}\,\text{7}\]]
  A)
   3       
  done clear
  B)
   2.5     
  done clear
  C)
   2       
  done clear
  D)
   1.5
  done clear
  View Answer play_arrow

• question_answer79) What is the total number of electrons that can  have the values \[n=2,l=1,s=1/2\]in the electronic configuration\[1{{s}^{2}}2{{s}^{2}}2{{p}^{3}}\]
  A)
   1       
  done clear
  B)
   3       
  done clear
  C)
   5       
  done clear
  D)
   7
  done clear
  View Answer play_arrow

• question_answer80) Calculate the wavelength associated with an electron moving with a velocity of \[{{10}^{6}}\,m/s\](mass   of   electron \[=9.1\times {{10}^{-31}}\,kg,\]\[h=6.6\times {{10}^{-34}}\,kg\,{{m}^{2}}\,{{s}^{-1}}\])
  A)
   \[6.2\times {{10}^{-8}}\,m\]
  done clear
  B)
  \[7.25\times {{10}^{-8}}\,m\]
  done clear
  C)
   \[6.25\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
  done clear
  D)
   None of the above
  done clear
  View Answer play_arrow

• question_answer81) Which of the following pairs is not correctly matched?
  A)
   Hund's rule In orbitals of equivalent energy electron spins remain unpaired if possible
  done clear
  B)
   Pauli's exclusion No two electrons can principle have all the four quantum numbers identical
  done clear
  C)
   Zeeman effect The effect of magnetic field on the atomatic spectra
  done clear
  D)
   Uncertainty It is impossible to principle determine the position of an electron
  done clear
  View Answer play_arrow

• question_answer82) The orbital diagram in which Aufbau principle is violated is
  A)
   
  done clear
  B)
   
  done clear
  C)
   
  done clear
  D)
   
  done clear
  View Answer play_arrow

• question_answer83) The \[{{[\text{OH}]}^{-}}\]in a solution is \[1\,\text{mol}\,{{\text{L}}^{-1}}.\] The pH of the solution is
  A)
   1      
  done clear
  B)
   0      
  done clear
  C)
   14     
  done clear
  D)
   \[{{10}^{-14}}\]
  done clear
  View Answer play_arrow

• question_answer84) The solubility of \[\text{Fe(OH}{{\text{)}}_{\text{3}}}\]is \[x\,\text{mol}\,{{\text{L}}^{-1}}.\]Its\[{{K}_{sp}}\] would be
  A)
   \[9{{x}^{3}}\]
  done clear
  B)
   \[3{{x}^{3}}\]
  done clear
  C)
   \[27{{x}^{4}}\]
  done clear
  D)
  \[9{{x}^{4}}\]
  done clear
  View Answer play_arrow

• question_answer85) In which of the following reactions, increase in pressure will favour the forward reaction?
  A)
  \[PC{{l}_{5}}(g)\rightleftharpoons PC{{l}_{3}}(g)+C{{l}_{2}}(g)\]
  done clear
  B)
   \[2NO(g)+{{O}_{2}}(g)\rightleftharpoons 2N{{O}_{2}}(g)\]
  done clear
  C)
   \[C(s)+{{H}_{2}}O(g)\rightleftharpoons CO(g)+{{H}_{2}}(g)\]
  done clear
  D)
   \[2HI(g)\rightleftharpoons {{H}_{2}}(g)+{{I}_{2}}(g)\]
  done clear
  View Answer play_arrow

• question_answer86) Which of the following is a Lewis acid?
  A)
  \[BF_{4}^{-}\]
  done clear
  B)
  \[O{{H}^{-}}\]
  done clear
  C)
   \[AlC{{l}_{3}}\]
  done clear
  D)
   \[RN{{H}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer87) According to collision theory of chemical reactions rates of the reaction increase with increase in the temperature of a reaction because of
  A)
   increase in the velocity of the reacting molecules
  done clear
  B)
   increase in the number of collisions
  done clear
  C)
   increase in the number of molecules having the activation energy (threshold energy)
  done clear
  D)
   None of the above        
  done clear
  View Answer play_arrow

• question_answer88) Consider the reaction, \[2{{N}_{2}}O{{}_{5}}(g)\xrightarrow{{}}4N{{O}_{2}}(g)+{{O}_{2}}(g)\] The rate law for this reaction is rate\[=k[{{N}_{2}}{{O}_{5}}].\] Which of the following statements is true regarding the above reaction?
  A)
   Its order is 1 and molecularity is 1
  done clear
  B)
   Its order is 1 and molecularity is 2
  done clear
  C)
   Its order is 2 and molecularity is 2
  done clear
  D)
   Its order is 2 and molecularity is 1
  done clear
  View Answer play_arrow

• question_answer89) A catalyst is a substance which
  A)
   increases the rate of forward reaction in reversible reaction
  done clear
  B)
   increases the rate of both forward and backward reaction in a reversible reaction
  done clear
  C)
   does not influence a reversible reaction
  done clear
  D)
   increases the rate of backward reaction in a reversible reaction.
  done clear
  View Answer play_arrow

• question_answer90) Which of the following solutions will have the highest boiling point?
  A)
   1 M glucose solution
  done clear
  B)
   1 M sodium nitrate solution
  done clear
  C)
   1 M barium chloride solution
  done clear
  D)
   1 M aluminium chloride solution
  done clear
  View Answer play_arrow

• question_answer91) Which of the following is a colligative property?
  A)
   Lowering of vapour pressure
  done clear
  B)
   Osmotic pressure
  done clear
  C)
   Boiling point
  done clear
  D)
   Change in entropy
  done clear
  View Answer play_arrow

• question_answer92) van't Hoff factor for \[\text{Ca(N}{{\text{O}}_{\text{3}}}{{\text{)}}_{\text{2}}}\]is
  A)
   1                     
  done clear
  B)
   2
  done clear
  C)
   3                     
  done clear
  D)
   4
  done clear
  View Answer play_arrow

• question_answer93) What will be the freezing point of 1% solution of glucose in water, given that molal depression constant for water is \[1.84\,\text{K}\,\text{mo}{{\text{l}}^{-}}\]
  A)
   272.898 K         
  done clear
  B)
  \[~0.102{{\,}^{o}}C\]
  done clear
  C)
   273 K             
  done clear
  D)
  \[108{{\,}^{o}}C\]
  done clear
  View Answer play_arrow

• question_answer94) If\[\Delta H\]and\[\Delta S\]are positive for a reaction, the reaction will be spontaneous only when
  A)
   \[T\Delta S=\Delta H\]
  done clear
  B)
  \[T\Delta S>\Delta H\]
  done clear
  C)
   \[T\Delta S<\Delta H\]
  done clear
  D)
  \[T\Delta S\]is negative
  done clear
  View Answer play_arrow

• question_answer95) Calculate the enthalpy change for the reaction, \[{{C}_{2}}{{H}_{4}}(g)+{{H}_{2}}(g)\xrightarrow{{}}{{C}_{2}}{{H}_{6}}(g)\] using the data given below \[{{C}_{2}}{{H}_{4}}(g)+3{{O}_{2}}(g)\xrightarrow{{}}2C{{O}_{2}}(g)+2{{H}_{2}}O(l)\] \[\Delta H=-1415\,kJ\] \[{{C}_{2}}{{H}_{6}}(g)+\frac{7}{2}{{O}_{2}}(g)\xrightarrow{{}}2C{{O}_{2}}(g)+3{{H}_{2}}O\] \[\Delta H=-1566\,kJ\] \[{{H}_{2}}(g)+\frac{1}{2}{{O}_{2}}(g)\xrightarrow{{}}{{H}_{2}}O(l);\Delta H=-286\,kJ\]
  A)
  \[-437\,kJ\]
  done clear
  B)
   \[135\,kJ\]
  done clear
  C)
   \[-135\,kJ\]
  done clear
  D)
   None of these
  done clear
  View Answer play_arrow

• question_answer96) In thermodynamics, a quantity whose value simply depends upon the initial and final state of the system is called
  A)
   a thermodynamic quantity
  done clear
  B)
   a state function
  done clear
  C)
   an adiabatic quantity
  done clear
  D)
   a path function
  done clear
  View Answer play_arrow

• question_answer97) All naturally occurring processes proceed spontaneously in a direction which leads to
  A)
   increase in enthalpy of system
  done clear
  B)
   decrease in entropy of system
  done clear
  C)
   decrease in free energy of system
  done clear
  D)
   increase in free energy of system
  done clear
  View Answer play_arrow

• question_answer98) When an electrolytic solution conducts electricity, the current is carried by
  A)
   the electrons
  done clear
  B)
   cations and anions
  done clear
  C)
   neutral molecules
  done clear
  D)
   the atoms of the electrolyte
  done clear
  View Answer play_arrow

• question_answer99) An electrochemical cell has two half cell reactions as, \[{{A}^{2+}}+2{{e}^{-}}\xrightarrow{{}}A;\]  \[E_{{{A}^{2+}}/A}^{o}=0.34\,V\] \[X\xrightarrow{{}}{{X}^{2+}}+2{{e}^{-}};\] \[E_{{{x}^{2}}/x}^{0}=-2.37\,V\] The cell voltage will be
  A)
  \[2.71\,V\]
  done clear
  B)
  \[2.03\,V\]
  done clear
  C)
   \[-2.71\,V\]
  done clear
  D)
  \[-2.03\,V\]
  done clear
  View Answer play_arrow

• question_answer100) In the electrolysis of dilute £[2804 using platinum electrode
  A)
  \[{{\text{H}}_{\text{2}}}\]is liberated at cathode
  done clear
  B)
  \[{{\text{O}}_{\text{2}}}\]is produced at cathode
  done clear
  C)
  \[\text{C}{{\text{l}}_{\text{2}}}\] is obtained at cathode
  done clear
  D)
  \[\text{N}{{\text{H}}_{\text{3}}}\] is produced at anode
  done clear
  View Answer play_arrow

• question_answer101) When a solution of sodium hydroxide is added to acetic acid solution, the conductivity of the resulting solution will
  A)
   increase          
  done clear
  B)
   remain unchanged
  done clear
  C)
   decrease          
  done clear
  D)
   become zero
  done clear
  View Answer play_arrow

• question_answer102) The behaviour of a real gas approaches ideal behaviour at
  A)
   low temperature, low pressure
  done clear
  B)
   high temperature, high pressure
  done clear
  C)
   low temperature, high pressure
  done clear
  D)
   high temperature, low pressure
  done clear
  View Answer play_arrow

• question_answer103) Which of the following is not the postulate of the kinetic theory of gases?
  A)
   Gas molecules are in a permanent state of random motion
  done clear
  B)
   Pressure of gas is due to molecular impacts on the walls
  done clear
  C)
   The molecules are perfectly elastic
  done clear
  D)
   The molecular collisions are elastic
  done clear
  View Answer play_arrow

• question_answer104) When a cation leaves its normal position in the crystal and moves to some interstitial space, the defect in the crystal is known as
  A)
   Schottky defect    
  done clear
  B)
   F-centre
  done clear
  C)
   Frenkel defect
  done clear
  D)
   non-stoichiometric defect
  done clear
  View Answer play_arrow

• question_answer105) Fog is a colloidal system of  
  A)
   gas in liquid        
  done clear
  B)
   liquid in gas
  done clear
  C)
   gas in gas          
  done clear
  D)
   gas in solid
  done clear
  View Answer play_arrow

• question_answer106) The purification of a colloidal solution could be done by
  A)
   sedimentation       
  done clear
  B)
   ultrafiltration
  done clear
  C)
   filtration         
  done clear
  D)
   precipitation
  done clear
  View Answer play_arrow

• question_answer107) Bakelite is a product of the reaction between
  A)
   formaldehyde and NaOH .
  done clear
  B)
   aniline and urea
  done clear
  C)
   phenol and methanol
  done clear
  D)
   phenol and chloroform
  done clear
  View Answer play_arrow

• question_answer108) How does electron affinity change when we move from left to right in a period in the Periodic Table?
  A)
   It increases
  done clear
  B)
   It decreases
  done clear
  C)
   It remains unchanged
  done clear
  D)
   It first increases and then decreases
  done clear
  View Answer play_arrow

• question_answer109) Which of the following statements is not correct?
  A)
   lonisation energy increases on going down a group in the Periodic Table
  done clear
  B)
   Among alkaline earth metals, reducing character increases down the group
  done clear
  C)
   Fluorine is the most electronegative element
  done clear
  D)
   Metallic character increases on going down a group in the Periodic Table
  done clear
  View Answer play_arrow

• question_answer110) Which of the following species has a trigonal planar shape?
  A)
  \[_{.}^{.}CH_{3}^{-}\]
  done clear
  B)
  \[CH_{3}^{+}\]
  done clear
  C)
   \[BF_{4}^{-}\]
  done clear
  D)
  \[Si{{H}_{4}}\]
  done clear
  View Answer play_arrow

• question_answer111) Which of the following will have maximum dipole moment?
  A)
   \[N{{F}_{3}}\]
  done clear
  B)
  \[N{{H}_{3}}\]
  done clear
  C)
  \[C{{H}_{4}}\]
  done clear
  D)
   \[PC{{l}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer112) Which of the following forces is the strongest?
  A)
   Hydrogen bonding 
  done clear
  B)
   Dipole-dipole forces
  done clear
  C)
   van der Waals' forces
  done clear
  D)
   Coordinate bonding
  done clear
  View Answer play_arrow

• question_answer113) Which of the following statements is correct?
  A)
  \[s{{p}^{3}}-\] hybrid orbitals have equal s and p character   
  done clear
  B)
   The bond angle decreases with the decrease of s character of a hybridized orbital
  done clear
  C)
   Resonance decreases the stability of a molecule
  done clear
  D)
   Resonance is due to delocalization of sigma electrons
  done clear
  View Answer play_arrow

• question_answer114)  Which of the following is the correct order of increasing oxidising character of oxoacids of chlorine?
  A)
   \[HCl{{O}_{3}}<HCl{{O}_{4}}<HCl{{O}_{2}}<HClO\]
  done clear
  B)
  \[~HCl{{O}_{4}}<HCl{{O}_{3}}<HCl{{O}_{2}}<HClO\]
  done clear
  C)
  \[~HClO<HCl{{O}_{4}}<HCl{{O}_{3}}<HCl{{O}_{2}}\]
  done clear
  D)
  \[HClO<HCl{{O}_{2}}<HCl{{O}_{3}}<HCl{{O}_{4}}\]
  done clear
  View Answer play_arrow

• question_answer115) Which of the following oxides of group 16 has the highest boiling point?
  A)
  \[{{H}_{2}}O\]
  done clear
  B)
  \[{{H}_{2}}S\]
  done clear
  C)
  \[{{H}_{2}}Se\]
  done clear
  D)
  \[{{H}_{2}}Te\]
  done clear
  View Answer play_arrow

• question_answer116) The +1 oxidation state of thallium is more stable than its +3 oxidation state because of
  A)
   its atomic size      
  done clear
  B)
   its ionization potential
  done clear
  C)
   inert pair effect     
  done clear
  D)
   diagonal relationship
  done clear
  View Answer play_arrow

• question_answer117) Which of the following statements is false regarding alkali metals?
  A)
   Alkali metals are soft and can be cut with the help of knife
  done clear
  B)
   Alkali metals do not occur in free state in nature
  done clear
  C)
   Alkali metals are highly electropositive elements
  done clear
  D)
   Alkali metal hydrides are covalent in character
  done clear
  View Answer play_arrow

• question_answer118) Among   the   following   outermost configurations of transition metals, which shows the highest oxidation state?
  A)
  \[~3{{d}^{3}}4{{s}^{2}}\]           
  done clear
  B)
  \[~3{{d}^{5}}\text{ }4{{s}^{1}}\]
  done clear
  C)
  \[3{{d}^{5}}\text{ }4{{s}^{2}}\]
  done clear
  D)
   \[3{{d}^{2}}\text{ }4{{s}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer119) The tendency of transition metals to form stable complexes is due to their
  A)
   low ionization energies
  done clear
  B)
   variable oxidation states
  done clear
  C)
   strong electropositive nature
  done clear
  D)
   high charge/size ratio and vacant d orbitals
  done clear
  View Answer play_arrow

• question_answer120) The transition metal ions are generally paramagnetic in nature because
  A)
   they have coloured salts
  done clear
  B)
   they have one or more unpaired cf-electrons
  done clear
  C)
   they have one or more paired s-electrons
  done clear
  D)
   they are reducing agents
  done clear
  View Answer play_arrow

• question_answer121) The most common oxidation state of lanthanides is
  A)
  \[+\,4\]                  
  done clear
  B)
   \[+\text{ }3\]
  done clear
  C)
  \[+\,6\]                 
  done clear
  D)
  \[+\,2\]
  done clear
  View Answer play_arrow

• question_answer122) Specify the coordination number of cobalt in \[[Co(CN)({{H}_{2}}O){{(en)}^{2}}]{{~}^{2+}}\]
  A)
   6       
  done clear
  B)
   4       
  done clear
  C)
   0       
  done clear
  D)
   3
  done clear
  View Answer play_arrow

• question_answer123) Which of the following complexes is square planar and diamagnetic?
  A)
   \[{{[NiC{{l}_{4}}]}^{2-}}\]
  done clear
  B)
  \[{{[NI{{(CN)}_{4}}]}^{2-}}\]
  done clear
  C)
   \[{{[Cr{{(N{{H}_{3}})}_{6}}]}^{3+}}\]
  done clear
  D)
   \[{{[CuC{{l}_{4}}]}^{2-}}\]
  done clear
  View Answer play_arrow

• question_answer124) Which type of isomerism is exhibited by\[[Pt{{(N{{H}_{3}})}_{2}}C{{l}_{2}}]?\]
  A)
   Coordination isomerism
  done clear
  B)
   Linkage isomerism
  done clear
  C)
   Optical isomerism
  done clear
  D)
   Geometrical isomerism
  done clear
  View Answer play_arrow

• question_answer125) Ethylene diamine tetraacetate ion is a
  A)
   unidentate ligand   
  done clear
  B)
   bidentate ligand
  done clear
  C)
   pentadentate ligand
  done clear
  D)
   hexadentate ligand
  done clear
  View Answer play_arrow

• question_answer126) Which of the following is an ore of zinc?
  A)
   Galena           
  done clear
  B)
   Pyrolusite
  done clear
  C)
   Sphaterite          
  done clear
  D)
   Magnetite
  done clear
  View Answer play_arrow

• question_answer127) The impurities associated with the ore after mining are collectively called
  A)
   flux                
  done clear
  B)
   slag
  done clear
  C)
   minerals            
  done clear
  D)
   gangue
  done clear
  View Answer play_arrow

• question_answer128) During extraction of iron, the iron obtained at the bottom of blast furnace is known as
  A)
   steel              
  done clear
  B)
   wrought iron
  done clear
  C)
   cast iron           
  done clear
  D)
   None of these
  done clear
  View Answer play_arrow

• question_answer129) Select the molecule which has only one \[\pi -\]bond                 
  A)
   \[CH\equiv CH\]
  done clear
  B)
   \[C{{H}_{2}}=CH-CHO\]
  done clear
  C)
   \[C{{H}_{3}}-CH=C{{H}_{2}}\]
  done clear
  D)
   \[C{{H}_{3}}-CH=CH-COOH\]
  done clear
  View Answer play_arrow

• question_answer130) Which of the following groups is ortho and para directing?
  A)
   \[-COCl\]
  done clear
  B)
   \[-CHO\]
  done clear
  C)
   \[-OH\]
  done clear
  D)
   \[-COC{{H}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer131) Amongst the given cations, the most stable carbonium ion is
  A)
   \[{{\,}^{+}}C{{H}_{3}}\]
  done clear
  B)
  \[{{(C{{H}_{3}})}_{3}}{{C}^{+}}\]
  done clear
  C)
   \[C{{H}_{3}}C{{H}_{2}}\]
  done clear
  D)
  \[{{(C{{H}_{3}})}_{2}}\overset{+}{\mathop{C}}\,H\]
  done clear
  View Answer play_arrow

• question_answer132) The hybridization of carbon atoms in C?C single bond of\[HC=C-CH=C{{H}_{2}}\] is
  A)
   \[s{{p}^{3}}-s{{p}^{2}}\]
  done clear
  B)
  \[s{{p}^{2}}-s{{p}^{3}}\]
  done clear
  C)
   \[sp-s{{p}^{2}}\]
  done clear
  D)
  \[s{{p}^{3}}-s{{p}^{3}}\]
  done clear
  View Answer play_arrow

• question_answer133) The number of optical isomers of the compound\[C{{H}_{3}}CHBrCHBrCOOH\]is
  A)
   0                      
  done clear
  B)
   1
  done clear
  C)
   3                     
  done clear
  D)
   4
  done clear
  View Answer play_arrow

• question_answer134) Electrolysis of an aqueous solution of sodium ethanoate gives
  A)
   methane           
  done clear
  B)
   ethane
  done clear
  C)
   butane            
  done clear
  D)
   methyl ethanoate
  done clear
  View Answer play_arrow

• question_answer135) Which of the following compounds will exhibit cis-trans (geometrical) isomerism?
  A)
   2-butene           
  done clear
  B)
   2-butyne
  done clear
  C)
   2-butanol          
  done clear
  D)
   1-butanol
  done clear
  View Answer play_arrow

• question_answer136) The reaction given below is an example of which of the following? \[2C{{H}_{3}}Br+2Na\xrightarrow{\text{dry}\,\text{ether}}{{C}_{2}}{{H}_{6}}+2NaBr\]
  A)
  Reimer-Tiemann reaction
  done clear
  B)
   Wurtz reaction                     
  done clear
  C)
   Hoffman bromamide reaction
  done clear
  D)
   Aldol condensation
  done clear
  View Answer play_arrow

• question_answer137) Chlorobenzene can be prepared by reacting aniline with
  A)
   hydrochloric acid in the presence of nitrous acid
  done clear
  B)
   cuprous chloride in the presence of  aluminium chloride
  done clear
  C)
   chlorine in the presence of aluminium chloride
  done clear
  D)
   nitrous acid followed by heating with cuprous chloride        
  done clear
  View Answer play_arrow

• question_answer138) Phenol on treatment with cone. \[\text{HN}{{\text{O}}_{\text{3}}}\]gives
  A)
   o-nitrophenol       
  done clear
  B)
   p-nitrophenol
  done clear
  C)
   o-and p-nitrophenol
  done clear
  D)
   2, 4, 6-trinitrophenol
  done clear
  View Answer play_arrow

• question_answer139) Which of the following compounds will be formed when methoxy benzene is reacted  with HBr?
  A)
   Phenol and bromomethane
  done clear
  B)
   Methanol and bromobenzene
  done clear
  C)
   Phenol and methanol
  done clear
  D)
   Bromobenzene and bromomethane
  done clear
  View Answer play_arrow

• question_answer140) When ethanol and\[{{\text{I}}_{\text{2}}}\]are heated in the presence of\[\text{N}{{\text{a}}_{\text{2}}}\text{C}{{\text{O}}_{\text{3}}}\text{,}\]the yellow crystals obtained are of
  A)
   \[{{C}_{2}}{{H}_{5}}l\]
  done clear
  B)
  \[C{{H}_{3}}l\]
  done clear
  C)
   \[CH{{l}_{3}}\]
  done clear
  D)
  \[C{{H}_{2}}{{l}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer141) Identify B in the following series of reaction \[C{{H}_{3}}CHO\xrightarrow{C{{H}_{3}}MgX}A\xrightarrow{HOH}B\]
  A)
   2-propanol         
  done clear
  B)
   1-propanol
  done clear
  C)
   ethanol          
  done clear
  D)
   None of these       
  done clear
  View Answer play_arrow

• question_answer142) Which of the following compounds has maximum acidic character?
  A)
   Dichloroacetic acid  
  done clear
  B)
   Acetic acid
  done clear
  C)
   Trichloroacetic ucid 
  done clear
  D)
   Triflouoroacetic acid
  done clear
  View Answer play_arrow

• question_answer143)  Among the following, the least reactive aldehyde is
  A)
   \[HCHO\]
  done clear
  B)
  \[{{C}_{6}}{{H}_{5}}CHO\]
  done clear
  C)
   \[C{{H}_{3}}CHO\]
  done clear
  D)
  \[{{C}_{2}}{{H}_{5}}CHO\]
  done clear
  View Answer play_arrow

• question_answer144) Propanal on reaction with lithium aluminium hydride gives
  A)
   1-propanol      
  done clear
  B)
   2-propanol
  done clear
  C)
   ethanol
  done clear
  D)
   butanol
  done clear
  View Answer play_arrow

• question_answer145) Idenitfy Z in the following sequence \[C{{H}_{3}}C{{H}_{2}}I\xrightarrow{KCN}X\xrightarrow{{{H}_{3}}{{O}^{+}}/{{H}_{2}}O}Y\] \[\xrightarrow[\Delta ]{{{H}_{3}}{{O}^{+}}/{{H}_{2}}O}Z\]
  A)
  \[C{{H}_{3}}COCl\]
  done clear
  B)
  \[C{{H}_{3}}CON{{H}_{2}}\]
  done clear
  C)
  \[C{{H}_{3}}COOH\]
  done clear
  D)
  \[C{{H}_{3}}C{{H}_{2}}COOH\]
  done clear
  View Answer play_arrow

• question_answer146) Treatment of aniline with bromine water produces
  A)
   2,4,6-tribromoaniline                
  done clear
  B)
   a mixture of ortho and para bromoaniline
  done clear
  C)
   bromobenzene
  done clear
  D)
   N-bromoaniline
  done clear
  View Answer play_arrow

• question_answer147) \[{{C}_{6}}{{H}_{5}}COCl\xrightarrow{N{{H}_{3}}}X\xrightarrow{{{P}_{2}}{{O}_{5}}}Y\xrightarrow[{{H}_{2}}]{Ni}Z\] The end product in the above sequence of reactions is
  A)
   benzole acid       
  done clear
  B)
   aniline
  done clear
  C)
   benzyl amine       
  done clear
  D)
   benzonitrile
  done clear
  View Answer play_arrow

• question_answer148) Which of the following is least reactive to nitration?
  A)
   Benzene          
  done clear
  B)
   Nitrobenzene
  done clear
  C)
   Chlorobenzene     
  done clear
  D)
   Aniline
  done clear
  View Answer play_arrow

• question_answer149) Nucleic acids are polymers of
  A)
   nucleotides
  done clear
  B)
   nucleosides
  done clear
  C)
   nuclei of heavy metals
  done clear
  D)
   proteins
  done clear
  View Answer play_arrow

• question_answer150) Which of the following enzymes helps in digestion of proteins?
  A)
   Invertase
  done clear
  B)
   Trypsin
  done clear
  C)
   Tryosinase
  done clear
  D)
   Urease
  done clear
  View Answer play_arrow

• question_answer151) The value of\[\cos \left( \frac{3\pi }{2}+x \right)\,\cos \,(2\pi +x)\left\{ \cot \left( \frac{3\pi }{2}-x \right)+\cot \,(2\pi +x) \right\}\]is
  A)
   \[0\]               
  done clear
  B)
   \[1\]
  done clear
  C)
   \[cos\text{ }x\]
  done clear
  D)
   \[sin\text{ }x\]
  done clear
  View Answer play_arrow

• question_answer152) If  \[\sin B=3\sin (2A+B),\] then \[2\tan A+\tan (A+B)\] is equal to
  A)
   \[0\]                   
  done clear
  B)
   \[-2\]
  done clear
  C)
   \[1\]                     
  done clear
  D)
   \[1\]
  done clear
  View Answer play_arrow

• question_answer153) If \[\theta =\frac{\pi }{{{2}^{n}}+1},\]  then the value of \[{{2}^{n}}\cos \theta \,\cos \,2\theta \,\cos \,{{2}^{2}}\theta .....\cos {{2}^{n-1}}\theta \] is
  A)
   \[\sin \theta \]
  done clear
  B)
   \[\frac{\pi }{2}\]
  done clear
  C)
   \[0\]
  done clear
  D)
   \[1\]
  done clear
  View Answer play_arrow

• question_answer154) Using the principal values, the value of \[{{\sin }^{-1}}\left\{ \sin \frac{5\pi }{6} \right\}+{{\tan }^{-1}}\left\{ \tan \frac{\pi }{6} \right\}\]is equal to
  A)
   \[\frac{\pi }{6}\]
  done clear
  B)
   \[\frac{2\pi }{3}\]
  done clear
  C)
   \[\frac{\pi }{3}\]
  done clear
  D)
   \[\frac{5\pi }{6}\]
  done clear
  View Answer play_arrow

• question_answer155) Find the value of \[{{\cos }^{-1}}\left( \frac{4}{5} \right)+{{\tan }^{-1}}\left( \frac{3}{5} \right)\].
  A)
   \[{{\tan }^{-1}}\left( \frac{7}{10} \right)\]
  done clear
  B)
   \[{{\tan }^{-1}}\left( \frac{27}{11} \right)\]
  done clear
  C)
   \[{{\sin }^{-1}}\left( \frac{7}{5} \right)\]
  done clear
  D)
   \[{{\tan }^{-1}}\left( \frac{1}{5} \right)\]
  done clear
  View Answer play_arrow

• question_answer156) If \[X+Y=\left[ \begin{matrix}    7 & 0  \\    2 & 5  \\ \end{matrix} \right]\] and \[X-Y=\left[ \begin{matrix}    3 & 0  \\    0 & 3  \\ \end{matrix} \right]\], then  X is equal to
  A)
   \[\left[ \begin{matrix}    5 & 0  \\    0 & 4  \\ \end{matrix} \right]\]
  done clear
  B)
   \[\left[ \begin{matrix}    7 & 0  \\    1 & 5  \\ \end{matrix} \right]\]
  done clear
  C)
   \[\left[ \begin{matrix}    5 & 0  \\    1 & 4  \\ \end{matrix} \right]\]
  done clear
  D)
   \[\left[ \begin{matrix}    7 & 1  \\    0 & 4  \\ \end{matrix} \right]\]
  done clear
  View Answer play_arrow

• question_answer157) If  \[\left| \begin{matrix}    x+7 & 5  \\    x+-3 & 3  \\ \end{matrix} \right|=26,\] then x is equal to
  A)
   \[1\]                   
  done clear
  B)
   \[3\]
  done clear
  C)
   \[5\]                   
  done clear
  D)
   \[7\]
  done clear
  View Answer play_arrow

• question_answer158) The value of \[\left| \begin{matrix}    {{a}^{2}} & 2ab & {{b}^{2}}  \\    {{b}^{2}} & {{a}^{2}} & 2ab  \\    2ab & {{b}^{2}} & {{a}^{2}}  \\ \end{matrix} \right|\] is
  A)
   \[{{({{a}^{2}}+{{b}^{2}})}^{3}}\]        
  done clear
  B)
   \[{{({{a}^{3}}+{{b}^{3}})}^{2}}\]
  done clear
  C)
   \[{{({{a}^{4}}+{{b}^{4}})}^{2}}\]
  done clear
  D)
   \[{{({{a}^{2}}+{{b}^{2}})}^{4}}\]
  done clear
  View Answer play_arrow

• question_answer159) If \[A=\left[ \begin{matrix}    3 & -4  \\    1 & -1  \\ \end{matrix} \right],\] then  \[(A-A')\] is equal to (where, A 'is transpose of matrix A)
  A)
   null matrix         
  done clear
  B)
   identity matrix
  done clear
  C)
   symmetric        
  done clear
  D)
   skew-symmetric
  done clear
  View Answer play_arrow

• question_answer160) If \[{{A}^{-1}}=\left[ \begin{matrix}    5 & -2  \\    -7 & 3  \\ \end{matrix} \right]\] and \[{{B}^{-1}}=\frac{1}{2}\left[ \begin{matrix}    9 & -7  \\    -8 & 6  \\ \end{matrix} \right],\] then \[{{(AB)}^{-1}}\] is equal to
  A)
   \[\left[ \begin{matrix}    47 & -39/2  \\    -41 & 17  \\ \end{matrix} \right]\]
  done clear
  B)
   \[\left[ \begin{matrix}    94 & -82  \\    -39 & 34  \\ \end{matrix} \right]\]
  done clear
  C)
   \[\left[ \begin{matrix}    -47 & 46  \\    39/2 & -17  \\ \end{matrix} \right]\]
  done clear
  D)
   \[\left[ \begin{matrix}    -47 & 39/2  \\    46 & -17  \\ \end{matrix} \right]\]
  done clear
  View Answer play_arrow

• question_answer161) The value of \[\underset{x\to 1}{\mathop{\lim }}\,\frac{x-1}{{{\log }_{e}}x}\] is
  A)
   \[1\]
  done clear
  B)
   \[0\]
  done clear
  C)
   Not defined         
  done clear
  D)
   \[-1\]
  done clear
  View Answer play_arrow

• question_answer162) \[\underset{x\to 0}{\mathop{\lim }}\,\,{{\left\{ \tan \left( \frac{\pi }{4}+x \right) \right\}}^{1/x}}\]is equal to
  A)
   \[e\]
  done clear
  B)
   \[{{e}^{2}}\]
  done clear
  C)
   \[1/e\]
  done clear
  D)
   \[1/{{e}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer163) The value of \[\underset{n\to \infty }{\mathop{\lim }}\,\,\,\left\{ \frac{1+2+3+....+n}{n+2}-\frac{n}{2} \right\}\] is
  A)
   \[\frac{1}{2}\]
  done clear
  B)
   \[1\]
  done clear
  C)
   \[-1\]
  done clear
  D)
   \[-\frac{1}{2}\]
  done clear
  View Answer play_arrow

• question_answer164) If \[y=1+\frac{x}{1!}+\frac{{{x}^{2}}}{2!}+\frac{{{x}^{3}}}{3!}.....,\]then \[\frac{dy}{dx}\] is equal to
  A)
   \[{{e}^{x}}\]
  done clear
  B)
   \[\sin \,x\]
  done clear
  C)
   \[y\]
  done clear
  D)
   \[x\]
  done clear
  View Answer play_arrow

• question_answer165) The value of \[\frac{d}{dx}({{x}^{n}}\,{{\log }_{a}}\,x{{e}^{x}})\] is
  A)
   \[{{e}^{x}}\,{{\log }_{a}}\,x+\frac{{{x}^{n-1}}}{{{\log }_{e}}\,a}\]
  done clear
  B)
   \[{{e}^{x}}{{x}^{n-1}}\,\left\{ x{{\log }_{a}}\,x+\frac{1}{{{\log }_{e}}\,a}+n\,{{\log }_{a}}x \right\}\]
  done clear
  C)
   \[n{{x}^{n-1}}\,{{\log }_{a}}\,x{{e}^{x}}\]
  done clear
  D)
   \[{{x}^{n}}\,{{\log }_{a}}x.{{e}^{x}}\]
  done clear
  View Answer play_arrow

• question_answer166) The interval in which the function \[f(x)=\sin x-\cos x,\,\,\,\,0\le x\le 2\pi \] is strictly decreasing, is
  A)
   \[0<x<\frac{3\pi }{4}\]
  done clear
  B)
   \[\frac{7\pi }{4}<x<2\pi \]
  done clear
  C)
   \[\frac{3\pi }{4}<x<\frac{7\pi }{4}\]      
  done clear
  D)
   \[0<x<\frac{7\pi }{4}\]
  done clear
  View Answer play_arrow

• question_answer167) The slope of normal to the curve \[y={{x}^{3}}+2x+6\] which is parallel to line \[x+14y+4=0\] is
  A)
   \[-\frac{1}{3}\]                  
  done clear
  B)
   \[-\frac{1}{14}\]
  done clear
  C)
   \[-4\]                   
  done clear
  D)
   \[-\frac{1}{2}\]
  done clear
  View Answer play_arrow

• question_answer168) The approximate value of \[{{(0.009)}^{1/3}}\] is
  A)
   \[0.2\]             
  done clear
  B)
   \[0.2083\]
  done clear
  C)
   \[0.0032\]             
  done clear
  D)
   \[0.0083\]
  done clear
  View Answer play_arrow

• question_answer169) If \[\left\{ \begin{matrix}    \frac{(1-\cos \,4x)}{{{x}^{2}}}, & if & x<0  \\    a, & if & x=0,  \\    \frac{\sqrt{x}}{\sqrt{(16+\sqrt{x})}-4}, & if & x>0  \\ \end{matrix} \right.\]then \[f(x)\] is continuous at \[x=0,\] for a
  A)
   \[4\]      
  done clear
  B)
   \[\sqrt{32}\]
  done clear
  C)
   \[8\]      
  done clear
  D)
   \[16\]
  done clear
  View Answer play_arrow

• question_answer170) The value of \[\int_{0}^{\pi /2}{\frac{dx}{1+\tan x}}\] is
  A)
   \[\frac{\pi }{2}\]                     
  done clear
  B)
   \[0\]
  done clear
  C)
   \[\frac{\pi }{4}\]                     
  done clear
  D)
   \[\frac{\pi }{8}\]
  done clear
  View Answer play_arrow

• question_answer171) Evaluate \[\int{\frac{3x-2}{(x+3){{(x+1)}^{2}}}}\,dx.\]
  A)
   \[\frac{11}{4}\log \,[|x+1|\,|x+3|]+\frac{5}{2(x+1)}+C\]
  done clear
  B)
   \[\frac{11}{4}\log \,\left| \frac{x+3}{x+1} \right|+\frac{1}{x+1}+C\]
  done clear
  C)
   \[\frac{11}{4}\log \,|x+2|+\frac{5}{2}(x+3)+\frac{1}{x+1}+C\]
  done clear
  D)
   \[\frac{11}{4}\log \,\left| \frac{x+1}{x+3} \right|+\frac{5}{2(x+1)}+C\]
  done clear
  View Answer play_arrow

• question_answer172) The general solution of the linear differential equation \[\frac{dy}{dx}+\sec \,x.\,y=\tan x\] \[\left( 0\le x\le \frac{\pi }{2} \right)\]is
  A)
   \[y=-x\,{{(\sec x+\tan x)}^{-1}}+\frac{C}{\sec x+\tan x}+1\]
  done clear
  B)
   \[y=x+\frac{C}{\sec x+\tan x}+\frac{1}{\tan x}\]
  done clear
  C)
   \[y=\frac{x+1}{\sec x+\tan x}+C\]
  done clear
  D)
   \[y=x+\sec x-\tan \,x+C\]
  done clear
  View Answer play_arrow

• question_answer173) On solving the differential equation \[{{x}^{2}}y\,dx-({{x}^{3}}+{{y}^{2}})dy=0,\]the value of \[\log \,y\] is
  A)
   \[\frac{{{x}^{3}}}{3{{y}^{3}}}+C\]
  done clear
  B)
   \[\frac{{{x}^{2}}}{{{y}^{2}}}+C\]
  done clear
  C)
   \[\frac{{{x}^{2}}}{3{{y}^{3}}}+C\]
  done clear
  D)
   \[\frac{{{x}^{3}}}{{{x}^{3}}+{{y}^{3}}}+C\]
  done clear
  View Answer play_arrow

• question_answer174) The value of \[\int{\frac{2+\sin x}{1+\cos x}}\,{{e}^{x/2}}dx\] is
  A)
   \[2.{{e}^{x/2}}\,\tan \frac{x}{2}+C\]
  done clear
  B)
   \[{{e}^{x/2}}\,\tan \,x+C\]
  done clear
  C)
   \[\frac{1}{2}{{e}^{x/2}}\,\sin x+C\]
  done clear
  D)
   \[\frac{1}{2}\,\,{{e}^{x/2}}\,\sin \frac{x}{2}+C\]  
  done clear
  View Answer play_arrow

• question_answer175) On evaluation, the value of  \[\int_{0}^{4}{f(x)\,\,dx,}\]where  \[f(x)=\left\{ \begin{matrix}    |x-2|+2, & x\le 2  \\    {{x}^{2}}-2, & x>2  \\ \end{matrix} \right.\]  is
  A)
   \[\frac{56}{3}\]     
  done clear
  B)
   \[\frac{60}{3}\]
  done clear
  C)
   \[\frac{66}{3}\]     
  done clear
  D)
   \[\frac{62}{3}\]
  done clear
  View Answer play_arrow

• question_answer176) The particular solution of the differential equation \[\frac{dy}{dx}+y\,\cot \,x=2x+{{x}^{2}}\,\cot \,x,\]such that \[y(\pi /2)=0\]  is
  A)
   \[y=\frac{{{\pi }^{2}}}{4\,\cos \,x},(x\ne 0)\]
  done clear
  B)
   \[y={{x}^{2}}-\frac{\pi }{2}\tan x\]
  done clear
  C)
   \[y=\frac{2x}{\sin x}+\frac{1}{{{x}^{2}}},(x\ne 0)\]
  done clear
  D)
   \[y={{x}^{2}}-\frac{{{\pi }^{2}}}{4\sin x}(\sin x\ne 0)\]
  done clear
  View Answer play_arrow

• question_answer177) The differential equation corresponding to the equation\[{{y}^{2}}=a(b-{{x}^{2}})\] where a, b are constants is
  A)
   \[{{y}^{2}}\frac{{{d}^{2}}y}{d{{x}^{2}}}=a\left( b-\frac{dy}{dx}+x \right)\]
  done clear
  B)
   \[xy\frac{{{d}^{2}}y}{d{{x}^{2}}}+x{{\left( \frac{dy}{dx} \right)}^{2}}-y\frac{dy}{dx}=0\]
  done clear
  C)
   \[y{{\left( \frac{dy}{dx} \right)}^{2}}-x\frac{dy}{dx}+1=0\]
  done clear
  D)
   None of the above
  done clear
  View Answer play_arrow

• question_answer178) The area bounded by the circle \[{{x}^{2}}+{{y}^{2}}=16\] and the line \[y=x\]in the first quadrant is
  A)
   \[4\pi \,\,\,sq\,units\]         
  done clear
  B)
   \[8\pi \,\,\,sq\,units\]
  done clear
  C)
   \[2\pi \,\,\,sq\,units\]         
  done clear
  D)
   \[\pi \,\,\,sq\,units\]
  done clear
  View Answer play_arrow

• question_answer179) The focal distance of the point \[(x,y)\] from the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1,\,\,\,\,a>b\] is
  A)
   \[a\pm \sqrt{1-\frac{{{b}^{2}}}{{{a}^{2}}}}y\]
  done clear
  B)
   \[b\pm \sqrt{1-\frac{{{a}^{2}}}{{{b}^{2}}}}y\]
  done clear
  C)
   \[a\pm \sqrt{1-\frac{{{b}^{2}}}{{{a}^{2}}}}\,x\]
  done clear
  D)
   \[b\pm \sqrt{1-\frac{{{a}^{2}}}{{{b}^{2}}}}\,x\]
  done clear
  View Answer play_arrow

• question_answer180) The lines \[3x+y-14=0\] \[\lambda x-2y=0\] \[3x-8y+4=0\] are concurrent. Then, the value of \[\lambda \] is
  A)
   \[1\]                     
  done clear
  B)
   \[2\]
  done clear
  C)
   \[3\]                   
  done clear
  D)
   \[4\]
  done clear
  View Answer play_arrow

• question_answer181) The equation of a straight line which cuts off intercept on X-axis which is twice that on y-axis and is at a unit distance from . origin is given by
  A)
   \[x+y=0\]
  done clear
  B)
   \[x+2y\pm \sqrt{2}=0\]
  done clear
  C)
   \[x+2y\pm \sqrt{5}=0\]
  done clear
  D)
   \[x+\sqrt{5}y\pm 2=0\]
  done clear
  View Answer play_arrow

• question_answer182) The equation of a straight line upon which the length of the perpendicular from the origin is 5 and slope of this perpendicular is \[3/4\] is
  A)
   \[2x+5y\pm 16=0\]
  done clear
  B)
   \[4x+3y\pm 25=0\]
  done clear
  C)
   \[4x+3y\pm 5=0\]
  done clear
  D)
   \[2x+5y\pm 4=0\]
  done clear
  View Answer play_arrow

• question_answer183) The radius of the circle \[{{(x\,\cos \theta +y\sin \theta -a)}^{2}}+(x\,\sin \theta -y\cos \theta )={{k}^{2}}\] is
  A)
   \[{{a}^{2}}+{{b}^{2}}-{{k}^{2}}\]
  done clear
  B)
   \[a\,sin\,\theta -b\,\cos \,\theta \]
  done clear
  C)
   \[{{a}^{2}}+{{b}^{2}}\]
  done clear
  D)
   \[k\]
  done clear
  View Answer play_arrow

• question_answer184) The locus of a point which moves in a plane such that its distance from a fixed point in the plane is always equal to its distance from a fixed straight line in the same plane represents
  A)
   a circle             
  done clear
  B)
   a parabola
  done clear
  C)
   a hyperbola        
  done clear
  D)
   an ellipse
  done clear
  View Answer play_arrow

• question_answer185) The   eccentricity   of   the   ellipse \[25{{x}^{2}}+9{{y}^{2}}-150x-90y+225=0\]is
  A)
   \[\frac{4}{5}\]
  done clear
  B)
   \[\frac{3}{5}\]
  done clear
  C)
   \[\frac{4}{15}\]
  done clear
  D)
   \[\frac{9}{5}\]
  done clear
  View Answer play_arrow

• question_answer186) The mean deviation from the median is
  A)
   equal to that measured from another value
  done clear
  B)
   maximum, if all observations are positive
  done clear
  C)
   greater than that measured from any other value
  done clear
  D)
   less than measured from any other value
  done clear
  View Answer play_arrow

• question_answer187) The variance of the data      

  \[x:1\]	\[a\]	\[{{a}^{2}}\]	?..	\[{{a}^{n}}\]
  \[f{{:}^{n}}{{C}_{0}}\]	\[^{n}{{C}_{1}}\]	\[^{n}{{C}_{2}}\]	?..	\[^{n}{{C}_{n}}\]

  A)
   \[{{\left( \frac{1+{{a}^{2}}}{2} \right)}^{n}}-{{\left( \frac{1+a}{2} \right)}^{2n}}\]
  done clear
  B)
   \[{{\left( \frac{1+{{a}^{2}}}{2} \right)}^{2n}}-{{\left( \frac{1+a}{2} \right)}^{n}}\]
  done clear
  C)
   \[{{\left( \frac{1+a}{2} \right)}^{2n}}-{{\left( \frac{1+{{a}^{2n}}}{2} \right)}^{n}}\]
  done clear
  D)
   \[{{\left( \frac{1+a}{2} \right)}^{n}}-{{\left( \frac{1+{{a}^{2n}}}{2} \right)}^{n}}\]            
  done clear
  View Answer play_arrow

• question_answer188) An analysis of the weekly wages paid to workers in two firms A and B, belonging to the same industry gives the following results

  	Firm A	Firm B
  Number of wage earners	\[586\]	\[648\]
  Average of weekly wages	Rs. \[52.5\]	Rs. \[47.5\]
  Variance of the distribution of wages	\[100\]	\[121\]

  Then, which firm pays out larger amount and which shows greater variability, respectively?
  A)
   \[A,\,B\]    
  done clear
  B)
   \[B,\,A\]    
  done clear
  C)
   \[B,\,B\]    
  done clear
  D)
   \[A,\,A\]
  done clear
  View Answer play_arrow

• question_answer189) If the standard deviation of a variable X is \[\sigma ,\] then the standard deviation of variable \[\frac{aX+b}{c}\]is
  A)
   \[a\sigma \]
  done clear
  B)
   \[\frac{a}{c}\sigma \]
  done clear
  C)
   \[\left| \frac{a}{c} \right|\sigma \]
  done clear
  D)
   \[\frac{a\sigma +b}{c}\]
  done clear
  View Answer play_arrow

• question_answer190) A bag contains 50 tickets numbered 1, 2, 3, ...,50 of which five are drawn at random and arranged in ascending order of magnitude \[({{x}_{1}}<{{x}_{2}}<{{x}_{3}}<{{x}_{4}}<{{x}_{5}}),\] then the probability that \[{{x}_{3}}=30\] is
  A)
   \[\frac{^{29}{{C}_{2}}{{\times }^{20}}{{C}_{2}}}{^{50}{{C}_{5}}}\]
  done clear
  B)
   \[\frac{^{30}{{C}_{1}}{{\times }^{29}}{{C}_{1}}}{^{50}{{C}_{5}}}\]
  done clear
  C)
   \[\frac{^{5}{{C}_{1}}{{\times }^{50}}{{C}_{2}}}{^{50}{{C}_{5}}}\]
  done clear
  D)
   \[\frac{^{50}{{C}_{2}}{{\times }^{29}}{{C}_{1}}}{^{50}{{C}_{5}}}\]
  done clear
  View Answer play_arrow

• question_answer191) If S is the sample space and \[P(A)=\frac{1}{3}\,P(B)\]and \[S=A\cup B,\] where A and B are two mutually exclusive events, then \[P(A)\] is equal to
  A)
   \[\frac{1}{4}\]                   
  done clear
  B)
   \[\frac{1}{2}\]
  done clear
  C)
   \[\frac{3}{4}\]
  done clear
  D)
   \[\frac{3}{8}\]
  done clear
  View Answer play_arrow

• question_answer192) Five persons entered the lift cabin on the ground floor of an eight floor house. Suppose that each of them independently and with equal probability can leave the cabin at any floor beginning with the first, then the probability of all 5 persons leaving at different floors is
  A)
   \[\frac{^{7}{{P}_{5}}}{{{7}^{5}}}\]
  done clear
  B)
   \[\frac{{{7}^{5}}}{^{7}{{P}_{5}}}\]
  done clear
  C)
   \[\frac{6}{^{6}{{P}_{5}}}\]
  done clear
  D)
   \[\frac{^{5}{{P}_{5}}}{{{5}^{5}}}\]
  done clear
  View Answer play_arrow

• question_answer193) In a three dimensional space the equation \[{{x}^{2}}-5x+6=0\]represents
  A)
   points             
  done clear
  B)
   planes
  done clear
  C)
   curves             
  done clear
  D)
   None of these
  done clear
  View Answer play_arrow

• question_answer194) If \[(3,\,4,-1)\] and \[(-1,\,2,3)\] be end points of the diameter of a sphere, then the radius of the sphere is
  A)
   \[2\]                     
  done clear
  B)
   \[3\]
  done clear
  C)
   \[6\]                     
  done clear
  D)
   \[7\]
  done clear
  View Answer play_arrow

• question_answer195) If the position vector a of a point \[(12,\,\,n)\] is such that \[|a|=13,\] then the value of \[\pi \] is
  A)
   \[\pm \,\,3\]                   
  done clear
  B)
   \[\pm \,\,4\]
  done clear
  C)
   \[\pm \,\,5\]                   
  done clear
  D)
   \[\pm \,\,6\]
  done clear
  View Answer play_arrow

• question_answer196) The following lines are \[r=(\hat{i}+\hat{j})+\lambda (\hat{i}+2\hat{j}-\hat{k}),\] and \[r=(\hat{i}+\hat{j})+\mu (-\hat{i}+\hat{j}-2\hat{k})\]
  A)
   collinear            
  done clear
  B)
   skew-lines
  done clear
  C)
   coplanar lines       
  done clear
  D)
   parallel lines
  done clear
  View Answer play_arrow

• question_answer197) The position vector of a point R which divides the line joining \[P(6,\,3,-2)\]and \[Q(3,1,-4)\]Q(3,1, - 4) in the ratio \[2:1\] externally is
  A)
   \[\hat{i}+3\hat{j}-2\hat{k}\]     
  done clear
  B)
   \[3\hat{i}-\hat{k}\]
  done clear
  C)
   \[-\hat{j}-6\hat{k}\]         
  done clear
  D)
   \[2\hat{i}-\hat{j}\]
  done clear
  View Answer play_arrow

• question_answer198) If \[a=\hat{i}+2\hat{j}-3\hat{k}\] and \[b=2\hat{i}+4\hat{j}+9\hat{k},\] then the unit vector parallel to \[a+b\] is
  A)
   \[\frac{1}{6}\,5\hat{i}-\hat{k}\]
  done clear
  B)
   \[\frac{1}{\sqrt{35}}(5\hat{i}+3\hat{j}-\hat{k})\]
  done clear
  C)
   \[\frac{1}{5}(3\hat{j}-5\hat{k})\]
  done clear
  D)
   \[3\hat{i}+6\hat{j}-6\hat{k}\]
  done clear
  E)
   None of these
  done clear
  View Answer play_arrow

• question_answer199) The   angle   between   the   lines \[\frac{x-5}{-3}=\frac{y+3}{-4}=\frac{z-7}{0},\,\frac{x}{1}=\frac{y-1}{-2}=\frac{z-6}{2}\]is
  A)
   \[\frac{\pi }{3}\]
  done clear
  B)
   \[{{\tan }^{-1}}\left( \frac{1}{5} \right)\]
  done clear
  C)
   \[{{\cos }^{-1}}\left( \frac{1}{3} \right)\]
  done clear
  D)
   \[\frac{\pi }{2}\]
  done clear
  View Answer play_arrow

• question_answer200) If \[|a|=2,\,\,|b|=5\]  and \[|a\times b|=8,\] then \[a\,.\,b\] is equal to      
  A)
   \[3\]                     
  done clear
  B)
   \[4\]
  done clear
  C)
   \[5\]                      
  done clear
  D)
   \[6\]
  done clear
  View Answer play_arrow

• question_answer201) Suppose \[{{A}_{1}},{{A}_{2}}.....,{{A}_{30}}\]are thirty sets each  with five elements and \[{{B}_{1}},{{B}_{2}}.....,{{B}_{n}}\] are 'n' sets each with three elements. Let     \[\underset{i=1}{\mathop{\overset{30}{\mathop{\cup }}\,}}\,\,\,{{A}_{i}}=\underset{j=1}{\mathop{\overset{n}{\mathop{\cup }}\,}}\,\,\,\,{{B}_{j}}=S.\] Assume that each element of S belongs to exactly 10 of \[{{A}_{i}}s\] and exactly 9 of \[{{B}_{j}}s,\]then the value of x is
  A)
   \[90\]                  
  done clear
  B)
   \[15\]
  done clear
  C)
   \[9\]                 
  done clear
  D)
   45
  done clear
  View Answer play_arrow

• question_answer202) A survey shows that 63% of the Americans like cheese whereas 76% like apples. If x% of the Americans like both cheese and apples, then the value of x is
  A)
   \[39\le x\le 63\]       
  done clear
  B)
   \[63\]
  done clear
  C)
   \[39\]              
  done clear
  D)
   \[139\ge x\]
  done clear
  View Answer play_arrow

• question_answer203) The cartesian product \[A\times A\] has 9 elements among which are found \[(-1,0)\] and \[(0,1),\] then set A is equal to
  A)
   \[\{1,\,\,0\}\]             
  done clear
  B)
   \[\{1,\,\,-1,\,\,\,0\}\]
  done clear
  C)
   \[\{\,0,\,\,-1\}\]           
  done clear
  D)
   \[\{1,\,\,-1\}\]
  done clear
  View Answer play_arrow

• question_answer204) If \[S=\{(a,\,b):b=|a-1|,a\in Z\] and \[|a|<3\},\] where Z denotes the set of integers. Then, the range set of S is
  A)
   \[\{1,\,2,\,3\}\]            
  done clear
  B)
   \[\{-1,\,2,\,3,\,1\}\]
  done clear
  C)
   \[\{0,\,1,\,2,\,3,\,4\}\]
  done clear
  D)
   \[\{-\,1,-\,2,-\,3,-\,4\}\]
  done clear
  View Answer play_arrow

• question_answer205) Pisa relation from \[\{11,\,12,\,13\}\]to \[\{8,\,10,\,12\}\] defined by \[y=x-3\]. Then, \[{{R}^{-1}}\] is
  A)
   \[\{(8,\,11),\,(10,13)\}\]
  done clear
  B)
   \[\{(11,\,8),\,(13,10)\}\]
  done clear
  C)
   \[\{(10,\,13),\,(8,11),\,(12,\,10)\}\]
  done clear
  D)
   None of the above
  done clear
  View Answer play_arrow

• question_answer206) The quotient of the identity function by the reciprocal function is given by
  A)
   \[{{x}^{2}}\,\forall \,\,x\,\in \,R\] (set of real numbers)
  done clear
  B)
   \[\frac{1}{{{x}^{2}}}\,\,\forall \,\,x\in R-\{0\}\]
  done clear
  C)
   \[{{x}^{2}}\,\,\forall \,\,x\in R-\{0\}\]
  done clear
  D)
   None of the above
  done clear
  View Answer play_arrow

• question_answer207) Which of the following is not a function?
  A)
   \[\{(x,y):\,x,\,y\,\in R,{{x}^{2}}=y\}\]
  done clear
  B)
   \[\{(x,y):\,x,\,y\,\in R,{{y}^{2}}=x\}\]
  done clear
  C)
   \[\{(x,y):\,x,\,y\,\in R,x={{y}^{3}}\}\]
  done clear
  D)
   \[\{(x,y):\,x,\,y\,\in R,y={{x}^{3}}\}\]
  done clear
  View Answer play_arrow

• question_answer208) If \[(1+i)\,(2i+1)\,(1+3i)....(1+ni)=x+iy,\] then \[2.5.10....(1+{{n}^{2}})\] is equal to
  A)
   \[1\]
  done clear
  B)
   \[i\]
  done clear
  C)
   \[{{x}^{2}}+{{y}^{2}}\]
  done clear
  D)
   \[1+{{n}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer209) The value of \[|{{z}_{1}}|=|{{z}_{2}}|=...=|{{z}_{n}}|=1,\] then \[|{{z}_{1}}+{{z}_{2}}+{{z}_{3}}+....+{{z}_{n}}|\] is (where, \[{{z}_{1}}\] is complex number with \[i=1\] to n)
  A)
   \[\left| \frac{1}{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}+....+{{z}_{n}}} \right|\]
  done clear
  B)
   \[\left| \frac{1}{{{z}_{1}}}+\frac{1}{{{z}_{2}}}+\frac{1}{{{z}_{3}}}+...+\frac{1}{{{z}_{n}}} \right|\]
  done clear
  C)
   \[\left| \frac{1}{{{z}_{1}}{{z}_{2}}}+\frac{1}{{{z}_{3}}{{z}_{4}}}+....+\frac{1}{{{z}_{n-1}}{{z}_{n}}} \right|\]
  done clear
  D)
   \[1\]
  done clear
  View Answer play_arrow

• question_answer210) The non-zero solutions of the equation \[{{z}^{2}}+|z|=0,\] where z is a complex number, are
  A)
   \[\pm \,\,1\]
  done clear
  B)
   \[\pm \,\,i\]
  done clear
  C)
   \[1\pm \,\,i\]
  done clear
  D)
    \[\pm \,\,1\pm i\]
  done clear
  View Answer play_arrow

• question_answer211) Which of the following shaded regions  represents the solution set of in equation \[|x-y|\ge 1\]
  A)
   
  done clear
  B)
   
  done clear
  C)
   
  done clear
  D)
   
  done clear
  View Answer play_arrow

• question_answer212) The values of x for which \[-11\le 4x-3\le 13\]is
  A)
   \[-4\le x\le 5\]
  done clear
  B)
   \[-2\le x\le 4\]
  done clear
  C)
   \[-8\le x\le 16\]
  done clear
  D)
   \[-11\le x\le 10\]
  done clear
  View Answer play_arrow

• question_answer213) The solution set of the following linear in equations \[x-2y\ge 0;\,\,\,2x-y\le -2;\,\,x\ge 0,y\ge 0\]is given by
  A)
   \[[1,\,\,2]\]              
  done clear
  B)
   Null set
  done clear
  C)
   \[x\ge 1\]               
  done clear
  D)
   Set of real numbers
  done clear
  View Answer play_arrow

• question_answer214) For the given LPP (Linear Programming Problem) max \[z=5x+3y\] \[2x+y\le 12\] \[3x+2y\le 20\] \[x\ge 0,\,y\ge 0\] the optimal solution set is
  A)
   \[(0,\,\,0)\]              
  done clear
  B)
   \[(6,\,\,0)\]
  done clear
  C)
   \[(4,\,\,4)\]              
  done clear
  D)
   \[(0,\,\,10)\]
  done clear
  View Answer play_arrow

• question_answer215) A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains atleast 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin content of 1 kg food is given below

  Food	Vitamin A	Vitamin B	Vitamin C
  x	1	2	3
  y	2	2	1

  \[1\text{ }kg\]of food X costs \[Rs.\text{ }16\]and \[1\text{ }kg\] of food Y costs \[Rs.\text{ }20\]. Find the least cost of the mixture which will produce the required diet.
  A)
   \[Rs.\,100\]
  done clear
  B)
   \[Rs.\,98\]
  done clear
  C)
   \[Rs.\,116\]
  done clear
  D)
   \[Rs.\,112\]
  done clear
  View Answer play_arrow

• question_answer216) Which of the following is a purely imaginary term of the sequence \[8-6i,\] \[7-4i,\,6-2i,...\]?
  A)
   9th term                                 
  done clear
  B)
   2nd term
  done clear
  C)
   4th term            
  done clear
  D)
   8 term
  done clear
  View Answer play_arrow

• question_answer217) If \[{{S}_{n}}\] denotes the sum of first n terms of AP \[<{{a}_{n}}>,\]such that \[\frac{{{S}_{m}}}{{{S}_{n}}}=\frac{{{m}^{2}}}{{{n}^{2}}},\] then \[\frac{{{a}_{m}}}{{{a}_{n}}}\] is equal to
  A)
   \[\frac{2m+1}{2n+1}\]
  done clear
  B)
   \[\frac{2m-1}{2n-1}\]
  done clear
  C)
   \[\frac{m-1}{n-1}\]
  done clear
  D)
   \[\frac{m+1}{n+1}\]
  done clear
  View Answer play_arrow

• question_answer218) The sum of all possible products of the first n natural numbers taken two by two is
  A)
   \[\frac{n(n+1)}{2}\]
  done clear
  B)
   \[\frac{n(n+1)(n+2)}{6}\]
  done clear
  C)
   \[\frac{n({{n}^{2}}-1)(3n+2)}{12}\]
  done clear
  D)
   \[2{{n}^{3}}+3{{n}^{2}}-1\]
  done clear
  View Answer play_arrow

• question_answer219) How many four digit numbers are there with distinct digits?
  A)
   \[5040\]              
  done clear
  B)
   \[4536\]
  done clear
  C)
   \[30240\]             
  done clear
  D)
   \[5274\]
  done clear
  View Answer play_arrow

• question_answer220) If \[^{n}{{C}_{r}}{{+}^{n}}{{C}_{r+1}}{{=}^{n+1}}{{C}_{x}},\]then x is equal to
  A)
   \[r\]                 
  done clear
  B)
   \[r-1\]
  done clear
  C)
   \[n\]                
  done clear
  D)
   \[r+1\]
  done clear
  View Answer play_arrow

• question_answer221) The coefficient of the term independent of x in the expansion \[\left( \frac{x+1}{{{x}^{2/3}}-{{x}^{1/3}}+1}-\frac{x-1}{x-{{x}^{1/2}}} \right)\]is
  A)
   \[8064\]              
  done clear
  B)
   \[210\]
  done clear
  C)
   \[-546\]              
  done clear
  D)
   \[5040\]
  done clear
  View Answer play_arrow

• question_answer222) There are 12 points in a plane. The number of straight lines joining any two of them, when 3 of them are collinear, is
  A)
   \[60\]                
  done clear
  B)
   \[63\]
  done clear
  C)
   \[64\]                 
  done clear
  D)
   \[65\]
  done clear
  View Answer play_arrow

• question_answer223) Which of the following is the correct principle of Mathematical induction?
  A)
   Let \[P(n)\] be a statement such that n be any integer and \[P(1)\] is true. Also. \[P(m)\] is true for m, any natural number, then \[P(n)\] is true for all  integers n
  done clear
  B)
   Let \[P(n)\] be a statement involving natural number n such that \[P(1)\] is true and\[P(m)\]  is true whenever \[P(n)\] is true for every \[n\ge m,\]then \[P(n)\] is true for all \[n\in N\] (set of natural numbers)
  done clear
  C)
   Let\[P(n)\] be a statement where \[n\in N\]such that\[P(1)\] is true and \[P(n),\,P(n+1)\]also holds, then \[P(n)\] is true \[\forall n\in N\]
  done clear
  D)
   Let \[P(n)\] be a statement involving the natural number n, such trial P(1) is true and s\[P(m+1)\] is true for all \[n\le m\]Then, \[P(n)\] is true for all \[n\in N\]
  done clear
  View Answer play_arrow

• question_answer224) If \[x>0\]and \[{{\cot }^{-1}}\,(x+2)=\frac{\pi }{12},\] then the value of x is
  A)
   \[2\sqrt{3}\]
  done clear
  B)
   \[\sqrt{3}\]
  done clear
  C)
   \[\frac{1}{\sqrt{3}}\]
  done clear
  D)
   \[\sqrt{3}-1\]
  done clear
  View Answer play_arrow

• question_answer225) If \[\cot \,\theta (1+\sin \theta )=4m\] and \[\cot \theta (1-\sin \theta )=4n,\] then \[{{({{m}^{2}}-{{n}^{2}})}^{2}}\]is equal to
  A)
   \[mn\]
  done clear
  B)
   \[\tan \theta \]
  done clear
  C)
   \[1\]
  done clear
  D)
   \[\frac{m+n}{4}\]
  done clear
  View Answer play_arrow