question_answer 1) Two sound waves of slightly different frequencies propagating in the same direction produce beats due to
A)
interference
done
clear
B)
diffraction
done
clear
C)
reflection
done
clear
D)
refraction
done
clear
View Answer play_arrow
question_answer 2) An ice block floats in a liquid whose density is less than water. A part of block is outside the liquid. When whole of ice has melted, the liquid level will
A)
rise
done
clear
B)
go down
done
clear
C)
remain same
done
clear
D)
first rise then go down
done
clear
View Answer play_arrow
question_answer 3) Two bodies of different masses of 2 kg and 4 kg moving with velocities 2 m/s and 10 m/s towards each other due to mutual gravitational attraction. What is the velocity of their centre of mass?
A)
5 m/s
done
clear
B)
6 m/s
done
clear
C)
8 m/s
done
clear
D)
Zero
done
clear
View Answer play_arrow
question_answer 4) Given that the displacement of an oscillating particle is given by\[y=A\text{ }sin(Bx+Ct+D)\]. The dimensional formula for (ABCD) is
A)
\[[{{M}^{0}}{{L}^{-1}}{{T}^{0}}]\]
done
clear
B)
\[[{{M}^{0}}{{L}^{0}}{{T}^{-1}}]\]
done
clear
C)
\[[{{M}^{0}}{{L}^{-1}}{{T}^{-1}}]\]
done
clear
D)
\[[{{M}^{0}}{{L}^{0}}{{T}^{0}}]\]
done
clear
View Answer play_arrow
question_answer 5) Two waves having intensities in the ratio of \[9:1\]produce interference. The ratio of maximum to minimum intensity is equal to
A)
\[10:8\]
done
clear
B)
\[9:1\]
done
clear
C)
\[4:1\]
done
clear
D)
\[2:1\]
done
clear
View Answer play_arrow
question_answer 6) If a magnet is suspended at angle\[30{}^\circ \]to the magnetic meridian, the dip needle makes an angle of\[45{}^\circ \]with the horizontal. The real dip is
A)
\[{{\tan }^{-1}}(\sqrt{3/2})\]
done
clear
B)
\[{{\tan }^{-1}}(\sqrt{3})\]
done
clear
C)
\[{{\tan }^{-1}}(\sqrt{2/3})\]
done
clear
D)
\[{{\tan }^{-1}}(2/\sqrt{3})\]
done
clear
View Answer play_arrow
question_answer 7) A radioactive element has half-life period of 600 years. After 3000 years, what amount will remain?
A)
\[\frac{1}{2}\]
done
clear
B)
\[\frac{1}{16}\]
done
clear
C)
\[\frac{1}{8}\]
done
clear
D)
\[\frac{1}{32}\]
done
clear
View Answer play_arrow
question_answer 8) Beyond which frequency, the ionosphere bends any incident electromagnetic radiation but do not reflect it back towards the earth?
A)
50MHz
done
clear
B)
40MHz
done
clear
C)
30 MHz
done
clear
D)
20 MHz
done
clear
View Answer play_arrow
question_answer 9) In intrinsic semiconductor at room temperature number of electrons and holes are
A)
equal
done
clear
B)
zero
done
clear
C)
unequal
done
clear
D)
infinite
done
clear
View Answer play_arrow
question_answer 10) The unit of thermal conductance is
A)
\[W{{K}^{-1}}\]
done
clear
B)
\[J{{K}^{-1}}\]
done
clear
C)
\[WK\]
done
clear
D)
\[JK\]
done
clear
View Answer play_arrow
question_answer 11) The value of P so that the vectors\[2i-j+k,\] \[i+2j-3k\]and\[3i+pj+5k\]are coplanar should be
A)
16
done
clear
B)
\[-4\]
done
clear
C)
4
done
clear
D)
\[-8\]
done
clear
View Answer play_arrow
question_answer 12) If the unit of force is 1 kN the length is 1 km and time 100 s, what will be the unit of mass?
A)
1000kg
done
clear
B)
1kg
done
clear
C)
10000kg
done
clear
D)
100kg
done
clear
View Answer play_arrow
question_answer 13) The maximum tension which an inextensible ring of mass 0.1 kg/m can bear is 10 N. The maximum velocity in m/s with which it can be rotated is
A)
10
done
clear
B)
\[\sqrt{10}\]
done
clear
C)
20
done
clear
D)
15
done
clear
View Answer play_arrow
question_answer 14) If there were a reduction in gravitational effect, which of the following forces do you think would change in some respect?
A)
Magnetic force
done
clear
B)
Electrostatic force
done
clear
C)
Viscous force
done
clear
D)
Archimedes uplift
done
clear
View Answer play_arrow
question_answer 15) The breaking force for a wire of diameter\[D\]of a material is F. The breaking force for a wire of the same material of radius D is
A)
F
done
clear
B)
2F
done
clear
C)
\[\frac{F}{4}\]
done
clear
D)
4F
done
clear
View Answer play_arrow
question_answer 16) The maximum range of a gun on horizontal terrain is 16 km if\[g=10\text{ }m/{{s}^{2}}\]. What must be the muzzle velocity of the shell?
A)
200 m/s
done
clear
B)
100 m/s
done
clear
C)
400 m/s
done
clear
D)
300 m/s
done
clear
View Answer play_arrow
question_answer 17) The length, breadth and thickness of a block are given by\[l=12\text{ }cm,\text{ }b=6\text{ }cm\]and\[t=2.45\]cm. The volume of the block according to the idea of significant figures should be
A)
\[1\times {{10}^{2}}c{{m}^{3}}\]
done
clear
B)
\[2\times {{10}^{2}}c{{m}^{3}}\]
done
clear
C)
\[1.763\times {{10}^{2}}c{{m}^{3}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 18) Five particles of mass 2 kg are attached to the rim of a circular disc of radius 0.1 m and negligible mass. Moment of inertia of the system about the axis passing through the centre of the disc and perpendicular to its plane is
A)
\[1\,kg\,{{m}^{2}}\]
done
clear
B)
\[0.1\,kg\,{{m}^{2}}\]
done
clear
C)
\[2\,kg\,{{m}^{2}}\]
done
clear
D)
\[0.2\,kg\,{{m}^{2}}\]
done
clear
View Answer play_arrow
question_answer 19) The radius of the convex surface of plan convex lens is 20 cm and the refractive index of the material of the lens is 1.5. The focal length is
A)
30 cm
done
clear
B)
50 cm
done
clear
C)
20 cm
done
clear
D)
40 cm
done
clear
View Answer play_arrow
question_answer 20) An ice-cube of density\[900\text{ }kg/{{m}^{3}}\]is floating in water of density\[1000\text{ }kg/{{m}^{3}}\]. The percentage of volume of ice-cube outside the water is
A)
20%
done
clear
B)
35%
done
clear
C)
10%
done
clear
D)
25%
done
clear
View Answer play_arrow
question_answer 21) A sphere of diameter 0.2 m and mass 2 kg is rolling on an inclined plane with velocity\[v=0.5\text{ }m/s\]. The kinetic energy of the sphere is
A)
0.1 J
done
clear
B)
0.3 J
done
clear
C)
0.5 J
done
clear
D)
0.42 J
done
clear
View Answer play_arrow
question_answer 22) An electron moves at right angle to a magnetic field of\[1.5\times {{10}^{-2}}\]tesia with a speed of\[6\times {{10}^{7}}\] m/s. If the specific charge of the electron is \[1.7\times {{10}^{11}}\] C/kg. The radius of the circular path will be
A)
2.9cm
done
clear
B)
3.9cm
done
clear
C)
2.35cm
done
clear
D)
2cm
done
clear
View Answer play_arrow
question_answer 23) If work function of a metal is 4.2 eV, the cut off wavelength is
A)
\[8000\text{ }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
B)
\[7000\text{ }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
C)
\[\text{1472 }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
D)
\[\text{2950 }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 24) A particle is executing the motion\[x=a\cos (\omega t-\theta )\]. The velocity of the particle is
A)
\[a\omega \,\cos \theta \]
done
clear
B)
\[a\omega \]
done
clear
C)
\[a\omega \,\sin \theta \]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 25) A particle is executing two different simple harmonic motions, mutually perpendicular, of different amplitudes and having phase difference of\[\frac{\pi }{2}\]. The path of the particle will be
A)
circular
done
clear
B)
straight line
done
clear
C)
parabolic
done
clear
D)
elliptical
done
clear
View Answer play_arrow
question_answer 26) Equations of motion in the same direction are given by \[{{y}_{1}}=2a\,\sin (\omega t-kx)\] \[{{y}_{2}}=2a\,\sin (\omega t-kx-\theta )\] The amplitude of the medium particle will be
A)
\[2a\,\cos \theta \]
done
clear
B)
\[\sqrt{2}a\,\cos \theta \]
done
clear
C)
\[4a\,\cos \frac{\theta }{2}\]
done
clear
D)
\[\sqrt{2}a\,\cos \frac{\theta }{2}\]
done
clear
View Answer play_arrow
question_answer 27) The work function of sodium is 2.3 eV. The threshold wavelength of sodium will be
A)
\[2900\text{ }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
B)
\[\text{2500 }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
C)
\[\text{5380 }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
D)
\[\text{1200 }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
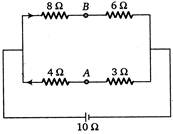
question_answer 28)
The potential difference between points A and B is
A)
\[\frac{20}{7}V\]
done
clear
B)
\[\frac{40}{7}V\]
done
clear
C)
\[\frac{10}{7}V\]
done
clear
D)
Zero
done
clear
View Answer play_arrow
question_answer 29) A short linear object of length b lies along the axis of a concave mirror of focal length\[f\]at a distance u from the pole of the mirror, what is the size of image?
A)
\[\left( \frac{f}{u-f} \right)b\]
done
clear
B)
\[{{\left( \frac{f}{u-f} \right)}^{2}}b\]
done
clear
C)
\[\left( \frac{f}{u-f} \right){{b}^{2}}\]
done
clear
D)
\[\left( \frac{f}{u-f} \right)\]
done
clear
View Answer play_arrow
question_answer 30) A closed argon pipe and an open argan pipe are tuned to the same fundamental frequency. What is the ratio of their lengths?
A)
\[1:2\]
done
clear
B)
\[2:1\]
done
clear
C)
\[2:3\]
done
clear
D)
\[4:3\]
done
clear
View Answer play_arrow
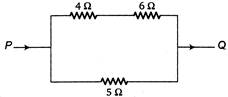
question_answer 31)
When a certain current is passed in the circuit as shown in figure, 10 kcal of heat is produced in\[5\,\Omega \]. resistance. How much heat is produced in\[4\,\Omega \]resistance?
A)
4 kcal
done
clear
B)
2 kcal
done
clear
C)
5 kcal
done
clear
D)
3 kcal
done
clear
View Answer play_arrow
question_answer 32) A steel scale measures the length of a copper wire as 80.0 cm, when both are at\[20{}^\circ C,\]the calibration temperature for the scale. What would the scale read for the length of the rod when both are at\[40{}^\circ C\]. Given: \[\alpha \]for steel\[=11\times {{10}^{-6}}per{}^\circ C\] and a for\[Cu=17\times {{10}^{-6}}per{}^\circ C\].
A)
80.0096cm
done
clear
B)
80.0272 cm
done
clear
C)
1cm
done
clear
D)
25.2cm
done
clear
View Answer play_arrow
question_answer 33) A tank is filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet?
A)
\[2\sqrt{h(H-h)}\]
done
clear
B)
\[4\sqrt{h(H+h)}\]
done
clear
C)
\[4\sqrt{h(H-h)}\]
done
clear
D)
\[2\sqrt{h(H+h)}\]
done
clear
View Answer play_arrow
question_answer 34) A raft of wood of mass 120 kg floats in water. The weight that can be put on the raft to make it just sink, should be \[{{d}_{raft}}=600\,kg/{{m}^{3}}\]
A)
80kg
done
clear
B)
50kg
done
clear
C)
60kg
done
clear
D)
30kg
done
clear
View Answer play_arrow
question_answer 35) A particle is kept at rest at the top of a sphere of diameter 42 m. When disturbed slightly, it slides down. At what height h from the bottom, the particle will leave the sphere
A)
14m
done
clear
B)
28m
done
clear
C)
35m
done
clear
D)
7m
done
clear
View Answer play_arrow
question_answer 36) If an insulated non-conducting sphere of radius R has charge density\[\rho \]. The electric field at a distance r from the centre of sphere\[(r>R)\]will be
A)
\[\frac{\rho R}{3{{\varepsilon }_{0}}}\]
done
clear
B)
\[\frac{\rho r}{{{\varepsilon }_{0}}}\]
done
clear
C)
\[\frac{\rho r}{3{{\varepsilon }_{0}}}\]
done
clear
D)
\[\frac{3\rho R}{{{\varepsilon }_{0}}}\]
done
clear
View Answer play_arrow
question_answer 37) The minimum wavelength of X-rays emitted by X-rays tube is\[0.4125\text{ }\overset{o}{\mathop{\text{A}}}\,\]. The accelerating voltage is
A)
30 kV
done
clear
B)
50 kV
done
clear
C)
80 kV
done
clear
D)
60 kV
done
clear
View Answer play_arrow
question_answer 38) A monoatomic gas supplied the heat Q very slowly keeping the pressure constant. The work done by the gas will be
A)
\[\frac{2}{3}Q\]
done
clear
B)
\[\frac{3}{5}Q\]
done
clear
C)
\[\frac{2}{5}Q\]
done
clear
D)
\[\frac{1}{5}Q\]
done
clear
View Answer play_arrow
question_answer 39)
The refractive index of the material of the prism and liquid are 1.56 and 1.32 respectively. What will be the value of 9 for the following refraction?
A)
\[\sin \theta \ge \frac{13}{11}\]
done
clear
B)
\[\sin \theta \ge \frac{11}{13}\]
done
clear
C)
\[\sin \theta \ge \frac{3}{12}\]
done
clear
D)
\[\sin \theta \ge \frac{1}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 40) The temperature of the black body increases from T to 2T. The factor by which the rate of emission will increase, is?
A)
4
done
clear
B)
2
done
clear
C)
16
done
clear
D)
8
done
clear
View Answer play_arrow
question_answer 41) A police jeep is chasing with velocity of 45 km/h a thief in another jeep moving with velocity 153 km/h. Police fires a bullet with muzzle velocity of 180 m/s. The velocity it will strike the car of the thief is
A)
150 m/s
done
clear
B)
27 m/s
done
clear
C)
450 m/s
done
clear
D)
250 m/s
done
clear
View Answer play_arrow
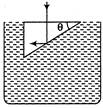
question_answer 42)
What should be the minimum value of refractive index of the material of the prism for the reflections to take place as shown in the figure
A)
1.7
done
clear
B)
1.4
done
clear
C)
1.2
done
clear
D)
2.7
done
clear
View Answer play_arrow
question_answer 43) An L-C circuit is in the state of resonance. If \[C=0.1\text{ }\mu F\]and\[L=0.25\text{ }H\]. Neglecting ohmic resistance of circuit. What is the frequency of oscillations?
A)
1007 Hz
done
clear
B)
100 Hz
done
clear
C)
109 Hz
done
clear
D)
500 Hz
done
clear
View Answer play_arrow
question_answer 44) A person who can see things most clearly at a distance of 10 cm, requires spectacles to enable to see clearly things at a distance of 30 cm. What should be the focal length of the spectacles?
A)
15 cm (concave)
done
clear
B)
15 cm (convex)
done
clear
C)
10 cm
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 45) The dimensional formula for Youngs modulus is
A)
\[[M{{L}^{-1}}{{T}^{-2}}]\]
done
clear
B)
\[[{{M}^{0}}L{{T}^{-2}}]\]
done
clear
C)
\[[ML{{T}^{-2}}]\]
done
clear
D)
\[[M{{L}^{2}}{{T}^{-2}}]\]
done
clear
View Answer play_arrow
question_answer 46) When temperature of an ideal gas is increased from\[27{}^\circ C\]to\[227{}^\circ C,\]its rms speed is changed from 400 m/s to\[{{v}_{s}}\]. The\[{{v}_{s}}\] is
A)
516 m/s
done
clear
B)
45 m/s
done
clear
C)
310 m/s
done
clear
D)
746 m/s
done
clear
View Answer play_arrow
question_answer 47) A simple pendulum of length I has a maximum angular displacement 6. The maximum kinetic energy of the bob is
A)
\[mgl\text{ }(1-cos\text{ }\theta \text{)}\]
done
clear
B)
\[0.5\text{ }mgl\]
done
clear
C)
\[mgl\]
done
clear
D)
\[0.5\text{ }mgl\]
done
clear
View Answer play_arrow
question_answer 48) Radius of orbit of satellite of earth is R. Its kinetic energy is proportional to
A)
\[\frac{1}{R}\]
done
clear
B)
\[\frac{1}{\sqrt{R}}\]
done
clear
C)
\[R\]
done
clear
D)
\[\frac{1}{{{R}^{3/2}}}\]
done
clear
View Answer play_arrow
question_answer 49) The radius R of the soap bubble is doubled under isothermal condition. If T be the surface tension of soap bubble. The work done in doing so is given by
A)
\[32\pi {{R}^{2}}T\]
done
clear
B)
\[24\pi {{R}^{2}}T\]
done
clear
C)
\[8\pi {{R}^{2}}T\]
done
clear
D)
\[4\pi {{R}^{2}}T\]
done
clear
View Answer play_arrow
question_answer 50) A body of specific heat\[0.2\text{ }kcal/kg{}^\circ C\]is heated through\[100{}^\circ C\].The percentage increase in its mass is
A)
9%
done
clear
B)
\[9.3\times {{10}^{-11}}%\]
done
clear
C)
10%
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 51) Two similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field through both coils, if the same current is flown
A)
\[1:\sqrt{2}\]
done
clear
B)
\[1:2\]
done
clear
C)
\[1:2\]
done
clear
D)
\[\sqrt{3}:1\]
done
clear
View Answer play_arrow
question_answer 52) A prism of refractive index\[\sqrt{2}\]has a refracting angle of\[60{}^\circ \]. At what angle a ray must be. incident on it so that it suffers a minimum deviation
A)
\[45{}^\circ \]
done
clear
B)
\[60{}^\circ \]
done
clear
C)
\[90{}^\circ \]
done
clear
D)
\[180{}^\circ \]
done
clear
View Answer play_arrow
question_answer 53) A cone filled with water is revolved in a vertical circle of radius 4 m and the water does not fall down. What must be the maximum period of revolution?
A)
2s
done
clear
B)
4s
done
clear
C)
1s
done
clear
D)
6s
done
clear
View Answer play_arrow
question_answer 54) A conducting sphere of radius R = 20 cm is given a charge\[Q=16\mu C\]. What is E at centre?
A)
\[3.6\times {{10}^{6}}N/C\]
done
clear
B)
\[1.8\times {{10}^{6}}N/C\]
done
clear
C)
Zero
done
clear
D)
\[0.9\times {{10}^{6}}N/C\]
done
clear
View Answer play_arrow
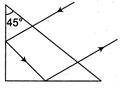
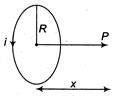
question_answer 55)
A coil having N turns carry a current as shown in the figure. The magnetic field intensity at point P is
A)
\[\frac{{{\mu }_{0}}Ni{{R}^{2}}}{2{{({{R}^{2}}+{{x}^{2}})}^{3/2}}}\]
done
clear
B)
\[\frac{{{\mu }_{0}}Ni}{2\pi R}\]
done
clear
C)
\[\frac{{{\mu }_{0}}Ni{{R}^{2}}}{{{(R+x)}^{2}}}\]
done
clear
D)
Zero
done
clear
View Answer play_arrow
question_answer 56) When glycerol is heated with\[KHS{{O}_{4}},\]it gives
A)
\[C{{H}_{2}}=CH-C{{H}_{3}}\]
done
clear
B)
\[C{{H}_{2}}=CH-C{{H}_{2}}OH\]
done
clear
C)
\[C{{H}_{2}}=CH-CHO\]
done
clear
D)
\[C{{H}_{2}}=C=C{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 57) Nitrous oxide is
A)
acidic
done
clear
B)
basic
done
clear
C)
amphoteric
done
clear
D)
neutral
done
clear
View Answer play_arrow
question_answer 58) For the redox reaction\[MnO_{4}^{-}+{{C}_{2}}O_{4}^{2-}+{{H}^{+}}\xrightarrow[{}]{{}}M{{n}^{2+}}+C{{O}_{2}}\]\[+{{H}_{2}}O\]the correct coefficients for the balanced reaction are
A)
\[MnO_{4}^{-}\] \[{{C}_{2}}O_{4}^{2-}\] \[{{H}^{+}}\] 2 5 16
done
clear
B)
\[MnO_{4}^{-}\] \[{{C}_{2}}O_{4}^{2-}\] \[{{H}^{+}}\] 16 5 2
done
clear
C)
\[MnO_{4}^{-}\] \[{{C}_{2}}O_{4}^{2-}\] \[{{H}^{+}}\] 5 16 2
done
clear
D)
\[MnO_{4}^{-}\] \[{{C}_{2}}O_{4}^{2-}\] \[{{H}^{+}}\] 2 16 5
done
clear
View Answer play_arrow
question_answer 59) To dissolve 0.9 g metal, 100 mL of\[1\text{ }N\text{ }HCl\]is used. What is the equivalent weight of metal?
A)
7
done
clear
B)
9
done
clear
C)
10
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 60) The thermal decomposition of a molecule shows first order kinetics. The molecule decomposes 50% in 120 min. How much time it will take to decompose 90%?
A)
300 min
done
clear
B)
360 min
done
clear
C)
398.8mm
done
clear
D)
400 min
done
clear
View Answer play_arrow
question_answer 61) Which equation is correct for adiabatic process?
A)
\[Q=+W\]
done
clear
B)
\[\Delta Q=0\]
done
clear
C)
\[\Delta E=Q\]
done
clear
D)
\[p+\Delta V=0\]
done
clear
View Answer play_arrow
question_answer 62) What is the product of the reaction\[{{C}_{6}}{{H}_{5}}COOC{{H}_{3}}\xrightarrow[{}]{LiAl{{H}_{4}}}...+...?\]
A)
\[{{C}_{6}}{{H}_{5}}COOH+C{{H}_{3}}OH\]
done
clear
B)
\[{{C}_{6}}{{H}_{5}}C{{H}_{2}}OH+C{{H}_{3}}OH\]
done
clear
C)
\[{{C}_{6}}{{H}_{5}}CHO+C{{H}_{3}}COOH\]
done
clear
D)
All of the above products
done
clear
View Answer play_arrow
question_answer 63) The example of Friedel-Crafts reaction is
A)
\[{{C}_{6}}{{H}_{6}}+{{C}_{2}}{{H}_{5}}Cl\xrightarrow[{}]{AlC{{l}_{3}}}{{C}_{6}}{{H}_{5}}{{C}_{2}}{{H}_{5}}\]\[+HCl\]
done
clear
B)
\[{{C}_{2}}{{H}_{5}}OH+HCl\xrightarrow[{}]{ZnC{{l}_{2}}}{{C}_{2}}{{H}_{5}}Cl+{{H}_{2}}O\]
done
clear
C)
\[{{C}_{6}}{{H}_{5}}Cl+C{{H}_{3}}COCl\xrightarrow[{}]{AlC{{l}_{3}}}{{C}_{6}}{{H}_{5}}COC{{H}_{3}}\]\[+C{{l}_{2}}\]
done
clear
D)
\[{{C}_{6}}{{H}_{5}}Br+Mg\xrightarrow[{}]{Ether}{{C}_{2}}{{H}_{5}}MgBr\]
done
clear
View Answer play_arrow
question_answer 64) The night-blindness is developed due to shortage of which vitamin?
A)
Vitamin \[{{B}_{6}}\]
done
clear
B)
Vitamin C
done
clear
C)
Vitamin \[{{B}_{12}}\]
done
clear
D)
Vitamin A
done
clear
View Answer play_arrow
question_answer 65) Which one of the following forms propane nitrile as the major product?
A)
Ethyl bromide\[+\]alcoholic\[KCN\]
done
clear
B)
Propyl bromide\[+\]alcoholic\[KCN\]
done
clear
C)
Propyl bromide\[+\]alcoholic\[AgCN\]
done
clear
D)
Ethyl bromide\[+\]alcoholic\[AgCN\]
done
clear
View Answer play_arrow
question_answer 66) \[1\text{ }d{{m}^{3}}\]solution containing\[{{10}^{-5}}\]moles each of \[C{{l}^{-}}\]ions and\[CrO_{4}^{2-}\]ions is treated with\[{{10}^{-4}}\] moles of silver nitrate. Which one of the following observations is made? \[[{{K}_{sp}}A{{g}_{2}}Cr{{O}_{4}}=4\times {{10}^{-12}}]\] \[[{{K}_{sp}}AgCl=1\times {{10}^{-10}}]\]
A)
Precipitation does not occur
done
clear
B)
Silver chromate gets precipitated first
done
clear
C)
Silver chloride gets precipitated first
done
clear
D)
Both silver chromate and silver chloride start precipitating simultaneously
done
clear
View Answer play_arrow
question_answer 67) A white crystalline salt A reacts with dilute\[HCl\]to liberate a suffocating gas B and also forms a yellow precipitate. The gas B turns potassium dichromate acidified with dilute \[{{H}_{2}}S{{O}_{4}}\]to a green coloured solution C. A, B and C are respectively
A)
\[N{{a}_{2}}S{{O}_{3}},S{{O}_{2}},C{{r}_{2}}{{(S{{O}_{4}})}_{3}}\]
done
clear
B)
\[N{{a}_{2}}{{S}_{2}}{{O}_{3}},S{{O}_{2}},C{{r}_{2}}{{(S{{O}_{4}})}_{3}}\]
done
clear
C)
\[N{{a}_{2}}{{S}_{2}}{{O}_{3}},C{{r}_{2}}{{(S{{O}_{4}})}_{3}}\]
done
clear
D)
\[N{{a}_{2}}S{{O}_{4}},S{{O}_{2}},C{{r}_{2}}{{(S{{O}_{4}})}_{3}}\]
done
clear
View Answer play_arrow
question_answer 68) Which one of the following statements is true?
A)
Saponification of oil yields a dial
done
clear
B)
Drying of oil involves hydrolysis
done
clear
C)
Addition of antioxidant to oil minimizes rancidity
done
clear
D)
Refining of oil involves hydrogenation
done
clear
View Answer play_arrow
question_answer 69) 9.65 C of electric current is passed through fused anhydrous magnesium chloride. The magnesium metal thus, obtained is completely converted into a Grignard reagent. The number of moles of the Grignard reagent obtained is
A)
\[5\times {{10}^{-4}}\]
done
clear
B)
\[1\times {{10}^{-4}}\]
done
clear
C)
\[5\times {{10}^{-5}}\]
done
clear
D)
\[1\times {{10}^{-5}}\]
done
clear
View Answer play_arrow
question_answer 70) The letter\[D\]in D-glucose signifies
A)
configuration at all chiral carbons
done
clear
B)
dextrorotatory
done
clear
C)
that it is a monosaccharide
done
clear
D)
configuration at a particular chiral carbon
done
clear
View Answer play_arrow
question_answer 71) Chloroacetic acid is a stronger acid than acetic acid. This can be explained using
A)
\[-M\] effect
done
clear
B)
\[-I\]effect
done
clear
C)
\[+M\]effect
done
clear
D)
\[+I\]effect
done
clear
View Answer play_arrow
question_answer 72) Time required for 100 per cent completion of a zero order reaction is
A)
\[\frac{2k}{a}\]
done
clear
B)
\[\frac{a}{2k}\]
done
clear
C)
\[\frac{a}{k}\]
done
clear
D)
\[ak\]
done
clear
View Answer play_arrow
question_answer 73) One mole of an organic compound A with the formula\[{{C}_{3}}{{H}_{8}}O\]reacts completely with two moles of\[HI\]to form \[X\] and Y. When Y is boiled with aqueous alkali, it forms Z. Z answers the iodo form test. The compound A is
A)
propan-2-ol
done
clear
B)
propan-1-ol
done
clear
C)
ethoxyethane
done
clear
D)
methoxyethane
done
clear
View Answer play_arrow
question_answer 74) 1 g of silver gets distributed between\[10\text{ }c{{m}^{3}}\]of molten zinc and\[100\text{ }c{{m}^{3}}\]of molten lead at\[800{}^\circ C\]. The distribution constant is 300. The percentage of silver in the zinc layer is approximately
A)
89
done
clear
B)
91
done
clear
C)
97
done
clear
D)
94
done
clear
View Answer play_arrow
question_answer 75) In which one of the following, does the given amount of chlorine exert the least pressure in a vessel of capacity\[1\text{ }d{{m}^{3}}\]at 273 K?
A)
0.0355 g
done
clear
B)
0.071 g
done
clear
C)
\[6.023\times {{10}^{21}}\]molecules
done
clear
D)
0.02 mol
done
clear
View Answer play_arrow
question_answer 76) For one mole of an ideal gas, increasing the temperature from\[10{}^\circ C\]to\[20{}^\circ C\]
A)
increases the average kinetic energy by two times
done
clear
B)
increases the rms velocity by\[\sqrt{2}\]times
done
clear
C)
increases the rms velocity by two times
done
clear
D)
increases both the average kinetic energy and rms velocity, but not significantly
done
clear
View Answer play_arrow
question_answer 77) Enthalpy of vaporization of benzene is\[+35.3kJ\] \[mo{{l}^{-1}}\]at its boiling point,\[80{}^\circ C\]. The entropy change in the transition of the vapour to liquid at its boiling point [in\[J{{K}^{-1}}mo{{l}^{-1}}\]]is
A)
\[-\,441\]
done
clear
B)
\[-100\]
done
clear
C)
\[+441\]
done
clear
D)
\[+100\]
done
clear
View Answer play_arrow
question_answer 78) The correct order of boiling points of the hydrides of nitrogen family is
A)
\[N{{H}_{3}}>P{{H}_{3}}>As{{H}_{3}}>Sb{{H}_{3}}\]
done
clear
B)
\[P{{H}_{3}}<As{{H}_{3}}<N{{H}_{3}}<Sb{{H}_{3}}\]
done
clear
C)
\[N{{H}_{3}}<P{{H}_{3}}<Sb{{H}_{3}}<As{{H}_{3}}\]
done
clear
D)
\[N{{H}_{3}}<P{{H}_{3}}<As{{H}_{3}}<Sb{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 79)
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 80) \[Ca{{C}_{2}}+{{N}_{2}}\xrightarrow[{}]{{}}X\]What is the X?
A)
\[CaCN\]
done
clear
B)
\[Ca{{(CN)}_{2}}\]
done
clear
C)
\[CaC{{N}_{2}}\]
done
clear
D)
\[Ca{{C}_{2}}{{N}_{2}}\]
done
clear
View Answer play_arrow
question_answer 81) Which of the following acts as an oxidizing agent?
A)
\[HN{{O}_{3}}\]
done
clear
B)
\[C{{l}_{2}}\]
done
clear
C)
\[FeC{{l}_{3}}\]
done
clear
D)
All of these
done
clear
View Answer play_arrow
question_answer 82) The shape of\[CI{{F}_{3}}\]is
A)
distorted T-shape
done
clear
B)
pyramidal
done
clear
C)
tetrahedral
done
clear
D)
trigonal planar
done
clear
View Answer play_arrow
question_answer 83) The\[{{t}_{1/2}}\]of first order reaction is
A)
dependent of initial concentration
done
clear
B)
directly proportional to initial concentration
done
clear
C)
indirectly proportional to initial concentration
done
clear
D)
independent of initial concentration
done
clear
View Answer play_arrow
question_answer 84) The\[{{K}_{sp}}\]of\[C{{a}_{3}}{{(P{{O}_{4}})}_{2}}\]is
A)
\[[C{{a}^{2+}}]{{[PO_{4}^{3-}]}^{2}}\]
done
clear
B)
\[{{[C{{a}^{2+}}]}^{3}}[PO_{4}^{3-}]\]
done
clear
C)
\[[C{{a}^{2+}}][PO_{4}^{3-}]\]
done
clear
D)
\[{{[C{{a}^{2+}}]}^{3}}{{[PO_{4}^{3-}]}^{2}}\]
done
clear
View Answer play_arrow
question_answer 85) The oxidation number of platinum in\[[Pt{{(N{{H}_{3}})}_{5}}Cl]C{{l}_{3}}\]is
A)
2
done
clear
B)
3
done
clear
C)
4
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 86) If\[\Delta G=46.06\text{ }kcal/mol,\]\[{{K}_{p}}\]at 300 K is
A)
\[{{10}^{-33.33}}\]
done
clear
B)
\[{{10}^{-23.03}}\]
done
clear
C)
\[{{10}^{-50.12}}\]
done
clear
D)
\[{{10}^{+33.33}}\]
done
clear
View Answer play_arrow
question_answer 87) \[{{N}_{2}}O\]is isoelectronic to\[C{{O}_{2}}\]and\[N_{3}^{-}\]. Which of the following is the structure of\[{{N}_{2}}O\]?
A)
done
clear
B)
\[N-O-N\]
done
clear
C)
\[N-N-O\]
done
clear
D)
done
clear
View Answer play_arrow
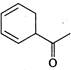
question_answer 88)
The IUPAC name of
A)
1-cyclohexa-2, 4-dienylethanone
done
clear
B)
3-cyclohexa-2, 4-dienylethanone
done
clear
C)
1-cyclohexa-3, 5-dienylethanone
done
clear
D)
3-cyclohexa-3, 5-dienylethanone
done
clear
View Answer play_arrow
question_answer 89) The IUPAC name of compound\[{{K}_{3}}[Fe{{(CN)}_{5}}NO]\]is
A)
pentacyano nitrosyi potassium ferrate (II)
done
clear
B)
potassium cyano pentanitrosyi ferrate (II)
done
clear
C)
potassium pentacyanonitrosyi ferrate (III)
done
clear
D)
potassium pentacyanonitrosyi ferrate (II)
done
clear
View Answer play_arrow
question_answer 90) 3-pentanol on reaction with aluminium tertiary butoxide in the presence of acetone gives
A)
3-pentanal
done
clear
B)
2-pehtanal
done
clear
C)
3-pentanohe
done
clear
D)
2-pentanone
done
clear
View Answer play_arrow
question_answer 91)
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 92) The product formed in the reaction n-hexanamide\[+B{{r}_{2}}+KOH,\]is
A)
hexanamine
done
clear
B)
propanamme
done
clear
C)
butanamine
done
clear
D)
pentanamme
done
clear
View Answer play_arrow
question_answer 93) \[X\xrightarrow[{}]{cone.\text{ }NaOH}Furoic\text{ }acid+Furyl\text{ }alcohol\]Compound X is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 94) In a chemical reaction catalyst
A)
decreases the energy of activation
done
clear
B)
increases the energy of activation
done
clear
C)
does not change energy of activation
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 95) \[N{{a}_{2}}S+N{{a}_{2}}[Fe{{(CN)}_{5}}NO]\xrightarrow[{}]{{}}\]purple colour. It is due to
A)
\[N{{a}_{4}}[Fe{{(CN)}_{3}}NOS]\]
done
clear
B)
\[N{{a}_{3}}[Fe{{(CN)}_{5}}NOS]\]
done
clear
C)
\[N{{a}_{4}}[Fe{{(CN)}_{5}}NO]\]
done
clear
D)
\[N{{a}_{4}}[Fe{{(CN)}_{5}}NOS]\]
done
clear
View Answer play_arrow
question_answer 96) Silver chloride dissolves in aqueous ammonia due to the formation of
A)
\[{{[Ag{{(N{{H}_{3}})}_{2}}]}^{+}}\]
done
clear
B)
\[[Ag{{(N{{H}_{3}})}_{2}}]\]
done
clear
C)
\[{{[Ag{{(N{{H}_{4}})}_{2}}]}^{+}}\]
done
clear
D)
\[[Ag{{(N{{H}_{4}})}_{2}}]\]
done
clear
View Answer play_arrow
question_answer 97) Which of the following is most basic oxide?
A)
\[FeO\]
done
clear
B)
\[{{K}_{2}}O\]
done
clear
C)
\[Sn{{O}_{2}}\]
done
clear
D)
\[CuO\]
done
clear
View Answer play_arrow
question_answer 98) Degree of hydrolysis (to of a salt of weak acid and a strong base is given by
A)
\[h=\sqrt{{{K}_{h}}}\]
done
clear
B)
\[h=\sqrt{\frac{C}{{{K}_{h}}}}\]
done
clear
C)
\[h=\sqrt{\frac{{{K}_{h}}}{C}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 99) Hexachloroethane is also called
A)
artificial sweeter
done
clear
B)
artificial camphor
done
clear
C)
artificial polymer
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 100) The magnetic moment of\[[Co{{(N{{H}_{3}})}_{6}}]C{{l}_{3}}\]is
A)
1.73
done
clear
B)
2.83
done
clear
C)
6.6
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 101) Hybridisation, shape and magnetic moment of \[{{[Ni{{(CN)}_{4}}]}^{2-}}\]ion
A)
\[ds{{p}^{2}},\]square planar, zero
done
clear
B)
\[ds{{p}^{2}},\]square planar, 1.73
done
clear
C)
\[s{{p}^{3}}{{d}^{2}},\]octahedral, zero
done
clear
D)
\[{{d}^{2}}s{{p}^{3}},\]octahedral, 1.73
done
clear
View Answer play_arrow
question_answer 102) If\[\Delta H=-\text{ }25kcal,\text{ }T=300\text{ }K\]and\[\Delta S=9\text{ }cal,\] then the reaction is
A)
spontaneous
done
clear
B)
non-spontaneous
done
clear
C)
equilibrium state
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 103) \[NaN{{H}_{2}}+{{N}_{2}}O\xrightarrow[{}]{{}}X+NaOH+N{{H}_{3}}\].What is the X?
A)
\[Na{{N}_{2}}\]
done
clear
B)
\[N{{a}_{3}}N\]
done
clear
C)
\[Na{{N}_{3}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 104) The amount of heat measured for a reaction in bomb calorimeter is
A)
\[\Delta G\]
done
clear
B)
\[\Delta H\]
done
clear
C)
\[\Delta E\]
done
clear
D)
\[p.\Delta V\]
done
clear
View Answer play_arrow
question_answer 105) Which one is a colligative property?
A)
Boiling point
done
clear
B)
Vapour pressure
done
clear
C)
Osmotic pressure
done
clear
D)
Freezing point
done
clear
View Answer play_arrow
question_answer 106) Which one of the following statements is incorrect about the molecularity of a reaction?
A)
Molecularity of a reaction is the number of molecules of the reactants present in the balanced equation
done
clear
B)
Molecularity of a reaction is the number of molecules in the slowest step
done
clear
C)
Molecularity is always a whole number
done
clear
D)
There is no difference between order and molecularity of a reaction
done
clear
View Answer play_arrow
question_answer 107) The kinetic theory of gases predicts that total kinetic energy of a gaseous assembly depends on
A)
pressure of the gas
done
clear
B)
temperature of the gas
done
clear
C)
volume of the gas
done
clear
D)
pressure, volume and temperature of the gas
done
clear
View Answer play_arrow
question_answer 108) Phenol dimerises in benzene having vant Hoff factor 0.54. What is the degree of association?
A)
1.92
done
clear
B)
0.98
done
clear
C)
1.08
done
clear
D)
0.92
done
clear
View Answer play_arrow
question_answer 109) 3 g of an oxide of a metal is converted to chloride completely and it yielded 5 g of chloride. The equivalent weight of the metal is
A)
33.25
done
clear
B)
3.325
done
clear
C)
12
done
clear
D)
20
done
clear
View Answer play_arrow
question_answer 110) The reaction\[2{{N}_{2}}{{O}_{5}}2{{N}_{2}}{{O}_{4}}+{{O}_{2}}\] is
A)
bimolecular and second order
done
clear
B)
unimolecular and first order
done
clear
C)
bimolecular and first order
done
clear
D)
bimolecular and zero order
done
clear
View Answer play_arrow
question_answer 111) If X and V are independent variables, then correlation coefficient is
A)
1
done
clear
B)
\[-1\]
done
clear
C)
1/2
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 112) Let n persons sit on a round table. The odd against two specified persons sitting together is
A)
\[2:(n-3)\]
done
clear
B)
\[(n-1):2\]
done
clear
C)
\[(n-2):2\]
done
clear
D)
\[(n-3):2\]
done
clear
View Answer play_arrow
question_answer 113) If the roots of the equation\[\frac{{{x}^{2}}-bx}{ax-c}=\frac{m-1}{m+1}\]are equal and of opposite sign, then the value of m will be
A)
\[\frac{a-b}{a+b}\]
done
clear
B)
\[\frac{b-a}{a+b}\]
done
clear
C)
\[\frac{a+b}{a-b}\]
done
clear
D)
\[\frac{b+a}{b-a}\]
done
clear
View Answer play_arrow
question_answer 114) If \[\tan x=\frac{b}{a},\]then\[\sqrt{\frac{a+b}{a-b}}+\sqrt{\frac{a-b}{a+b}}\]is equal to
A)
\[\frac{2\sin x}{\sqrt{\sin 2x}}\]
done
clear
B)
\[\frac{2\cos x}{\sqrt{\cos 2x}}\]
done
clear
C)
\[\frac{2\cos x}{\sqrt{\sin 2x}}\]
done
clear
D)
\[\frac{2\sin x}{\sqrt{\cos 2x}}\]
done
clear
View Answer play_arrow
question_answer 115) If the lines of regression of Y on X and X on Y make angles\[30{}^\circ \]and\[60{}^\circ ,\]respectively with the positive direction of x-axis, then the correlation coefficient between X and Y is
A)
\[\frac{1}{\sqrt{2}}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[1\]
done
clear
D)
\[\frac{1}{3}\]
done
clear
View Answer play_arrow
question_answer 116) The distance of the point\[(-1,-5,-10)\]from the point of intersection of line \[\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{12}\]and plane\[x-y+z=5\]is
A)
10
done
clear
B)
8
done
clear
C)
21
done
clear
D)
13
done
clear
View Answer play_arrow
question_answer 117) Iz\[\sqrt{3}\cos \theta +\sin \theta =\sqrt{2},\]then general value of\[\theta \]is
A)
\[n\pi +{{(-1)}^{n}}\frac{\pi }{4}\]
done
clear
B)
\[{{(-1)}^{n}}\frac{\pi }{4}-\frac{\pi }{3}\]
done
clear
C)
\[n\pi +\frac{\pi }{4}-\frac{\pi }{3}\]
done
clear
D)
\[n\pi +{{(-1)}^{n}}\frac{\pi }{4}-\frac{\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 118) If for all values of x and y,\[f(x+y)=f(x)f(y)\]and\[f(5)=2,f(0)=3,\]then\[f(5)\]is
A)
3
done
clear
B)
4
done
clear
C)
5
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 119) If\[y=x-{{x}^{2}}+{{x}^{3}}-{{x}^{4}}+.....\infty ,\]then the value of \[x\]will be\[(-1<x<1)\]
A)
\[y+\frac{1}{y}\]
done
clear
B)
\[\frac{y}{1+y}\]
done
clear
C)
\[y-\frac{1}{y}\]
done
clear
D)
\[\frac{y}{1-y}\]
done
clear
View Answer play_arrow
question_answer 120) The number of vector of unit length perpendicular to plane of vector\[a=(1,1,0)\]and \[b=(0,1,1)\]is/are
A)
one
done
clear
B)
two
done
clear
C)
three
done
clear
D)
infinite
done
clear
View Answer play_arrow
question_answer 121) If \[\tan \frac{B-C}{2}=x\cos \frac{A}{2},\]then\[x\]is equal to
A)
\[\frac{c-a}{c+a}\]
done
clear
B)
\[\frac{a-b}{a+b}\]
done
clear
C)
\[\frac{b-c}{b+c}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 122) One root of the equation\[\left| \begin{matrix} x+a & b & c \\ b & x+c & a \\ c & a & x+b \\ \end{matrix} \right|=0\]is
A)
\[-(a+b)\]
done
clear
B)
\[-(b+c)\]
done
clear
C)
\[-a\]
done
clear
D)
\[-(a+b+c)\]
done
clear
View Answer play_arrow
question_answer 123) Let\[x\]and y be two variables and\[x>1,\text{ }xy=1,\] then minimum value of\[x+y\]is
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
\[3\frac{1}{3}\]
done
clear
View Answer play_arrow
question_answer 124) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin (\pi {{\cos }^{2}}x)}{{{x}^{2}}}\]equals to
A)
\[-\pi \]
done
clear
B)
\[\pi \]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[-\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 125) If the function,\[f(x)={{x}^{3}}-6{{x}^{2}}+ax+b\] satisfies Rolles theorem in the interval [1, 3] and\[f\left( \frac{2\sqrt{3}+1}{\sqrt{3}} \right)=0,\]then
A)
\[a=-11\]
done
clear
B)
\[a=-6\]
done
clear
C)
\[a=6\]
done
clear
D)
\[a=11\]
done
clear
View Answer play_arrow
question_answer 126) The solution of differential equation\[y-x\frac{dy}{dx}=a\left( {{y}^{2}}+\frac{dy}{dx} \right)\]is
A)
\[(x+a)(x+ay)=cy\]
done
clear
B)
\[(x+a)(1-ay)=cy\]
done
clear
C)
\[(x+a)(1-ay)=c\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 127) The maximum value of\[3\text{ }cos\text{ }\theta +4\text{ }sin\text{ }\theta \] is
A)
3
done
clear
B)
4
done
clear
C)
5
done
clear
D)
Nona of these
done
clear
View Answer play_arrow
question_answer 128) The domain of the function\[\sqrt{{{\log }_{e}}({{x}^{2}}-6x+6)}\]is
A)
\[(-\infty ,3-\sqrt{3}]\cup [3+\sqrt{3},\infty ]\]
done
clear
B)
\[(-\infty ,3-\sqrt{3}]\cup (3+\sqrt{3},\infty ]\]
done
clear
C)
\[(-\infty ,1]\cup [5,\infty )\]
done
clear
D)
\[(-\infty ,1)\cup (5,\infty )\]
done
clear
View Answer play_arrow
question_answer 129) \[\int{{{e}^{x}}(1-\cot x+{{\cot }^{2}}x)}\,dx\]equals to
A)
\[{{e}^{x}}\cot x+C\]
done
clear
B)
\[{{e}^{x}}\cos ecx+C\]
done
clear
C)
\[-{{e}^{x}}\cot x+C\]
done
clear
D)
\[-{{e}^{x}}\cos ecx+C\]
done
clear
View Answer play_arrow
question_answer 130) The speed v of a particle moving along a straight line is given by\[a+b{{v}^{2}}={{x}^{2}}\](where X, is its distance from the origin). The acceleration of the particle is
A)
\[bx\]
done
clear
B)
\[\frac{x}{a}\]
done
clear
C)
\[\frac{x}{b}\]
done
clear
D)
\[\frac{x}{ab}\]
done
clear
View Answer play_arrow
question_answer 131) If a and b are two different positive real numbers, then which of the following statements is true?
A)
\[2\sqrt{ab}>a+b\]
done
clear
B)
\[2\sqrt{ab}<a+b\]
done
clear
C)
\[2\sqrt{ab}=a+b\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 132) The area of the circle passes through the point (4, 6) and whose centre is (1, 2) is
A)
\[5\pi \] sq units
done
clear
B)
\[10\pi \]sq units
done
clear
C)
\[25\pi \] sq units
done
clear
D)
\[35\pi \]sq units
done
clear
View Answer play_arrow
question_answer 133) If\[\omega \]is a cube root of unity, then\[\left| \begin{matrix} 1 & \omega & {{\omega }^{2}} \\ \omega & {{\omega }^{2}} & 1 \\ {{\omega }^{2}} & 1 & \omega \\ \end{matrix} \right|\]is equal to
A)
1
done
clear
B)
0
done
clear
C)
\[\omega \]
done
clear
D)
\[{{\omega }^{2}}\]
done
clear
View Answer play_arrow
question_answer 134) Equation of circle passes through the points of intersection of circles\[{{x}^{2}}+{{y}^{2}}=6\]and \[{{x}^{2}}+{{y}^{2}}-6x+8=0\]and point (1, 1) is
A)
\[{{x}^{2}}+{{y}^{2}}-6x+4=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-3x+1=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-4y+2=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-6x-6y+10=0\]
done
clear
View Answer play_arrow
question_answer 135) Function\[f(x)=\cos x-2ax\]is monotonically decreasing when
A)
\[a<\frac{1}{2}\]
done
clear
B)
\[a>\frac{1}{2}\]
done
clear
C)
\[a<0\]
done
clear
D)
\[a>0\]
done
clear
View Answer play_arrow
question_answer 136) Equation of the ellipse with eccentricity - and foci at\[(\pm 1,\text{ }0)\]is
A)
\[\frac{{{x}^{2}}}{3}+\frac{{{y}^{2}}}{4}=1\]
done
clear
B)
\[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{3}=1\]
done
clear
C)
\[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{3}=\frac{4}{3}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 137) How many words can be formed the letters of the word COMMITTEE?
A)
\[\frac{9!}{{{(2!)}^{2}}}\]
done
clear
B)
\[\frac{9!}{{{(2!)}^{3}}}\]
done
clear
C)
\[\frac{9!}{2!}\]
done
clear
D)
\[9!\]
done
clear
View Answer play_arrow
question_answer 138) The integrating factor of linear differential equation \[\frac{dy}{dx}+y\tan x-\sec x=0\]
A)
\[cos\text{ }x\]
done
clear
B)
\[\sec \text{ }x\]
done
clear
C)
\[{{e}^{\cos x}}\]
done
clear
D)
\[{{e}^{\sin x}}\]
done
clear
View Answer play_arrow
question_answer 139) The value of \[\frac{2}{3!}+\frac{4}{5!}+\frac{6}{7!}+....\]is
A)
\[e\]
done
clear
B)
\[2e\]
done
clear
C)
\[{{e}^{2}}\]
done
clear
D)
\[2e\]
done
clear
View Answer play_arrow
question_answer 140) Let\[f(x)=\left\{ \begin{matrix} 0, & x<0 \\ {{x}^{2}}, & x\ge 0 \\ \end{matrix} \right.\]is
A)
\[f\]is continuous but not differentiable
done
clear
B)
\[f\]is differentiable but not continuous
done
clear
C)
\[f\]is continuous and differentiable
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 141) The lines\[3x-4y+4=0\]and\[6x-8y-7=0\]are tangents of the circle, then radius of the circle is
A)
\[\frac{1}{4}\]
done
clear
B)
\[\frac{3}{4}\]
done
clear
C)
\[\frac{5}{4}\]
done
clear
D)
\[2\]
done
clear
View Answer play_arrow
question_answer 142) Three vertices out of six vertices of a regular hexagon are chosen randomly. The probability of getting an equilateral triangle after joining three vertices is
A)
\[\frac{1}{5}\]
done
clear
B)
\[\frac{1}{20}\]
done
clear
C)
\[\frac{1}{10}\]
done
clear
D)
\[\frac{3}{20}\]
done
clear
View Answer play_arrow
question_answer 143) The equation of parabola whose focus is (5, 3) and directrix is\[3x-4y+1=0,\]is
A)
\[{{(4x+3y)}^{2}}-256x-142y+849=0\]
done
clear
B)
\[{{(4x-3y)}^{2}}-256x-142y+849=0\]
done
clear
C)
\[{{(3x+4y)}^{2}}-142x-256y+849=0\]
done
clear
D)
\[{{(3x-4y)}^{2}}-256x-142y+849=0\]
done
clear
View Answer play_arrow
question_answer 144) If\[f(x)=\frac{2-\sqrt{x+4}}{\sin 2x}(x\ne 0)\]is continuous function at\[x=0,\]then\[f(0)\]equals to
A)
\[\frac{1}{4}\]
done
clear
B)
\[-\frac{1}{4}\]
done
clear
C)
\[\frac{1}{8}\]
done
clear
D)
\[-\frac{1}{8}\]
done
clear
View Answer play_arrow
question_answer 145) Equation of the diameter of the circle \[{{x}^{2}}+{{y}^{2}}-6x+2y=0\]which passes through the origin is
A)
\[x+3y=0\]
done
clear
B)
\[x-3y=0\]
done
clear
C)
\[3x+y=0\]
done
clear
D)
\[3x-y=0\]
done
clear
View Answer play_arrow
question_answer 146) The equation of latusrectum of a parabola is \[x+y=8\]and the equation of the tangent at the vertex is\[x+y=12,\]then length of the latusrectum is
A)
\[4\sqrt{2}\]
done
clear
B)
\[2\sqrt{2}\]
done
clear
C)
8
done
clear
D)
\[8\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 147) The point z moves on the Argand diagram such that \[|z-3i|=2,\]then its locus is
A)
y-axis
done
clear
B)
a straight line
done
clear
C)
a circle
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 148) In a\[\Delta ABC,\]if\[a=2x,b=2y\]and\[\angle C=120{}^\circ ,\]then the area of the triangle is
A)
\[xy\]
done
clear
B)
\[xy\sqrt{3}\]
done
clear
C)
\[3xy\]
done
clear
D)
\[2xy\]
done
clear
View Answer play_arrow
question_answer 149) \[\int{\frac{dx}{\sin x-\cos x+\sqrt{2}}}\]is equal to
A)
\[\frac{1}{\sqrt{2}}\tan \left( \frac{x}{2}+\frac{\pi }{8} \right)+C\]
done
clear
B)
\[-\frac{1}{\sqrt{2}}\tan \left( \frac{x}{2}+\frac{\pi }{8} \right)+C\]
done
clear
C)
\[\frac{1}{\sqrt{2}}\cot \left( \frac{x}{2}+\frac{\pi }{8} \right)+C\]
done
clear
D)
\[-\frac{1}{\sqrt{2}}\cot \left( \frac{x}{2}+\frac{\pi }{8} \right)+C\]
done
clear
View Answer play_arrow
question_answer 150) The roots of the equation\[\left| \begin{matrix} 1 & 4 & 20 \\ 1 & -2 & 5 \\ 1 & 2x & 5{{x}^{2}} \\ \end{matrix} \right|=0\]are
A)
\[-1,-2\]
done
clear
B)
\[-1,2\]
done
clear
C)
\[1,-2\]
done
clear
D)
\[1,2\]
done
clear
View Answer play_arrow
question_answer 151) If the roots of the equation\[a{{x}^{2}}+bx+c=0\]are and\[2l,\]then
A)
\[{{b}^{2}}=9ac\]
done
clear
B)
\[2{{b}^{2}}=9ac\]
done
clear
C)
\[{{b}^{2}}=-4ac\]
done
clear
D)
\[{{a}^{2}}={{c}^{2}}\]
done
clear
View Answer play_arrow
question_answer 152) \[\frac{d}{dx}\left[ {{\sin }^{2}}{{\cot }^{-1}}\left\{ \sqrt{\frac{1-x}{1+x}} \right\} \right]\]equals to
A)
\[-1\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[-\frac{1}{2}\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 153) \[{{\sin }^{6}}\theta +{{\cos }^{6}}\theta +3{{\sin }^{2}}\theta {{\cos }^{2}}\theta \]is equal to
A)
0
done
clear
B)
\[-1\]
done
clear
C)
1
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 154) Let\[P(a\sec \theta ,b\tan \theta )\]and\[Q(a\sec \phi ,b\tan \phi ),\]where\[\theta +\phi =\frac{\pi }{2}\]be two points on the hyperbola\[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\]. If\[(h,k)\]is the point on intersection of the normals at P and Q, then k is equal to
A)
\[\frac{{{a}^{2}}+{{b}^{2}}}{a}\]
done
clear
B)
\[-\left( \frac{{{a}^{2}}+{{b}^{2}}}{a} \right)\]
done
clear
C)
\[\frac{{{a}^{2}}+{{b}^{2}}}{b}\]
done
clear
D)
\[-\left( \frac{{{a}^{2}}+{{b}^{2}}}{b} \right)\]
done
clear
View Answer play_arrow
question_answer 155) If\[\tan (A+B)=p,\tan (A-B)=q,\]then the value of tan 2A is
A)
\[\frac{p+q}{p-q}\]
done
clear
B)
\[\frac{p-q}{1+pq}\]
done
clear
C)
\[\frac{1+pq}{1-p}\]
done
clear
D)
\[\frac{p+q}{1-pq}\]
done
clear
View Answer play_arrow
question_answer 156) \[\int{\frac{dx}{\sqrt{{{e}^{2x}}-1}}}\]equals to
A)
\[{{\sin }^{-1}}({{e}^{x}})+C\]
done
clear
B)
\[{{\cos }^{-1}}({{e}^{x}})+C\]
done
clear
C)
\[{{\sec }^{-1}}({{e}^{x}})+C\]
done
clear
D)
\[{{\tan }^{-1}}({{e}^{x}})+C\]
done
clear
View Answer play_arrow
question_answer 157) If a curve\[y=a\sqrt{x}+bx\]passes through the point (1, 2) and the area bounded by the curve, line\[x=4\]and\[x-\]axis is 8 sq units, then
A)
\[a=3,b=-1\]
done
clear
B)
\[a=3,b=1\]
done
clear
C)
\[a=-3,b=1\]
done
clear
D)
\[a=-3,b=-1\]
done
clear
View Answer play_arrow
question_answer 158) The area of the region (in square unit) bounded by the curve\[{{x}^{2}}=4y,\]line\[x=2\]and\[x-\]axis is
A)
1
done
clear
B)
\[\frac{2}{3}\]
done
clear
C)
\[\frac{4}{3}\]
done
clear
D)
\[\frac{8}{3}\]
done
clear
View Answer play_arrow
question_answer 159) The order and degree of the differential equation representing the family of curves \[{{y}^{2}}=2k(x+\sqrt{k})\](where, k is positive parameter) are respectively,
A)
1 and 2
done
clear
B)
2 and 4
done
clear
C)
1 and 4
done
clear
D)
1 and 3
done
clear
View Answer play_arrow
question_answer 160) In a\[\Delta ABC,\text{ }a=2cm,\text{ }b=3cm\text{ }and\text{ }c=4cm,\]then\[\angle A\]is
A)
\[{{\cos }^{-1}}\left( \frac{1}{24} \right)\]
done
clear
B)
\[{{\cos }^{-1}}\left( \frac{11}{16} \right)\]
done
clear
C)
\[{{\cos }^{-1}}\left( \frac{7}{8} \right)\]
done
clear
D)
\[{{\cos }^{-1}}\left( -\frac{1}{4} \right)\]
done
clear
View Answer play_arrow
question_answer 161) The slope of the tangent at\[(x,y)\]to a curve passing through a point (2, 1) is\[\frac{{{x}^{2}}+{{y}^{2}}}{2xy}\],then the equation of the curve is
A)
\[2({{x}^{2}}-{{y}^{2}})=3x\]
done
clear
B)
\[2({{x}^{2}}-{{y}^{2}})=6y\]
done
clear
C)
\[x({{x}^{2}}-{{y}^{2}})=6\]
done
clear
D)
\[x({{x}^{2}}+{{y}^{2}})=10\]
done
clear
View Answer play_arrow
question_answer 162) If in the expansion of\[{{(1+x)}^{20}},\]the coefficients of rth and\[(r+4)\]th terms are equal, then value of r is
A)
7
done
clear
B)
8
done
clear
C)
9
done
clear
D)
10
done
clear
View Answer play_arrow
question_answer 163) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{{{\log }_{e}}(1+x)}{{{3}^{x}}-1}\]equals to
A)
\[{{\log }_{e}}3\]
done
clear
B)
0
done
clear
C)
1
done
clear
D)
\[{{\log }_{3}}e\]
done
clear
View Answer play_arrow
question_answer 164) If\[x=\exp \left\{ {{\tan }^{-1}}\left( \frac{y-{{x}^{2}}}{{{x}^{2}}} \right) \right\},\]then\[\frac{dy}{dx}\]equals to
A)
\[2x[1+\tan (\log x)]+2{{\sec }^{2}}(\log x)\]
done
clear
B)
\[x[1+\tan (\log x)]+{{\sec }^{2}}(\log x)\]
done
clear
C)
\[2x[1+\tan (\log x)]+{{x}^{2}}{{\sec }^{2}}(\log x)\]
done
clear
D)
\[2x[1+\tan (\log x)]+{{\sec }^{2}}(\log x)\]
done
clear
View Answer play_arrow
question_answer 165) If the roots of the equation\[5{{x}^{2}}-7x+k=0\]are reciprocal of each other, then value of k is
A)
5
done
clear
B)
2
done
clear
C)
2
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 166) The locus of a point whose difference of distance from points (3, 0) and\[(-3,0)\]is 4, is
A)
\[\frac{{{x}^{2}}}{4}-\frac{{{y}^{2}}}{5}=1\]
done
clear
B)
\[\frac{{{x}^{2}}}{5}-\frac{{{y}^{2}}}{4}=1\]
done
clear
C)
\[\frac{{{x}^{2}}}{2}-\frac{{{y}^{2}}}{3}=1\]
done
clear
D)
\[\frac{{{x}^{2}}}{3}-\frac{{{y}^{2}}}{2}=1\]
done
clear
View Answer play_arrow
question_answer 167) If the first term of an AP is 2 and common difference is 4, then sum of 40 terms is
A)
3200
done
clear
B)
1600
done
clear
C)
200
done
clear
D)
2800
done
clear
View Answer play_arrow
question_answer 168) The distance between the directories of a rectangular hyperbola is 10 units, then distance between its foci is
A)
\[10\sqrt{2}\]
done
clear
B)
\[5\]
done
clear
C)
\[5\sqrt{2}\]
done
clear
D)
\[20\]
done
clear
View Answer play_arrow
question_answer 169) \[{{C}_{1}}+2{{C}_{2}}+3{{C}_{3}}+...+n{{C}_{n}}\]is equal to
A)
\[{{2}^{n}}\]
done
clear
B)
\[n{{.2}^{n}}\]
done
clear
C)
\[n{{.2}^{n-1}}\]
done
clear
D)
\[n{{.2}^{n+1}}\]
done
clear
View Answer play_arrow
question_answer 170) If a particle is thrown vertically upwards with a velocity of u cm/s under gravity, then the time for the particle to come to earth again is
A)
\[\frac{u}{g}s\]
done
clear
B)
\[\frac{2u}{g}s\]
done
clear
C)
\[\frac{u}{2g}s\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
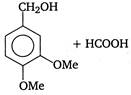
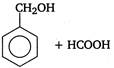
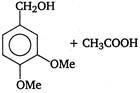
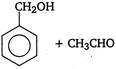
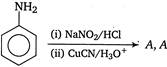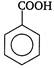
is
is
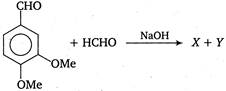Identify X and Y
