question_answer 1) Which of the following statements is wrong?
A)
Voltmeter should have high resistance
done
clear
B)
Ammeter should have low resistance
done
clear
C)
Ammeter is placed in parallel across the conductor in a circuit
done
clear
D)
Voltmeter is placed in parallel across the conductor in a circuit
done
clear
View Answer play_arrow
question_answer 2) As the temperature of hot junction increases the thermo emf
A)
always increases
done
clear
B)
always decreases
done
clear
C)
may increase or decrease
done
clear
D)
always remains constant
done
clear
View Answer play_arrow
question_answer 3) A proton and an \[\alpha \]-particle enter a uniform magnetic field perpendicularly with the same speed. If proton takes 25\[\mu F\] to make 5 revolutions, then the periodic time for the \[\alpha \]-particle would be
A)
50\[\mu s\]
done
clear
B)
25 \[\mu s\]
done
clear
C)
10 \[\mu s\]
done
clear
D)
5\[\mu s\]
done
clear
View Answer play_arrow
question_answer 4) Two parallel conductors A and B of equal length carry currents i and 10 i, respectively, in the same direction. Then
A)
A and B will repel each other with same force
done
clear
B)
A and B will attract each other with same force
done
clear
C)
A will attract B, but B will repel A
done
clear
D)
A and B will attract each other with different forces
done
clear
View Answer play_arrow
question_answer 5) An open pipe is suddenly closed at one end with the result that the frequency of third harmonic of the closed pipe is termed to be higher by 100 Hz than the fundamental frequency of the open pipe. The fundamental frequency of the open pipe is
A)
200 Hz
done
clear
B)
150 Hz
done
clear
C)
100 Hz
done
clear
D)
250 Hz
done
clear
View Answer play_arrow
question_answer 6) Two slits 4 mm apart, are illuminated by light of wavelength 6000\[\overset{0}{\mathop{A}}\,\]. What will be the fringe width on a screen placed 2 m from the slits?
A)
0.12 mm
done
clear
B)
0.3 mm
done
clear
C)
3.0 mm
done
clear
D)
4.0 mm
done
clear
View Answer play_arrow
question_answer 7) A thin prism \[{{P}_{1}}\] of angle \[4{}^\circ \] and refractive index \[1.54{}^\circ \] is combined with another thin prism \[{{P}_{2}}\] of refractive index 1.72 to produce dispersion without deviation. The angle of \[{{P}_{2}}\] is
A)
\[4{}^\circ \]
done
clear
B)
\[5.33{}^\circ \]
done
clear
C)
\[2.6{}^\circ \]
done
clear
D)
\[3{}^\circ \]
done
clear
View Answer play_arrow
question_answer 8) While viewing a distant object with a telescope suddenly a housefly sits on objective lens. The correct statement is that
A)
housefly will be seen enlarged in image
done
clear
B)
housefly will be seen reduced in image
done
clear
C)
intensity of image will be decreased
done
clear
D)
intensity of image will be increased
done
clear
View Answer play_arrow
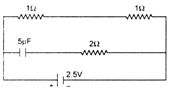
question_answer 9)
A capacitor of capacitance 5\[\mu F\] is connected as shown in the figure. The internal resistance of the cell is 0.5\[\Omega \] . The amount of charge on the capacitor plate is
A)
10 \[\Omega C\]
done
clear
B)
5\[\Omega C\]
done
clear
C)
6\[\Omega C\]
done
clear
D)
10.2 \[\Omega C\]
done
clear
View Answer play_arrow
question_answer 10) A charge of \[{{10}^{-9}}\] C is placed on each of the 64 identical drops of radius 2 cm. They are then combined to form a bigger drop. Its potential will be
A)
\[7.2\times {{10}^{3}}V\]
done
clear
B)
\[7.2\times {{10}^{2}}V\]
done
clear
C)
\[1.44\times {{10}^{2}}V\]
done
clear
D)
\[1.44\times {{10}^{3}}V\]
done
clear
View Answer play_arrow
question_answer 11) A particle moves in the xy-plane under the action of a force F such that the components of its linear momentum p at any time f are \[{{P}_{x}}=2\cos \,t,\,{{P}_{y}}=\sin \,t.\] The angle between F and p at time t is
A)
\[{{90}^{\text{o}}}\]
done
clear
B)
\[{{0}^{\text{o}}}\]
done
clear
C)
\[{{180}^{\text{o}}}\]
done
clear
D)
\[{{30}^{\text{o}}}\]
done
clear
View Answer play_arrow
question_answer 12) A fighter plane is moving in a vertical circle of radius r. Its minimum velocity at the highest point A of the circle will be
A)
\[\sqrt{3gr}\]
done
clear
B)
\[\sqrt{2gr}\]
done
clear
C)
\[\sqrt{gr}\]
done
clear
D)
\[\sqrt{gr/2}\]
done
clear
View Answer play_arrow
question_answer 13) In Millikans oil drop experiment, a charged drop of mass \[1.8\times {{10}^{-13}}\]kg is stationary between its plates. The distance between its plates is 0.9 cm and potential difference is 2000 V. The number of electrons in the drop is
A)
500
done
clear
B)
50
done
clear
C)
5
done
clear
D)
10
done
clear
View Answer play_arrow
question_answer 14) Decay constant of radium is \[\lambda \]. By a suitable process its compound radium bromide is obtained. The decay constant of radium bromide will be
A)
\[\lambda \]
done
clear
B)
more than \[\lambda \]
done
clear
C)
less than \[\lambda \]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 15) Rn decays into Po by emitting an \[\alpha \]-particle with half-life of 4 days. A sample contains \[6.4\times {{10}^{10}}\] atoms of Rn after 12 days, the number of atoms of Rn left in the sample will be
A)
\[3.2\times {{10}^{10}}\]
done
clear
B)
\[0.53\times {{10}^{10}}\]
done
clear
C)
\[2.1\times {{10}^{10}}\]
done
clear
D)
\[0.8\times {{10}^{10}}\]
done
clear
View Answer play_arrow
question_answer 16) The energy gap between the valence and conduction bands of an insulator is about
A)
0.1 eV
done
clear
B)
1.0 eV
done
clear
C)
5.0 eV
done
clear
D)
zero
done
clear
View Answer play_arrow
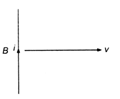
question_answer 17)
A conducting wire is moving towards right in a magnetic field B. The direction of induced current in the wire is shown in the figure. The direction of magnetic field will be
A)
in the plane of paper pointing towards right
done
clear
B)
in the plane of paper pointing towards left
done
clear
C)
perpendicular to the plane of paper and downwards
done
clear
D)
perpendicular to the plane of paper and upwards
done
clear
View Answer play_arrow
question_answer 18) An electron moving with velocity \[2\times {{10}^{-7}}\]m/s, describes a circle in a magnetic field of strength \[2\times {{10}^{-2}}T\,.\] If\[\frac{e}{m}\] of electron is \[1.76\times {{10}^{11}}C/kg\]. Then the diameter of the circle will be
A)
11 cm
done
clear
B)
1.1 cm
done
clear
C)
1.1 mm
done
clear
D)
1.1 m
done
clear
View Answer play_arrow
question_answer 19) In an AC circuit the potential difference and current are represented respectively by V=100 sin (100t) volt,\[I=100\sin \left( 100t+\frac{\pi }{3} \right)\]milliampere. The power in the circuit is
A)
2.5 W
done
clear
B)
5 W
done
clear
C)
10 W
done
clear
D)
104 W
done
clear
View Answer play_arrow
question_answer 20) Escape velocity from earths surface is 11 km/s. If radius of a planet is double than that of earth and density is same as that of earth, then the escape velocity from this planet will be
A)
5.5 km/s
done
clear
B)
11 km/s
done
clear
C)
16.5 km/s
done
clear
D)
22 km/s
done
clear
View Answer play_arrow
question_answer 21) The orbital angular momentum of a satellite revolving at a distance r from the centre is L. If the distance is increased to 16r, then the new angular momentum will be
A)
16 L
done
clear
B)
64 L
done
clear
C)
\[\frac{L}{4}\]
done
clear
D)
4 L
done
clear
View Answer play_arrow
question_answer 22) The acceleration of a particle performing SHM is \[12cm/{{s}^{2}}\] at a distance of 3 cm from the mean position. Its time period is
A)
0.5 s
done
clear
B)
1.0 s
done
clear
C)
2.0 s
done
clear
D)
3.14 s
done
clear
View Answer play_arrow
question_answer 23) A soap bubble in vacuum has a radius of 3 cm and another soap bubble in vacuum has a radius of 4 cm. If the two bubbles coalesce under isothermal condition, then the radius of the new bubble is
A)
2.3 cm
done
clear
B)
4.5 cm
done
clear
C)
5 cm
done
clear
D)
7 cm
done
clear
View Answer play_arrow
question_answer 24) A \[10c{{m}^{3}}\] cube floats in water with a height of \[4\,c{{m}^{3}}\] remaining above the surface. The density of the material from which the cube is made is
A)
0.6 g \[c{{m}^{-3}}\]
done
clear
B)
1.0 g\[c{{m}^{-3}}\]
done
clear
C)
0.4 g \[c{{m}^{-3}}\]
done
clear
D)
0.24 g \[c{{m}^{-3}}\]
done
clear
View Answer play_arrow
question_answer 25) The heat flows through a rod of length 50 cm and area of cross-section 5 \[c{{m}^{2}}\]. Its ends are respectively at 25\[^{0}C\] and 125\[^{0}C\]. The coefficient of thermal conductivity of the material rod is \[0.092\text{ }kcal/m{}^\circ C\]. The temperature gradient of the rod is
A)
\[2{}^\circ C/cm\]
done
clear
B)
\[2{}^\circ C/m\]
done
clear
C)
\[20{}^\circ C/cm\]
done
clear
D)
\[{{20}^{o}}C/m\]
done
clear
View Answer play_arrow
question_answer 26) 5 mol of hydrogen gas is heated from 30\[^{0}C\] to 60\[^{0}C\] at constant pressure. Heat given to the gas is (given R = 2 cat/ mol deg)
A)
750 cal
done
clear
B)
630 cal
done
clear
C)
1050 cal
done
clear
D)
1470 cal
done
clear
View Answer play_arrow
question_answer 27) A fish at a depth of 12 cm in water is viewed by an observer on the bank of a lake. To what height the image of the fish is raised? (Refractive index of lake water = \[\frac{4}{3}\])
A)
9 cm
done
clear
B)
12 cm
done
clear
C)
3.8 cm
done
clear
D)
3 cm
done
clear
View Answer play_arrow
question_answer 28) The rest energy of an electron is 0.511 MeV. The electron is accelerated from rest to a velocity 0.5 c. The change in its energy will he
A)
0.026 MeV
done
clear
B)
0.051 MeV
done
clear
C)
0.079 MeV
done
clear
D)
0.105 MeV
done
clear
View Answer play_arrow
question_answer 29) In Millikans oil drop experiment, an oil drop carrying a charge Q is held stationary a potential difference 2400 V between the plates. To keep a drop of half the radius stationary, the potential difference had to be made 600V. What is the charge on the second drop?
A)
\[\frac{Q}{4}\]
done
clear
B)
\[\frac{Q}{2}\]
done
clear
C)
Q
done
clear
D)
\[\frac{3Q}{2}\]
done
clear
View Answer play_arrow
question_answer 30) Band spectrum is characteristic of the
A)
atoms
done
clear
B)
molecules
done
clear
C)
amorphous solids
done
clear
D)
crystalline solids
done
clear
View Answer play_arrow
question_answer 31) As a result of radioactive decay \[_{92}{{U}^{238}}\] is converted into \[_{91}P{{a}^{234}}\]. The particles emitted during this decay are
A)
a proton and a neutron
done
clear
B)
a proton and two \[\alpha \]-particles
done
clear
C)
an\[\alpha -\]particle and a \[\beta \]-particle
done
clear
D)
two p-particles and a proton
done
clear
View Answer play_arrow
question_answer 32) A p-type semiconductor has acceptor levels 57 meV above the valence band. The maximum wavelength of light required to create a hole
A)
\[57\overset{0}{\mathop{A}}\,\]
done
clear
B)
\[57\times {{10}^{-3}}\overset{0}{\mathop{A}}\,\]
done
clear
C)
\[217105\overset{0}{\mathop{A}}\,\]
done
clear
D)
\[11.61\times {{10}^{-33}}\overset{0}{\mathop{A}}\,\]
done
clear
View Answer play_arrow
question_answer 33) In an explosion a body breaks up into pieces of unequal masses. In this case
A)
both parts will have numerically equal momentum
done
clear
B)
lighter part will have more momentum
done
clear
C)
heavier part will have more momentum
done
clear
D)
both parts will have equal kinetic energy
done
clear
View Answer play_arrow
question_answer 34) A force of 10 N acts on a body of mass 20 kg for 10 s. Change in its momentum is
A)
5 kg m/s
done
clear
B)
100 kg m/s
done
clear
C)
200 kg m/s
done
clear
D)
1000 kg m/s
done
clear
View Answer play_arrow
question_answer 35) In which case does the potential energy decrease?
A)
On compressing a spring
done
clear
B)
On stretching a spring
done
clear
C)
On moving a body against gravitational force
done
clear
D)
On the rising of an air bubble in water
done
clear
View Answer play_arrow
question_answer 36) A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
A)
when the mass is at the highest point of the circle
done
clear
B)
when the mass is at the lowest point of the circle
done
clear
C)
when the wire is horizontal
done
clear
D)
at an angle of \[{{\cos }^{-1}}\left( \frac{1}{3} \right)\]from the upward Vertical
done
clear
View Answer play_arrow
question_answer 37) The time taken by AC of 50 Hz in reaching from zero to the maximum value is
A)
\[50\times {{10}^{-3}}s\]
done
clear
B)
\[5\times {{10}^{-3}}s\]
done
clear
C)
\[1\times {{10}^{-3}}s\]
done
clear
D)
\[2\times {{10}^{-3}}s\]
done
clear
View Answer play_arrow
question_answer 38) The molar heat capacity of rock salt at low temperature varies with temperature according to Debyes \[{{T}^{3}}\] law Thus \[C=k\frac{{{T}^{3}}}{{{\theta }^{3}}}\] where k = 1940 J mol\[Jmo{{l}^{-1}}{{k}^{-1}}\] Calculate how much heat is required to raise the temperature of 2 moles of rock salt from 10 K to 50 K
A)
800 J
done
clear
B)
373 J
done
clear
C)
273 J
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 39) The velocity of an electron in the second orbit of sodium atom (atomic number =11) is r. The velocity of an electron in its fifth orbit will be
A)
v
done
clear
B)
\[\frac{22}{5}v\]
done
clear
C)
\[\frac{5}{2}\]
done
clear
D)
\[\frac{2}{5}v\]
done
clear
View Answer play_arrow
question_answer 40) . A charged particle enters a magnetic Held H with its initial velocity making an angle of 45° with H. The path of the particle will be
A)
a straight line
done
clear
B)
a circle
done
clear
C)
an ellipse
done
clear
D)
a helix
done
clear
View Answer play_arrow
question_answer 41) A 10\[\mu F\] capacitor is charged to a potential difference of 50V and is connected to another uncharged capacitor in parallel. Now the common potential difference becomes 20V. The capacitance of second capacitor is
A)
10\[\mu F\]
done
clear
B)
20\[\mu F\]
done
clear
C)
30\[\mu F\]
done
clear
D)
15\[\mu F\]
done
clear
View Answer play_arrow
question_answer 42) An alternating voltage \[E=200\sqrt{2}\sin (100t)V\] is connected to a \[1\,\mu F\] capacitor through an AC ammeter. The reading of ammeter is
A)
10 mA
done
clear
B)
20 mA
done
clear
C)
40 mA
done
clear
D)
80 mA
done
clear
View Answer play_arrow
question_answer 43) In a step-up transformer the turn ratio is 1 : 2. A Leclanche cell (emf 1.5 V) is connected across the primary. The voltage across the secondary is
A)
3.0 V
done
clear
B)
0.75 V
done
clear
C)
zero
done
clear
D)
1.5 V
done
clear
View Answer play_arrow
question_answer 44) If 10% of the current passes through a moving coil galvanometer of resistance \[99\,\Omega \]. Then the shunt resistance will be
A)
9.9\[\Omega \]
done
clear
B)
11\[\Omega \]
done
clear
C)
10 \[\Omega \]
done
clear
D)
9 \[\Omega \]
done
clear
View Answer play_arrow
question_answer 45) How much energy will necessary for making a body of 500 kg escape from the earth? (\[g=9.8\,m/{{s}^{2}},\] radius of the earth \[=6.4\,\times {{10}^{6}}m\])
A)
about \[9.8\times {{10}^{6}}\,J\]
done
clear
B)
about \[6.4\times {{10}^{8}}\,J\]
done
clear
C)
about \[3.1\times {{10}^{10}}\,J\]
done
clear
D)
about \[27.4\times {{10}^{12}}\,J\]
done
clear
View Answer play_arrow
question_answer 46) In a neon discharge tube\[2.9\times {{10}^{18}}N{{e}^{+}}\] ions move to the right each second while \[1.2\times {{10}^{18}}\] electrons move to the left per second, electrons charge is\[1.6\times {{10}^{19}}C\]. The current in the discharge tube is
A)
1 A, towards right
done
clear
B)
0.66 A, towards right
done
clear
C)
0.66 A, towards left
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 47) Water is falling on the blades of a turbine at a rate of 100 kg/s. If the height of the fall is 100 m, the power transferred to the turbine will be approximately
A)
100 kW
done
clear
B)
10 kW
done
clear
C)
1 kW
done
clear
D)
100 W
done
clear
View Answer play_arrow
question_answer 48) A metre scale is standing vertically on the earths surface on one of its end. It now falls on earth without slipping. Find the velocity with which the free end of the scale strikes the earth. \[(g=10\,m/{{s}^{2}})\]
A)
9.8 m/s
done
clear
B)
5.47 m/s
done
clear
C)
4.5 m/s
done
clear
D)
1 m/s
done
clear
View Answer play_arrow
question_answer 49) For germanium crystal, the forbidden energy gap in joule is
A)
\[1.216\times {{10}^{-19}}\]
done
clear
B)
\[1.76\times {{10}^{-19}}\]
done
clear
C)
\[1.6\times {{10}^{-19}}\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 50)
An electron is accelerated through a potential difference of 200 V. If e/ m for the electron be \[1.6\times {{10}^{11}}\] C/kg, the velocity acquired by the electron will be
A)
\[8\times {{10}^{6}}\]m/s
done
clear
B)
\[8\times {{10}^{5}}\]m/s
done
clear
C)
\[5.9\times {{10}^{6}}\] m/s
done
clear
D)
\[5.9\times {{10}^{5}}\] m/s
done
clear
View Answer play_arrow
question_answer 51) At what temperature will the resistance of a copper wire become three times its value at \[0{}^\circ C\]? (temperature coefficient of resistance for copper = \[4\times {{10}^{-3}}{{/}^{0}}C\])
A)
\[{{400}^{\text{o}}}C\]
done
clear
B)
\[{{450}^{\text{o}}}C\]
done
clear
C)
\[{{500}^{\text{o}}}C\]
done
clear
D)
\[{{550}^{\text{o}}}C\]
done
clear
View Answer play_arrow
question_answer 52) A coil having an area of \[2{{m}^{2}}\] is placed in a magnetic field which changes from \[1\,Wb/{{m}^{2}}\] to \[4\,Wb/{{m}^{2}}\,\] in 2 s. The emf induced in the coil will be
A)
4 V
done
clear
B)
3 V
done
clear
C)
2 V
done
clear
D)
1 V
done
clear
View Answer play_arrow
question_answer 53) A 10 m long copper wire while remaining in the east-west horizontal direction is falling down with a speed of 5.0 m/s. If the horizontal component of the earths magnetic field \[=0.3\times {{10}^{-4}}Wb/{{m}^{2}}\]the emf developed between the ends of the wires is
A)
0.15 V
done
clear
B)
1.5 V
done
clear
C)
0.15 mV
done
clear
D)
1.5 mV
done
clear
View Answer play_arrow
question_answer 54) A current of 1.6 A is passed through a solution of\[CuS{{O}_{4}}\]. How many \[C{{u}^{++}}\] ions are liberated in one minute? (electronic charge = \[1.6\times {{10}^{-19}}C\])
A)
\[3\times {{10}^{20}}\]
done
clear
B)
\[3\times {{10}^{19}}\]
done
clear
C)
\[6\times {{10}^{20}}\]
done
clear
D)
\[6\times {{10}^{19}}\]
done
clear
View Answer play_arrow
question_answer 55) A solenoid has an inductance of 60 H and a resistance of 30\[\Omega \]. If it is connected to a 100 V battery, how long will it take for the current to reach \[\frac{e-1}{e}\]= 63.2% of its final value?
A)
1 s
done
clear
B)
2 s
done
clear
C)
e second
done
clear
D)
2 e second
done
clear
View Answer play_arrow
question_answer 56)
Three blocks of masses \[{{m}_{1}},\,{{m}_{2}}\] are connected by massless strings as shown on a frictionless table. They are pulled with a force \[{{T}_{3}}\]= 40 N. If \[{{m}_{1}}=10\,kg,{{m}_{2}}=6\,kg\] and \[{{m}_{3}}=4\,kg,\] the tension \[{{T}_{2}}\]will be
A)
20 N
done
clear
B)
40 N
done
clear
C)
10 N
done
clear
D)
32 N
done
clear
View Answer play_arrow
question_answer 57) The force constant of weightless spring is 16 N/m. A body of mass 1.0 kg suspended from it is pulled down through 5 cm and then released. The maximum kinetic energy of the system (spring + body) will be
A)
\[2\times {{10}^{-2}}J\]
done
clear
B)
\[4\times {{10}^{-2}}J\]
done
clear
C)
\[8\times {{10}^{-2}}J\]
done
clear
D)
\[16\times {{10}^{-2}}J\]
done
clear
View Answer play_arrow
question_answer 58) A mass M is moving with a constant velocity on a line parallel to the x-axis. Its angular momentum with respect to the origin or z-axis
A)
is zero
done
clear
B)
remains constant
done
clear
C)
goes on increasing
done
clear
D)
goes on decreasing
done
clear
View Answer play_arrow
question_answer 59) Which of the following pairs is an isobar?
A)
\[_{1}{{H}^{1\,\,}}and\,{{\,}_{1}}{{H}^{2}}\]
done
clear
B)
\[_{1}{{H}^{2\,\,}}and\,{{\,}_{1}}{{H}^{3}}\]
done
clear
C)
\[_{6}{{C}^{12\,\,}}and\,{{\,}_{6}}{{H}^{13}}\]
done
clear
D)
\[_{15}{{P}^{30\,\,}}and\,{{\,}_{14}}S{{i}^{30}}\]
done
clear
View Answer play_arrow
question_answer 60) The half-life of the isotope \[_{11}N{{a}^{24\,\,}}\]is 15 h. How much time does it take for \[\frac{7}{8}\] th of a sample of this isotope to decay?
A)
75 h
done
clear
B)
65 h
done
clear
C)
55 h
done
clear
D)
45 h
done
clear
View Answer play_arrow
question_answer 61) The largest number of molecules is in
A)
\[36\,\,g\]of water
done
clear
B)
\[28\,\,g\]of\[C{{O}_{2}}\]
done
clear
C)
\[46\,\,g\]of\[C{{H}_{3}}OH\]
done
clear
D)
\[58\,\,g\]of\[{{N}_{2}}{{O}_{5}}\]
done
clear
View Answer play_arrow
question_answer 62) In the following reaction, which choice has value twice that of the equivalent weight of the oxidizing agent? \[S{{O}_{2}}+2{{H}_{2}}O\xrightarrow{{}}S+2{{H}_{2}}{{O}_{2}}\]
A)
16
done
clear
B)
48
done
clear
C)
64
done
clear
D)
32
done
clear
View Answer play_arrow
question_answer 63) Orbital is
A)
circular path around the nucleus in which electrons are revolves
done
clear
B)
space around the nucleus, where the probability of finding the electron is maximum
done
clear
C)
amplitude of electrons wave
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 64) Which of the following sets of quantum number is not permitted?
A)
\[n=3,\,\,l=3,\,\,m=0,\,\,s=+\frac{1}{2}\]
done
clear
B)
\[n=3,\,\,l=2,\,\,m=\pm 2,\,\,s=-\frac{1}{2}\]
done
clear
C)
\[n=3,\,\,l=2,\,\,m=-2,\,\,s=-\frac{1}{2}\]
done
clear
D)
\[n=3,\,\,l=0,\,\,m=0,\,\,s=+\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 65) An element M has an atomic mass of 19 and atomic number 9, its ions is represented by
A)
\[{{M}^{+}}\]
done
clear
B)
\[{{M}^{2+}}\]
done
clear
C)
\[{{M}^{-}}\]
done
clear
D)
\[{{M}^{2-}}\]
done
clear
View Answer play_arrow
question_answer 66) In sq molecules, the type of hybridisation exhibited by sulphur is
A)
\[s{{p}^{2}}\]
done
clear
B)
\[s{{p}^{3}}\]
done
clear
C)
\[sp\]
done
clear
D)
\[s{{p}^{3}}d\]
done
clear
View Answer play_arrow
question_answer 67) In the oxyacids of chlorine,\[Cl-O\]bond contains
A)
\[d\pi -d\pi \]bonding
done
clear
B)
\[d\pi -p\pi \]bonding
done
clear
C)
\[p\pi -p\pi \]bonding
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 68) Anhydrous\[AlC{{l}_{3}}\]fume in air due to
A)
oxidation
done
clear
B)
hydrolysis
done
clear
C)
reduction
done
clear
D)
hydrogenation
done
clear
View Answer play_arrow
question_answer 69) The nature of\[F{{e}_{2}}{{O}_{3}}\]is
A)
acidic
done
clear
B)
basic
done
clear
C)
amphoteric
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 70) Concentrated nitric acid \[(HN{{O}_{3}})\] oxidizes phosphorus to
A)
\[{{H}_{3}}P{{O}_{4}}\]
done
clear
B)
\[{{H}_{3}}P{{O}_{3}}\]
done
clear
C)
\[{{H}_{4}}{{P}_{2}}{{O}_{7}}\]
done
clear
D)
\[{{H}_{3}}P{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 71) Which of the following has the highest nucleophilicity?
A)
\[{{F}^{-}}\]
done
clear
B)
\[O{{H}^{-}}\]
done
clear
C)
\[CH_{3}^{-}\]
done
clear
D)
\[NH_{2}^{-}\]
done
clear
View Answer play_arrow
question_answer 72) Number of isomeric primary amines obtained from\[{{C}_{4}}{{H}_{11}}N\]are
A)
3
done
clear
B)
4
done
clear
C)
5
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 73) Which of the following reaction doesnt support the acidic nature of alkyne?
A)
Reaction with\[HBr\]
done
clear
B)
Reaction with Grignard reagent
done
clear
C)
Reaction with ammoniacal silver salt
done
clear
D)
Reaction with metallic sodium
done
clear
View Answer play_arrow
question_answer 74) \[C{{H}_{3}}-C{{H}_{2}}-\underset{\begin{smallmatrix} | \\ C{{H}_{3}} \end{smallmatrix}}{\mathop{N}}\,-\overset{\begin{smallmatrix} O \\ || \end{smallmatrix}}{\mathop{C}}\,-H;\] The\[IUPAC\]name of the compound is
A)
N-formyl-N-methyl ethanamide
done
clear
B)
N-ethyl-N-methyl methanamide
done
clear
C)
N-methyl-N-oxo ethanamine
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 75) The product of the following reaction,\[{{C}_{6}}{{H}_{5}}COCHB{{r}_{2}}\xrightarrow{O{{H}^{-}}}?\]is
A)
\[{{C}_{6}}{{H}_{5}}COCHO\]
done
clear
B)
\[{{C}_{6}}{{H}_{5}}COCOOH\]
done
clear
C)
\[{{C}_{6}}{{H}_{5}}CHO\]
done
clear
D)
\[{{C}_{6}}{{H}_{5}}CHOHCOOH\]
done
clear
View Answer play_arrow
question_answer 76)
Which of the following alkenes will react fastest with
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 77) Glucose reacts with acetic anhydride to give pentaacetyl derivative. Which of the following is true about that?
A)
that can reduce Fehling or Tollens reagent
done
clear
B)
thats soluble in dil. \[NaOH\] solution
done
clear
C)
that consumes one mole of \[HI{{O}_{4}}\]
done
clear
D)
\[B{{r}_{2}}/{{H}_{2}}O\]can oxidize
done
clear
View Answer play_arrow
question_answer 78) Complete hydrolysis of cellulose gives
A)
D-fructose
done
clear
B)
D-ribose
done
clear
C)
D-glucose
done
clear
D)
L-glucose
done
clear
View Answer play_arrow
question_answer 79) The saponification value of an oil or fat is measured in terms of
A)
\[N{{H}_{4}}OH\]
done
clear
B)
\[NaOH\]
done
clear
C)
\[{{C}_{6}}{{H}_{5}}OH\]
done
clear
D)
\[kOH\]
done
clear
View Answer play_arrow
question_answer 80) \[{{N}_{2}}\]gas is liberated when\[[HCl+NaN{{O}_{2}}]\]reacts with the following compounds; \[A.C{{H}_{3}}C{{H}_{2}}N{{H}_{2}}\] \[B.\,\,urea\] \[C.C{{H}_{3}}CON{{H}_{2}}\] \[D.{{C}_{6}}{{H}_{5}}N{{H}_{2}}\] The answer is
A)
A, B, C
done
clear
B)
B, C, D
done
clear
C)
A, C, D
done
clear
D)
A, B, D
done
clear
View Answer play_arrow
question_answer 81) Benzaldehyde condenses with \[N,\,\,N\]dimethyl aniline in presence of anhydrous\[ZnC{{l}_{2}}\]to give
A)
azo dye
done
clear
B)
malachite
done
clear
C)
michlers ketone
done
clear
D)
buffer yellow
done
clear
View Answer play_arrow
question_answer 82) Which of the following reactions is given by only primary amines?
A)
Reaction with\[HN{{O}_{2}}\]
done
clear
B)
Reaction with chloroform and alcoholic\[KOH\]
done
clear
C)
Reaction with acetyl chloride
done
clear
D)
Reaction with Grignard reagent
done
clear
View Answer play_arrow
question_answer 83) \[C{{H}_{3}}COOH\xrightarrow{N{{H}_{3}}}\xrightarrow{\Delta }?\] The product of the reaction is isomeric with
A)
\[\underset{\begin{smallmatrix} | \\ N{{H}_{2}} \end{smallmatrix}}{\mathop{C{{H}_{2}}}}\,-CHO\]
done
clear
B)
\[C{{H}_{3}}CH=NOH\]
done
clear
C)
\[HCONH-C{{H}_{3}}\]
done
clear
D)
All of these
done
clear
View Answer play_arrow
question_answer 84) Which one of the following compound gives aspirin on reacting with acetic anhydride in presence of\[{{H}_{2}}S{{O}_{4}}\]?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 85)
A)
\[Cl\]
done
clear
B)
\[N{{H}_{2}}\]
done
clear
C)
\[O{{C}_{2}}{{H}_{5}}\]
done
clear
D)
\[OCO{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 86) Aldehyde not showing cannizzaros reaction is
A)
paraldehyde
done
clear
B)
chloral
done
clear
C)
formaldehyde
done
clear
D)
acetaldehyde
done
clear
View Answer play_arrow
question_answer 87) Both\[HCHO\]and\[C{{H}_{3}}CHO\]gives similar reactions with all the reagents except
A)
Schiff reagent
done
clear
B)
Fehling solution
done
clear
C)
ammoniacal\[AgN{{O}_{3}}\]
done
clear
D)
ammonia
done
clear
View Answer play_arrow
question_answer 88) Which of the following statements is not correct?
A)
All alcohols are miscible with water
done
clear
B)
Only lower alcohols are miscible with water
done
clear
C)
All alcohols are not poisonous
done
clear
D)
Methanol is poisonous
done
clear
View Answer play_arrow
question_answer 89) Cyclohexanol is
A)
phenol
done
clear
B)
\[1{}^\circ \]alcohol
done
clear
C)
\[2{}^\circ \]alcohol
done
clear
D)
\[3{}^\circ \]alcohol
done
clear
View Answer play_arrow
question_answer 90) In the manufacture of ethanol from sugar the enzymes are
A)
diastase and zymase
done
clear
B)
maltase and zymase
done
clear
C)
diastase and invertase
done
clear
D)
invertase and zymase
done
clear
View Answer play_arrow
question_answer 91) The action of chloral on chlorobenzene gives
A)
BHC
done
clear
B)
DDT
done
clear
C)
gammexene
done
clear
D)
lindane
done
clear
View Answer play_arrow
question_answer 92) Which halide will be least reactive in respect to hydrolysis?
A)
vinyl chloride
done
clear
B)
allyl chloride
done
clear
C)
ethyl chloride
done
clear
D)
\[t-\]butyl chloride
done
clear
View Answer play_arrow
question_answer 93) By Wurtz reaction, a mixture of methyl iodide and ethyl iodide gives
A)
butane
done
clear
B)
ethane
done
clear
C)
propane
done
clear
D)
a mixture of above three
done
clear
View Answer play_arrow
question_answer 94) The cyanide process is used for obtaining
A)
\[Cu\]
done
clear
B)
\[Na\]
done
clear
C)
\[Zn\]
done
clear
D)
\[Ag\]
done
clear
View Answer play_arrow
question_answer 95) Which of the following ore does not represent the ores of iron?
A)
Cassiterite
done
clear
B)
Limonite
done
clear
C)
Haematite
done
clear
D)
Magnetite
done
clear
View Answer play_arrow
question_answer 96) van-Arkel method of purification of metals involves converting the metal to a
A)
volatile stable compound
done
clear
B)
non-volatile stable compound
done
clear
C)
volatile unstable compound
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 97) The first element of rare earth metal is
A)
cerium
done
clear
B)
cesium
done
clear
C)
lanthanide
done
clear
D)
actinide
done
clear
View Answer play_arrow
question_answer 98) Which of the following transitions involves maximum amount of energy?
A)
\[{{M}^{-}}(g)\xrightarrow{{}}M(g)\]
done
clear
B)
\[{{M}^{-}}(g)\xrightarrow{{}}{{M}^{+}}(g)\]
done
clear
C)
\[{{M}^{+}}(g)\xrightarrow{{}}{{M}^{2+}}(g)\]
done
clear
D)
\[{{M}^{2+}}(g)\xrightarrow{{}}{{M}^{3+}}(g)\]
done
clear
View Answer play_arrow
question_answer 99) Transition metal with low oxidation number will act as
A)
an oxidizing agent
done
clear
B)
a base
done
clear
C)
an acid
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 100) Chloride of which of the following element is colored?
A)
\[Hg\]
done
clear
B)
\[Ag\]
done
clear
C)
\[Co\]
done
clear
D)
\[Zn\]
done
clear
View Answer play_arrow
question_answer 101) Spiegeleisn is an alloy of
A)
\[Fe,Co\]and\[Cr\]
done
clear
B)
\[Fe,Co\] and\[Mg\]
done
clear
C)
\[Fe,Mg\]and\[C\]
done
clear
D)
\[Fe,C\]and\[Mn\]
done
clear
View Answer play_arrow
question_answer 102) Which of the following ions form most stable complex compound?
A)
\[M{{n}^{2+}}\]
done
clear
B)
\[N{{i}^{2+}}\]
done
clear
C)
\[F{{e}^{2+}}\]
done
clear
D)
\[C{{u}^{2+}}\]
done
clear
View Answer play_arrow
question_answer 103) Coordination number of\[Fe\]in the complexes \[{{[Fe{{(CN)}_{6}}]}^{4-}}\],\[{{[Fe{{(CN)}_{6}}]}^{3-}}\]and\[{{[FeC{{l}_{4}}]}^{-}}\]would be respectively
A)
6, 4, 6
done
clear
B)
6, 6, 4
done
clear
C)
6, 3, 3
done
clear
D)
2, 3, 3
done
clear
View Answer play_arrow
question_answer 104) Which of the following is a wrong statement?
A)
\[Ni{{(CO)}_{4}}\]has zero oxidation number for\[Ni\]
done
clear
B)
\[Ni{{(CO)}_{4}}\]has oxidation number\[+4\]for\[Ni\]
done
clear
C)
\[Ni\]is metal
done
clear
D)
\[CO\]is gas
done
clear
View Answer play_arrow
question_answer 105) Rusting of iron is catalyzed by which of the following?
A)
\[Fe\]
done
clear
B)
\[Zn\]
done
clear
C)
\[{{O}_{2}}\]
done
clear
D)
\[{{H}^{+}}\]
done
clear
View Answer play_arrow
question_answer 106) Standard electrode potential of\[NHE\]at\[298\,\,K\]is
A)
\[0.05\,\,V\]
done
clear
B)
\[0.10\,\,V\]
done
clear
C)
\[0.50\,\,V\]
done
clear
D)
\[0.00\,\,V\]
done
clear
View Answer play_arrow
question_answer 107) For a cell reaction involving a two electron change, the standard emf of the cell is found to be\[0.295\,\,V\]at\[{{25}^{o}}C\]. The equilibrium constant of the reaction at\[{{25}^{o}}C\]will be
A)
\[10\]
done
clear
B)
\[1\times {{10}^{10}}\]
done
clear
C)
\[1\times {{10}^{-10}}\]
done
clear
D)
\[10\times {{10}^{-2}}\]
done
clear
View Answer play_arrow
question_answer 108) The ionic conductance of\[B{{a}^{2+}}\]and\[C{{l}^{-}}\]are respectively\[127\]and\[76\,\,oh{{m}^{-1}}-c{{m}^{2}}\]at infinite dilution. The equivalent conductance\[(in\,\,oh{{m}^{-1}}\,\,c{{m}^{2}})\]of\[BaC{{l}_{2}}\]at infinite dilution will be
A)
139.5
done
clear
B)
203
done
clear
C)
279
done
clear
D)
101.5
done
clear
View Answer play_arrow
question_answer 109) Multimolecular colloids are present in
A)
soap solution
done
clear
B)
sol of proteins
done
clear
C)
sol of gold
done
clear
D)
All of these
done
clear
View Answer play_arrow
question_answer 110) In physical adsorption, the gas molecules are held by solid surfaces through
A)
strong chemical forces
done
clear
B)
van der waals forces
done
clear
C)
metallic bonds
done
clear
D)
gravitational forces
done
clear
View Answer play_arrow
question_answer 111) The osmotic pressure of a 5% (wt./vol.) solution of cane sugar at\[{{150}^{o}}C\]is
A)
\[3.078\,\,atm\]
done
clear
B)
\[4.078\,\,atm\]
done
clear
C)
\[5.078\,\,atm\]
done
clear
D)
\[2.45\,\,atm\]
done
clear
View Answer play_arrow
question_answer 112) The mole fraction of water in 20% aqueous solution of\[{{H}_{2}}{{O}_{2}}\]is
A)
\[\frac{20}{80}\]
done
clear
B)
\[\frac{80}{20}\]
done
clear
C)
\[\frac{34}{77}\]
done
clear
D)
\[\frac{77}{68}\]
done
clear
View Answer play_arrow
question_answer 113) The\[pH\]of a solution is increased from 3 to 6, its\[{{H}^{+}}\]ion concentration will be
A)
reduced to half
done
clear
B)
doubled
done
clear
C)
reduced by 1000 times
done
clear
D)
increased by 1000 times
done
clear
View Answer play_arrow
question_answer 114) Solubility product of\[BaC{{l}_{2}}\]is\[4\times {{10}^{-9}}\]. Its solubility in mol/L would be
A)
\[1\times {{10}^{-3}}\]
done
clear
B)
\[1\times {{10}^{-9}}\]
done
clear
C)
\[4\times {{10}^{-27}}\]
done
clear
D)
\[1\times {{10}^{-27}}\]
done
clear
View Answer play_arrow
question_answer 115) An example of a Lewis acid is
A)
\[NaCl\]
done
clear
B)
\[MgC{{l}_{2}}\]
done
clear
C)
\[AlC{{l}_{3}}\]
done
clear
D)
\[SnC{{l}_{4}}\]
done
clear
View Answer play_arrow
question_answer 116) Radioactive decay is a
A)
first order reaction
done
clear
B)
zero order reaction
done
clear
C)
second order reaction
done
clear
D)
third order reaction
done
clear
View Answer play_arrow
question_answer 117) The rate constant for the first order reaction is\[60{{s}^{-1}}\]. How much time will it take to reduce the concentration of the reactant to\[\frac{1}{16}th\]value?
A)
\[4.6\times {{10}^{-2}}s\]
done
clear
B)
\[4.6\times {{10}^{4}}s\]
done
clear
C)
\[4.6\times {{10}^{2}}s\]
done
clear
D)
\[4.6\times {{10}^{-4}}s\]
done
clear
View Answer play_arrow
question_answer 118) \[(\Delta H-\Delta U)\]for the formation of carbon monoxide\[(CO)\]from its elements at\[298\,\,K\]is\[(R=8.314\,\,J{{K}^{-1}}mo{{l}^{-1}})\]
A)
\[-1238.78\,\,J\,\,mo{{l}^{-1}}\]
done
clear
B)
\[1238.78\,\,J\,\,mo{{l}^{-1}}\]
done
clear
C)
\[-2477.57\,\,J\,\,mo{{l}^{-1}}\]
done
clear
D)
\[2477.57\,\,J\,\,mo{{l}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 119) An ideal gas at constant temperature and pressure expands, then its
A)
internal energy remains same
done
clear
B)
internal energy decrease
done
clear
C)
internal energy increases
done
clear
D)
entropy first increases and then decreases
done
clear
View Answer play_arrow
question_answer 120) At which temperature nitrogen under \[1.00\,\,atm\] pressure has the same root mean square speed as that of\[C{{O}_{2}}\]at\[STP\]
A)
\[{{0}^{o}}C\]
done
clear
B)
\[{{27}^{o}}C\]
done
clear
C)
\[-{{99}^{o}}C\]
done
clear
D)
\[-{{200}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 121) The value of\[\left| \begin{matrix} {{a}^{2}} & {{b}^{2}} & {{c}^{2}} \\ {{(a+1)}^{2}} & {{(b+1)}^{2}} & {{(c+1)}^{2}} \\ {{(a-1)}^{2}} & {{(b-1)}^{2}} & {{(c-1)}^{2}} \\ \end{matrix} \right|\]is
A)
\[3\left| \begin{matrix} {{a}^{2}} & {{b}^{2}} & {{c}^{2}} \\ a & b & c \\ 1 & 1 & 1 \\ \end{matrix} \right|\]
done
clear
B)
\[3\left| \begin{matrix} {{a}^{2}} & {{b}^{2}} & {{c}^{2}} \\ a & b & c \\ 1 & 1 & 1 \\ \end{matrix} \right|\]
done
clear
C)
\[2\left| \begin{matrix} {{a}^{2}} & {{b}^{2}} & {{c}^{2}} \\ a & b & c \\ 1 & 1 & 1 \\ \end{matrix} \right|\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 122) If\[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z=0\],\[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z=0\]\[{{a}_{3}}x+{{b}_{3}}y+{{c}_{3}}z=0\]and\[\left| \begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}} \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}} \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}} \\ \end{matrix} \right|=0\], then the given system has
A)
one trivial and one non-trivial solution
done
clear
B)
no solution
done
clear
C)
one solution
done
clear
D)
infinite solution
done
clear
View Answer play_arrow
question_answer 123) Let\[A\]be a square matrix all of whose entries are integers. Then, which one of the following is true?
A)
If\[\det (A)=\pm 1\], then\[{{A}^{-1}}\]exists but all its entries are not necessarily integers
done
clear
B)
If\[\det (A)\ne \pm 1\], then\[{{A}^{-1}}\].exists and all its entries are non-integers
done
clear
C)
If\[\det (A)=\pm 1\], then\[{{A}^{-1}}\]exists and all its entries are integers
done
clear
D)
If\[\det (A)=\pm 1\], then\[{{A}^{-1}}\]need not exist
done
clear
View Answer play_arrow
question_answer 124) Which of the following statements is/are correct? I. Adjoint of a unit matrix is a unit matrix. II. \[A(adj\,\,A)=(adj\,\,A)A=|A|\,\,I\] III. Adjoint of a symmetric matrix is symmetric. IV. Adjoint of a diagonal matrix is a diagonal matrix.
A)
I
done
clear
B)
II
done
clear
C)
I or II
done
clear
D)
All statements are correct
done
clear
View Answer play_arrow
question_answer 125) The value of\[\int{\frac{dx}{x\sqrt{1-{{(\log x)}^{2}}}}}\]is
A)
\[{{\cos }^{-1}}(\log x+C)\]
done
clear
B)
\[x\log (1-{{x}^{2}})+C\]
done
clear
C)
\[\frac{1}{2}{{\cos }^{-1}}(\log x+C)\]
done
clear
D)
\[{{\sin }^{-1}}(\log x+C)\]
done
clear
View Answer play_arrow
question_answer 126) \[\int{\frac{{{x}^{2}}}{({{x}^{2}}+2)({{x}^{2}}+3)}dx}\]is equal to
A)
\[-\sqrt{2}{{\tan }^{-1}}\left( \frac{x}{\sqrt{2}} \right)+\sqrt{3}{{\tan }^{-1}}\left( \frac{x}{\sqrt{3}} \right)+C\]
done
clear
B)
\[\sqrt{2}{{\tan }^{-1}}\left( \frac{x}{\sqrt{2}} \right)+\sqrt{3}{{\tan }^{-1}}\left( \frac{x}{\sqrt{3}} \right)+C\]
done
clear
C)
\[-\sqrt{2}{{\tan }^{-1}}x+\sqrt{3}{{\tan }^{-1}}x+C\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 127) The degree and order of the differential equation of the family of all parabolas whose axis is x-axis, are respectively
A)
2, 1
done
clear
B)
1, 2
done
clear
C)
3, 2
done
clear
D)
2, 3
done
clear
View Answer play_arrow
question_answer 128) The differential equation satisfied by the family of curve\[y=ax\cos \left( \frac{1}{x}+b \right)\], where\[a,\,\,b\]are parameters, is
A)
\[{{x}^{2}}{{y}_{2}}+y=0\]
done
clear
B)
\[{{x}^{4}}+{{y}_{2}}+y=0\]
done
clear
C)
\[x{{y}_{2}}-y=0\]
done
clear
D)
\[{{x}^{4}}{{y}_{2}}-y=0\]
done
clear
View Answer play_arrow
question_answer 129) Integrating factor of equation\[({{x}^{2}}+1)\frac{dy}{dx}+2xy={{x}^{2}}-1\]is
A)
\[\frac{2x}{{{x}^{2}}+1}\]
done
clear
B)
\[\frac{{{x}^{2}}-1}{{{x}^{2}}+1}\]
done
clear
C)
\[{{x}^{2}}+1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 130) The value of\[\int_{0}^{\pi /2}{|\sin x-\cos x|}\,\,dx\]is
A)
\[0\]
done
clear
B)
\[2(\sqrt{2}-1)\]
done
clear
C)
\[\sqrt{2}-1\]
done
clear
D)
\[2(\sqrt{2}+1)\]
done
clear
View Answer play_arrow
question_answer 131) The equation of the circle which passes through the points (2, 3) and (4, 5) and the centre lies on the straight line\[y-4x+3=0\], is
A)
\[{{x}^{2}}+{{y}^{2}}+4x-10y+25=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-4x-10y+16=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-4x-10y+25=0\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 132) The number of solutions of\[{{\log }_{4}}(x-1)={{\log }_{2}}(x-3)\]is/ are
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 133) If\[\alpha ,\,\,\beta \]are the roots of\[{{x}^{2}}-3x+1=0\], then the equation whose roots are\[\frac{1}{\alpha -2},\,\,\frac{1}{\beta -2}\]is
A)
\[{{x}^{2}}+x+1=0\]
done
clear
B)
\[{{x}^{2}}-x-1=0\]
done
clear
C)
\[{{x}^{2}}+x-1=0\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 134) If\[x\]is real/then the value of\[\frac{{{x}^{2}}+34x-71}{{{x}^{2}}+2x-7}\]does not lie between
A)
8 and -5
done
clear
B)
-5 and 9
done
clear
C)
0 and 9
done
clear
D)
5 and 9
done
clear
View Answer play_arrow
question_answer 135) The square root of\[\sqrt{50}+\sqrt{48}\]is
A)
\[{{2}^{1/4}}(3+\sqrt{2})\]
done
clear
B)
\[{{2}^{1/4}}(\sqrt{3}+\sqrt{2})\]
done
clear
C)
\[{{2}^{1/4}}(2+\sqrt{2})\]
done
clear
D)
\[{{2}^{1/4}}(\sqrt{3}+2)\]
done
clear
View Answer play_arrow
question_answer 136) Let\[{{I}_{1}}=\int_{\alpha }^{\pi -\alpha }{xf}(\sin x)\,\,dx,\,\,{{I}_{2}}\]\[=\int_{xf(\sin x)\,\,dx}^{\pi -\alpha }{f(\sin x)}\,\,dx\], then \[{{I}_{2}}\] is equal to
A)
\[\frac{\pi }{2}{{I}_{1}}\]
done
clear
B)
\[\pi {{I}_{1}}\]
done
clear
C)
\[\frac{2}{\pi }{{I}_{1}}\]
done
clear
D)
\[2{{I}_{1}}\]
done
clear
View Answer play_arrow
question_answer 137) The area of figure bounded by\[y={{e}^{x}},\,\,y={{e}^{-x}}\]and the straight line\[x=1\]is
A)
\[\left( e+\frac{1}{e} \right)sq\,\,unit\]
done
clear
B)
\[\left( e-\frac{1}{e} \right)sq\,\,unit\]
done
clear
C)
\[\left( e+\frac{1}{e}-2 \right)sq\,\,unit\]
done
clear
D)
\[\left( e+\frac{1}{e}+2 \right)sq\,\,unit\]
done
clear
View Answer play_arrow
question_answer 138) The domain and range of\[f(x)={{\sin }^{-1}}[x]\]are
A)
\[[0,\,\,2),\,\,\left\{ -\frac{\pi }{2},\,\,\frac{\pi }{2} \right\}\]
done
clear
B)
\[[-1,\,\,2)\left\{ -\frac{\pi }{2},\,\,0,\,\,\frac{\pi }{2} \right\}\]
done
clear
C)
\[[-1,\,\,2)\left\{ -\pi ,\,\,\frac{-\pi }{2},\,\,0,\,\,\frac{\pi }{2},\,\,\pi \right\}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 139) If\[\mathbf{a,}\,\,\mathbf{b}\]and\[\mathbf{c}\]are non-collinear vectors such that for some scalars\[\text{x,}\,\,\text{y,}\,\,\text{z,}\,\,x\mathbf{a}+x\mathbf{b}+x\mathbf{c}=0\], then
A)
\[x=0,\,\,y=0,\,\,z=0\]
done
clear
B)
\[x\ne 0,\,\,y\ne 0,\,\,z=0\]
done
clear
C)
\[x=0,\,\,y\ne 0,\,\,z\ne 0\]
done
clear
D)
\[x\ne 0,\,\,y\ne 0,\,\,z\ne 0\]
done
clear
View Answer play_arrow
question_answer 140) Let\[\mathbf{a,}\,\,\mathbf{b,}\,\,\mathbf{c}\]be three vectors such that\[\mathbf{c}\ne 0\]and \[\mathbf{a}\cdot \mathbf{b}\]\[=2\mathbf{a}\cdot \mathbf{c},\,\,|\mathbf{a}|=|\mathbf{c}|=1,\,\,|\mathbf{b}|=4\]and\[\mathbf{|b\times c|}=\sqrt{15}\], if\[\mathbf{b}-2\mathbf{c}=\lambda \alpha \] then,\[\lambda \]equals
A)
-1
done
clear
B)
1
done
clear
C)
-4
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 141) The image of the point with position vector\[\mathbf{i}+3\mathbf{k}\]in the plane\[r\cdot (\mathbf{i}+\mathbf{j}+\mathbf{k})=1\]is
A)
\[\mathbf{i}-2\mathbf{j}+\mathbf{k}\]
done
clear
B)
\[\mathbf{i}+2\mathbf{j}-\mathbf{k}\]
done
clear
C)
\[-\mathbf{i}-2\mathbf{j}+\mathbf{k}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 142) The vectors\[\mathbf{c},\,\,\mathbf{a},\,\,=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\]and\[\mathbf{b}=\mathbf{j}\]are such that\[\mathbf{a},\,\,\mathbf{b},\,\,\mathbf{c}\]form a right handed system, then\[\mathbf{c}\]is
A)
\[0\]
done
clear
B)
\[y\,\,\mathbf{j}\]
done
clear
C)
\[-z\,\,\mathbf{i}+x\,\,\mathbf{k}\]
done
clear
D)
\[z\,\,\mathbf{i}-x\,\,\mathbf{k}\]
done
clear
View Answer play_arrow
question_answer 143) The equation of plane passing through a point \[A\](2, -1, 3) and parallel to the vectors \[\mathbf{a}=(3,\,\,0,\,\,-1)\]and\[\mathbf{b}=(-3,\,\,2,\,\,2)\]is
A)
\[2x-3y+6z+25=0\]
done
clear
B)
\[3x-2y+6z+25=0\]
done
clear
C)
\[2x-3y+6z-25=0\]
done
clear
D)
\[3x-2y+6z-25=0\]
done
clear
View Answer play_arrow
question_answer 144) \[\underset{x\to 1}{\mathop{\lim }}\,\frac{(2x-3)(\sqrt{x}-1)}{2{{x}^{2}}+x-3}\]is equal to
A)
\[-1/10\]
done
clear
B)
\[1/10\]
done
clear
C)
\[-1/8\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 145) Which is the correct order for a given number a in increasing order?
A)
\[{{\log }_{2}}\alpha ,\,\,{{\log }_{3}}\alpha ,\,\,{{\log }_{e}}\alpha ,\,\,{{\log }_{10}}\alpha \]
done
clear
B)
\[{{\log }_{10}}\alpha ,\,\,{{\log }_{3}}\alpha ,\,\,{{\log }_{e}}\alpha ,\,\,{{\log }_{2}}\alpha \]
done
clear
C)
\[{{\log }_{10}}\alpha ,\,\,{{\log }_{e}}\alpha ,\,\,{{\log }_{2}}\alpha ,\,\,\alpha {{\log }_{3}}\alpha \]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 146) If\[x=\frac{\sqrt{5}+\sqrt{2}}{\sqrt{5}-\sqrt{2}},\,\,y=\frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}+\sqrt{2}}\]then \[3{{x}^{2}}+4xy\,-3{{y}^{2}}\] is equal to
A)
\[\frac{1}{3}(56\sqrt{10}+12)\]
done
clear
B)
\[\frac{1}{3}(56\sqrt{10}-12)\]
done
clear
C)
\[\frac{1}{3}(56+12\sqrt{10})\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 147) If\[x+y=1\], then\[\sum\limits_{r=0}^{n}{{{r}^{2\cdot n}}}{{C}_{r}}{{x}^{r}}-{{y}^{n-r}}\]is equal to
A)
\[nxy\]
done
clear
B)
\[nx(x+yn)\]
done
clear
C)
\[nx(n\,\,x+y)\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 148) If\[Z=f(x+ay)+\phi (x-ay)\], then
A)
\[{{Z}_{xx}}={{Z}_{yy}}\]
done
clear
B)
\[{{Z}_{xx}}={{a}^{2}}{{Z}_{yy}}\]
done
clear
C)
\[{{Z}_{yy}}={{a}^{2}}{{Z}_{xx}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 149) The existence of the unique solution of the system\[x+y+z=\lambda \],\[5x-y+\mu z=10\]\[2x+3y-z=6\]depends on
A)
\[\mu \]only
done
clear
B)
\[\lambda \]only
done
clear
C)
\[\lambda \]and\[\mu \]both
done
clear
D)
neither\[\lambda \]nor\[\mu \]
done
clear
View Answer play_arrow
question_answer 150) Let\[A=\left| \begin{matrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1 \\ \end{matrix} \right|\]and\[10B=\left| \begin{matrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \\ \end{matrix} \right|\]. If\[B\]is the inverse of matrix\[A\], then\[\alpha \]is
A)
\[-1\]
done
clear
B)
\[-2\]
done
clear
C)
\[2\]
done
clear
D)
\[5\]
done
clear
View Answer play_arrow
question_answer 151) The angle of intersection of ellipse\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] and circle\[{{x}^{2}}+{{y}^{2}}=ab\]is
A)
\[{{\tan }^{-1}}\left( \frac{a+b}{ab} \right)\]
done
clear
B)
\[{{\tan }^{-1}}\left( \frac{a-b}{\sqrt{ab}} \right)\]
done
clear
C)
\[{{\tan }^{-1}}\left( \frac{a+b}{\sqrt{ab}} \right)\]
done
clear
D)
\[{{\tan }^{-1}}\left( \frac{a-b}{ab} \right)\]
done
clear
View Answer play_arrow
question_answer 152) If \[S=\sum\limits_{n=0}^{\infty }{\frac{{{(\log x)}^{2n}}}{(2n)!}}\], then\[S\]is equal to
A)
\[x+{{x}^{-1}}\]
done
clear
B)
\[x-{{x}^{-1}}\]
done
clear
C)
\[\frac{1}{2}(x+{{x}^{-1}})\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 153) The value of\[\log \,\,2+2\left( \frac{1}{5}+\frac{1}{3}\cdot \frac{1}{{{5}^{3}}}+\frac{1}{5}\cdot \frac{1}{{{5}^{5}}}+.... \right)\], is
A)
\[\log 2+\log 3\]
done
clear
B)
\[\log 2+2\]
done
clear
C)
\[\frac{1}{2}\log 2\]
done
clear
D)
\[\log 3\]
done
clear
View Answer play_arrow
question_answer 154) The equation of parabola whose vertex and focus are (0, 4) and (0, 2) respectively, is
A)
\[{{y}^{2}}-8x=32\]
done
clear
B)
\[{{y}^{2}}+8x=32\]
done
clear
C)
\[{{x}^{2}}+8y=32\]
done
clear
D)
\[{{x}^{2}}-8y=32\]
done
clear
View Answer play_arrow
question_answer 155) The line\[x+2y=4\]is translated parallel to itself by 3 unit in the sense of increasing x and then rotated by\[{{30}^{o}}\] in the anti-clockwise direction about the point where the shifted line cuts the x-axis. The equation of the line in the new position is
A)
\[y=\tan (\theta -{{30}^{o}})(x-4-3\sqrt{5})\]
done
clear
B)
\[y=\tan ({{30}^{o}}-\theta )(x-4-3\sqrt{5})\]
done
clear
C)
\[y=\tan (\theta +{{30}^{o}})(x+4+3\sqrt{5})\]
done
clear
D)
\[y=\tan (\theta -{{30}^{o}})(x+4+3\sqrt{5})\]
done
clear
View Answer play_arrow
question_answer 156) The distance between the foci of a hyperbola is double the distance between its vertices and the length of its conjugate axis is 6. The equation of the hyperbola referred to its axes as axes of coordinates are
A)
\[3{{x}^{2}}-{{y}^{2}}=3\]
done
clear
B)
\[{{x}^{2}}-3{{y}^{2}}=3\]
done
clear
C)
\[3{{x}^{2}}-{{y}^{2}}=9\]
done
clear
D)
\[{{x}^{2}}-3{{y}^{2}}=9\]
done
clear
View Answer play_arrow
question_answer 157) If the equation \[12{{x}^{2}}+7xy-p{{y}^{2}}-18x+qy+6=0\] represents a pair of perpendicular straight lines, then
A)
\[p=12,\,\,q=-1\]
done
clear
B)
\[p=-12,\,\,q=1\]
done
clear
C)
\[p=12,\,\,q=1\]
done
clear
D)
\[p=1,\,\,q=1\]
done
clear
View Answer play_arrow
question_answer 158) If the roots of the equation\[\frac{\alpha }{x-\alpha }+\frac{\beta }{x-\beta }=1\]be equal in magnitude but opposite in sign, then\[\alpha +\beta \]is equal to
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 159) If\[2a+3b+6c=0\], then at least one root of the equation\[a{{x}^{2}}+bx+c=0\]lies in the interval
A)
(1, 2)
done
clear
B)
(0, 1)
done
clear
C)
(2, 3)
done
clear
D)
(3, 4)
done
clear
View Answer play_arrow
question_answer 160) The ratio in which the line\[3x+4y+2=0\] divides the distance between\[3x+4y+5=0\] and\[3x+4y-5=0\], is
A)
\[7:3\]
done
clear
B)
\[3:7\]
done
clear
C)
\[2:3\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 161) If the circle\[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]is touched by\[y=x\]at\[P\]such that\[OP=6\sqrt{2}\], then the value of\[c\]is
A)
36
done
clear
B)
72
done
clear
C)
144
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 162) The coefficient of\[{{x}^{4}}\]in the expansion of\[{{(1+x+{{x}^{2}}+{{x}^{3}})}^{n}}\]
A)
\[^{n}{{C}_{4}}\]
done
clear
B)
\[^{n}{{C}_{4}}{{+}^{n}}{{C}_{2}}\]
done
clear
C)
\[^{n}{{C}_{4}}{{+}^{n}}{{C}_{2}}{{+}^{n}}{{C}_{4}}{{\cdot }^{n}}{{C}_{2}}\]
done
clear
D)
\[^{n}{{C}_{4}}{{+}^{n}}{{C}_{2}}{{+}^{n}}{{C}_{1}}{{\cdot }^{n}}{{C}_{2}}\]
done
clear
View Answer play_arrow
question_answer 163) \[1+\frac{1+x}{2!}+\frac{1+x+{{x}^{2}}}{3!}+\frac{1+x+{{x}^{2}}+{{x}^{3}}}{4!}\] is equal to
A)
\[\frac{{{e}^{x}}+1}{x-1}\]
done
clear
B)
\[\frac{{{e}^{x}}+1}{x+1}\]
done
clear
C)
\[\frac{{{e}^{x}}-e}{x+1}\]
done
clear
D)
\[\frac{{{e}^{x}}-e}{x-1}\]
done
clear
View Answer play_arrow
question_answer 164) The inequation\[n!>{{2}^{n-1}}\]is true for
A)
for all\[n\in N\]
done
clear
B)
for all\[n>1\]
done
clear
C)
for all\[n>2\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 165) Let\[A=\{(x,\,\,y):y={{e}^{x}},\,\,x\in R\}\]and\[B=\{(x,\,\,y):y={{e}^{-x}},\,\,e\in R\}\]. Then,
A)
\[A\cap B=\phi \]
done
clear
B)
\[A\cap B\ne \phi \]
done
clear
C)
\[A\cup B={{R}^{2}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 166) In\[\Delta \,ABC,\,\,\frac{b-c}{{{r}_{1}}}+\frac{c-a}{{{r}_{2}}}+\frac{a-b}{{{r}_{3}}}\]is equal to
A)
\[0\]
done
clear
B)
\[abc\]
done
clear
C)
\[a+b+c\]
done
clear
D)
\[ab+bc+ca\]
done
clear
View Answer play_arrow
question_answer 167) ABCD is a rectangular field. A vertical lamp post of height\[12\,\,m\]stands at the corner\[A\]. If the angle of elevation of its top from\[B\]is\[{{60}^{o}}\]and from\[C\]is \[{{45}^{o}}\], then the area of the field is
A)
\[48\sqrt{2}\,\,{{m}^{2}}\]
done
clear
B)
\[12\sqrt{2}\,\,{{m}^{2}}\]
done
clear
C)
\[48\,\,{{m}^{2}}\]
done
clear
D)
\[12\sqrt{3}\,\,{{m}^{2}}\]
done
clear
View Answer play_arrow
question_answer 168) The function\[f(x)=\max \{(1-x),\,\,(1+x),\,\,2\}\],\[x\in (-\infty ,\,\,\infty )\]is equivalent to
A)
\[f(x)=\left\{ \begin{matrix}
1+x & , & x\le -1 \\
2 & , & -1<x<1 \\
1-x & , & x\ge 1 \\
\end{matrix} \right.\]
done
clear
B)
\[f(x)=\left\{ \begin{matrix}
1-x & , & x\le -1 \\
2 & , & -1<x<1 \\
1+x & , & x\ge 1 \\
\end{matrix} \right.\]
done
clear
C)
\[f(x)=\left\{ \begin{matrix}
1-x & , & x\le -1 \\
1 & , & -1<x<1 \\
1+x & , & x\ge 1 \\
\end{matrix} \right.\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 169) The number of values of\[x\]in the interval\[[0,\,\,5\pi ]\]satisfying the equation\[3{{\sin }^{2}}x-7\sin x+2=0\]is
A)
0
done
clear
B)
5
done
clear
C)
6
done
clear
D)
10
done
clear
View Answer play_arrow
question_answer 170) \[\left( 1+\cos \frac{\pi }{8} \right)\left( 1+\cos \frac{3\pi }{8} \right)\left( 1+\cos \frac{5\pi }{8} \right)\]\[\left( 1+\cos \frac{7\pi }{8} \right)\]is equal to
A)
\[\frac{1}{2}\]
done
clear
B)
\[\frac{1}{8}\]
done
clear
C)
\[\cos \frac{\pi }{8}\]
done
clear
D)
\[\frac{1+\sqrt{2}}{2\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 171) The number of solutions of the equation\[2{{\sin }^{-1}}\sqrt{{{x}^{2}}-x-1}+{{\cos }^{-1}}\sqrt{{{x}^{2}}-x}=\frac{3\pi }{2}\]is
A)
0
done
clear
B)
2
done
clear
C)
4
done
clear
D)
\[\infty \]
done
clear
View Answer play_arrow
question_answer 172) Each side of a square subtends an angle of\[{{60}^{o}}\]at the top of a tower\[h\]metre high standing in the centre of the square. If a is the length of each side of the square, then
A)
\[2{{a}^{2}}={{h}^{2}}\]
done
clear
B)
\[2{{h}^{2}}={{a}^{2}}\]
done
clear
C)
\[3{{a}^{2}}=2{{h}^{2}}\]
done
clear
D)
\[2{{h}^{2}}=3{{a}^{2}}\]
done
clear
View Answer play_arrow
question_answer 173) The value of\[{{\cos }^{-1}}\left( \cos \frac{7\pi }{6} \right)\]is
A)
\[\frac{7\pi }{6}\]
done
clear
B)
\[\frac{5\pi }{6}\]
done
clear
C)
\[\frac{5\pi }{6}\]
done
clear
D)
\[\frac{13\pi }{6}\]
done
clear
View Answer play_arrow
question_answer 174) If\[n\in N\], then\[|\sin nx|\]
A)
\[\le n|\sin x|\]
done
clear
B)
\[\ge n|\sin x|\]
done
clear
C)
\[=n|\sin x|\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 175) In\[\Delta \,ABC\], if\[a=30,\,\,b=24,\,\,=18\], then\[{{r}_{3}}\]is equal to
A)
15
done
clear
B)
18
done
clear
C)
36
done
clear
D)
12
done
clear
View Answer play_arrow
question_answer 176) The circumcentre of a triangle formed by the lines\[xy+2x+2y+4=0\]and\[x+y+2=0\], is
A)
\[(0,\,\,-1)\]
done
clear
B)
\[(-1,\,\,0)\]
done
clear
C)
\[(1,\,\,1)\]
done
clear
D)
\[(-1,\,\,-1)\]
done
clear
View Answer play_arrow
question_answer 177) One diagonal of a square is along the line\[8x-15y=0\]and one of its vertex is (1, 2). Then, the equation of the sides of the square passing through this vertex are
A)
\[23x+7y=9,\,\,7x+23y=53\]
done
clear
B)
\[23x-7y-9=0,\,\,7x+23y-53=0\]
done
clear
C)
\[23x-7y+9=0,\,\,7x+23y+53=0\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 178) The two curves\[{{x}^{3}}-3x{{y}^{2}}+2=0\]and\[3{{x}^{2}}y-{{y}^{3}}=2\]
A)
cut at right angles
done
clear
B)
touch each other
done
clear
C)
cut at an angle\[\pi /3\]
done
clear
D)
cut at an angle\[\pi /4\]
done
clear
View Answer play_arrow
question_answer 179) If\[\frac{2x+3}{(x+1)(x-3)}=\frac{a}{x+1}+\frac{b}{x-3}\], then\[a+b\]is equal to
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[9/4\]
done
clear
D)
\[-1/4\]
done
clear
View Answer play_arrow
question_answer 180) \[\underset{n\to \infty }{\mathop{\lim }}\,\frac{1}{n}\left[ {{\sec }^{2}}\frac{\pi }{4n}+{{\sec }^{2}}\frac{2\pi }{4n}+...+{{\sec }^{2}}\frac{n\pi }{4n} \right]\]is equal to
A)
\[\frac{4}{\pi }\]
done
clear
B)
\[\frac{2}{\pi }\]
done
clear
C)
\[\frac{3}{\pi }\]
done
clear
D)
\[\frac{5}{\pi }\]
done
clear
View Answer play_arrow
question_answer 181) If\[f(x)=|\cos x|\]and\[g(x)=[x]\], then\[gof(x)\]is equal to
A)
\[|\cos [x]|\]
done
clear
B)
\[|\cos x|\]
done
clear
C)
\[[|\cos x|]\]
done
clear
D)
\[|[\cos x]|\]
done
clear
View Answer play_arrow
question_answer 182) If\[\underset{x\to \infty }{\mathop{\lim }}\,{{\left( 1+\frac{a}{x}+\frac{b}{{{x}^{2}}} \right)}^{2x}}={{e}^{2}}\],then
A)
\[a=1,\,\,b=2\]
done
clear
B)
\[a=2,\,\,b=1\]
done
clear
C)
\[a=1,\,\,b\in R\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 183) The area bounded by the curve\[{{y}^{2}}=2x+1\]and the straight line\[x-y-1=0\]is given by
A)
\[\frac{9}{2}sq\,\,units\]
done
clear
B)
\[\frac{43}{6}sq\,\,units\]
done
clear
C)
\[\frac{35}{6}sq\,\,units\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 184) The value of\[f(0)\], so that the function\[f(x)=\frac{2-{{(256-7x)}^{1/8}}}{{{(5x+3x)}^{1/5}}-2},\,\,x\ne 0\]is continuous everywhere is given by
A)
\[-1\]
done
clear
B)
\[1\]
done
clear
C)
\[{{2}^{6}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 185) The set of points where the function\[f(x)=x|x|\]is differentiable, is
A)
\[(-\infty ,\,\,\infty )\]
done
clear
B)
\[(-\infty ,\,\,0)\cup (0,\,\,\infty )\]
done
clear
C)
\[(0,\,\,\infty )\]
done
clear
D)
\[[0,\,\,\infty )\]
done
clear
View Answer play_arrow
question_answer 186) If\[f(x)=|x{{|}^{|\sin x|}}\], then\[f\left( -\frac{\pi }{4} \right)\]is equal to
A)
\[{{\left( \frac{\pi }{4} \right)}^{1/\sqrt{2}}}\left( \frac{\sqrt{2}}{2}\log \frac{4}{\pi }-\frac{2\sqrt{2}}{\pi } \right)\]
done
clear
B)
\[{{\left( \frac{\pi }{4} \right)}^{1/\sqrt{2}}}\left( \frac{\sqrt{2}}{2}\log \frac{4}{\pi }+\frac{2\sqrt{2}}{\pi } \right)\]
done
clear
C)
\[{{\left( \frac{\pi }{4} \right)}^{1/\sqrt{2}}}\left( \frac{\sqrt{2}}{2}\log \frac{\pi }{4}-\frac{2\sqrt{2}}{\pi } \right)\]
done
clear
D)
\[\left( \frac{\sqrt{2}}{2}\log \frac{\pi }{4}+\frac{2\sqrt{2}}{\pi } \right)\]
done
clear
View Answer play_arrow
question_answer 187) A circle touches the x-axis and also touches the circle which centre at (0, 3) and radius 2, The locus of the centre of the circle is
A)
a parabola
done
clear
B)
a circle
done
clear
C)
an ellipse
done
clear
D)
a hyperbola
done
clear
View Answer play_arrow
question_answer 188) The circle on focal radii of a parabola as diameter touches
A)
the x-axis
done
clear
B)
the tangent at the vertex
done
clear
C)
the directrix
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 189) The, equation of the ellipse whose axes are parallel to the coordinate axes having its centre at the point (2, -3) and focus at (3,-3) and one vertex at (4, -3) is
A)
\[\frac{{{(x-2)}^{2}}}{4}+\frac{{{(y+3)}^{2}}}{3}=1\]
done
clear
B)
\[\frac{{{(x+2)}^{2}}}{3}+\frac{{{(y+3)}^{2}}}{4}=1\]
done
clear
C)
\[\frac{{{(x+2)}^{2}}}{4}+\frac{{{(y+3)}^{2}}}{3}=1\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 190) The diameter of\[16{{x}^{2}}-9{{y}^{2}}=144\]which is conjugate to\[x=2y\]is
A)
\[y=\frac{32x}{9}\]
done
clear
B)
\[x=\frac{16}{9}y\]
done
clear
C)
\[y=\frac{16}{9}x\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 191) If\[\frac{2x+3}{(x+1)(x-3)}=\frac{a}{x+1}+\frac{b}{x-3}\]then\[a+b\]is equal to
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[9/4\]
done
clear
D)
\[-1/4\]
done
clear
View Answer play_arrow
question_answer 192) If\[\frac{{{e}^{x}}+2}{({{e}^{x}}-1)(2{{e}^{x}}-3)}=-\frac{3}{{{e}^{x}}-1}+\frac{B}{2{{e}^{x}}-3}\]then\[B\]is equal to
A)
1
done
clear
B)
3
done
clear
C)
5
done
clear
D)
7
done
clear
View Answer play_arrow
question_answer 193) \[\frac{3\sqrt{2}}{\sqrt{6}+\sqrt{3}}-\frac{4\sqrt{3}}{\sqrt{6}+\sqrt{2}}+\frac{\sqrt{6}}{\sqrt{3}+\sqrt{2}}\]equal to
A)
\[5\sqrt{2}\]
done
clear
B)
\[3\sqrt{2}\]
done
clear
C)
\[2\sqrt{3}\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 194) If\[{{\log }_{3}}2,\,\,{{\log }_{3}}({{2}^{x}}-5)\]and\[{{\log }_{3}}\left( {{2}^{x}}-\frac{7}{2} \right)\]are in AP, then\[x\]is equal to
A)
\[1,\,\,\frac{1}{2}\]
done
clear
B)
\[1,\,\,\frac{1}{3}\]
done
clear
C)
\[1,\,\,\frac{3}{2}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 195) If the roots of the cubic equation\[a{{x}^{3}}+b{{x}^{2}}+cx+d=0\]are in GP, then
A)
\[{{c}^{3}}a={{b}^{3}}d\]
done
clear
B)
\[c{{a}^{3}}=b{{d}^{3}}\]
done
clear
C)
\[{{a}^{3}}b={{c}^{3}}d\]
done
clear
D)
\[a{{b}^{3}}=c{{d}^{3}}\]
done
clear
View Answer play_arrow
question_answer 196) In the group\[G=(\{1,\,\,2,\,\,3,\,\,4\},\,\,{{\times }_{5}})\]the solution of\[{{2}^{-1}}\times (3{{\times }_{5}}x)=4\]is
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 197) Negation of Ram is in Class X or Rashmi is in Class XII is
A)
Ram is not in Class X but Rashmi is in Class XII
done
clear
B)
Ram is not in Class X but Rashmi is in Class XII
done
clear
C)
Either Ram is not in Class X or Rashmi is not in class XII
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 198) The inverse of the proportion\[(p\wedge \tilde{\ }q)\Rightarrow r\]is
A)
\[\tilde{\ }r\Rightarrow \tilde{\ }p\vee q\]
done
clear
B)
\[\tilde{\ }p\wedge q\Rightarrow \tilde{\ }r\]
done
clear
C)
\[r\Rightarrow p\vee \tilde{\ }q\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 199) The least remainder when \[{{17}^{30}}\] is divided by 5, is
A)
2
done
clear
B)
1
done
clear
C)
4
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 200) The solution of differential equation; \[dy-\sin x\,\sin \,ydx\,=0\] is
A)
\[{{e}^{\cos x}}\cdot \tan \frac{y}{2}=C\]
done
clear
B)
\[{{e}^{\cos x}}\cdot \tan y=C\]
done
clear
C)
\[\cos x\cdot \tan y=C\]
done
clear
D)
\[\cos x\cdot \sin y=C\]
done
clear
View Answer play_arrow
question_answer 201) Directions: Choose the alternative which can be substituted for the given group of words. A person concerned with practical results and values
A)
plagiarist
done
clear
B)
realist
done
clear
C)
pragmatist
done
clear
D)
fundamentalist
done
clear
View Answer play_arrow
question_answer 202) Directions: Choose the alternative which can be substituted for the given group of words. Member of a band of robbers
A)
dacoit
done
clear
B)
brigand
done
clear
C)
thief
done
clear
D)
pirate
done
clear
View Answer play_arrow
question_answer 203) Directions: Choose the alternative which can be substituted for the given group of words. A person without manners or polish is
A)
rustic
done
clear
B)
naïve
done
clear
C)
boorish
done
clear
D)
barbarian
done
clear
View Answer play_arrow
question_answer 204) Directions: Choose the alternative which can be substituted for the given group of words. A speech by an actor at the end of a play
A)
epilogue
done
clear
B)
monologue
done
clear
C)
duologue
done
clear
D)
prologue
done
clear
View Answer play_arrow
question_answer 205) Directions: Choose the most suitable alternative to fill in the blank. The teacher ordered Kamal to leave the room and ......... him to return.
A)
stopped
done
clear
B)
refused
done
clear
C)
forabade
done
clear
D)
challenged
done
clear
View Answer play_arrow
question_answer 206) Directions: Choose the most suitable alternative to fill in the blank. I hope you must have ......... by now that failures are the stepping stones to success.
A)
known
done
clear
B)
felt
done
clear
C)
decided
done
clear
D)
realized
done
clear
View Answer play_arrow
question_answer 207) Directions: Choose the most suitable alternative to fill in the blank. The tyrant......... anyone whom he regarded as a rival.
A)
massacred
done
clear
B)
killed
done
clear
C)
exterminated
done
clear
D)
slaughtered
done
clear
View Answer play_arrow
question_answer 208) Directions: Choose the most suitable alternative to fill in the blank. In a little publicized deal, Pepsi Cola has ......... the entire soft drink market in Afghanistan.
A)
conquered
done
clear
B)
swallowed
done
clear
C)
captured
done
clear
D)
occupied
done
clear
View Answer play_arrow
question_answer 209) Directions: Choose the alternative which is nearest in meaning to the word given in capital letters. DILETTANTE
A)
Opponent
done
clear
B)
Specialist
done
clear
C)
Amateur
done
clear
D)
Expert
done
clear
View Answer play_arrow
question_answer 210) Directions: Choose the alternative which is nearest in meaning to the word given in capital letters. FLAK
A)
Adventure
done
clear
B)
Advice
done
clear
C)
Criticism
done
clear
D)
Praise
done
clear
View Answer play_arrow
question_answer 211) Directions: Choose the alternative which is nearest in meaning to the word given in capital letters. HOODLUM
A)
Pioneer
done
clear
B)
Criminal
done
clear
C)
Devotee
done
clear
D)
Scholar
done
clear
View Answer play_arrow
question_answer 212) Directions: Choose the alternative which is nearest in meaning to the word given in capital letters. SPASMODIC
A)
Continuous
done
clear
B)
Gradual
done
clear
C)
Intermittent
done
clear
D)
Spontaneous
done
clear
View Answer play_arrow
question_answer 213) Directions: Choose the alternative which is opposite in meaning of the word given in capital letters. SHAME
A)
Glorify
done
clear
B)
Exalt
done
clear
C)
Dignify
done
clear
D)
Enshrine
done
clear
View Answer play_arrow
question_answer 214) Directions: Choose the alternative which is opposite in meaning of the word given in capital letters. RESCUE
A)
Extricate
done
clear
B)
Waver
done
clear
C)
Bind
done
clear
D)
Desert
done
clear
View Answer play_arrow
question_answer 215) Directions: Choose the alternative which is opposite in meaning of the word given in capital letters. AGONY
A)
Pleasure
done
clear
B)
Bliss
done
clear
C)
Ecstasy
done
clear
D)
Fear
done
clear
View Answer play_arrow
question_answer 216) Directions: Choose the alternative which is opposite in meaning of the word given in capital letters. REQUISITE
A)
Dispensable
done
clear
B)
Random
done
clear
C)
Inappropriate
done
clear
D)
Chaotic
done
clear
View Answer play_arrow
question_answer 217) Old habits die hardly.
A)
die much hardly
done
clear
B)
die hard
done
clear
C)
die too hard
done
clear
D)
No improvement
done
clear
View Answer play_arrow
question_answer 218) The teacher asked, Why you are late?
A)
Why you were late
done
clear
B)
Why late you are
done
clear
C)
Why are you late
done
clear
D)
No improvement
done
clear
View Answer play_arrow
question_answer 219) It is ten years since I have begun living here.
A)
begun
done
clear
B)
had begun
done
clear
C)
began
done
clear
D)
No improvement
done
clear
View Answer play_arrow
question_answer 220) The various practices and norms for banks transactions are laid down by the Reserve Bank of India.
A)
are laid up
done
clear
B)
are led down
done
clear
C)
are lead up
done
clear
D)
No improvement
done
clear
View Answer play_arrow
question_answer 221) Knot: Watt: Fathom
A)
The terms are connected with rope
done
clear
B)
They are units of measurement
done
clear
C)
The terms are used by sailors
done
clear
D)
The terms are used for installing electricity
done
clear
View Answer play_arrow
question_answer 222) Majlis : Diet: Knesset
A)
These are parliaments of countries
done
clear
B)
These are old names of certain countries
done
clear
C)
These are foreign languages
done
clear
D)
These are the names of foods eaten in different countries
done
clear
View Answer play_arrow
question_answer 223) Kanha : Periyar : Dachigam
A)
These are mountain peaks
done
clear
B)
These are famous lagoons
done
clear
C)
These are hill stations
done
clear
D)
These are animal sanctuaries
done
clear
View Answer play_arrow
question_answer 224) Stirrup : Anvil: Drum
A)
These are used by folk artists
done
clear
B)
The items are used by riders
done
clear
C)
They are parts of ear
done
clear
D)
These are musical instruments
done
clear
View Answer play_arrow
question_answer 225) Kennedy : Indira : Palme
A)
They were Prime Ministers
done
clear
B)
They were very popular among children
done
clear
C)
They were Presidents.
done
clear
D)
All of them were assassinated
done
clear
View Answer play_arrow
question_answer 226) Chair : Door : Stick
A)
Book : Pen : Notebook
done
clear
B)
Statue : Brick : Pitcher
done
clear
C)
Mason : Carpenter : Cobbler
done
clear
D)
Tomato : Potato : Brinjal
done
clear
View Answer play_arrow
question_answer 227) Music : Guitar : Performer
A)
Trick : Rope : Acrobat
done
clear
B)
Dance : Tune : Instrument
done
clear
C)
Food : Recipe : Cook
done
clear
D)
Patient: Medicine : Doctor
done
clear
View Answer play_arrow
question_answer 228) Hair : Brush : Wig
A)
Cement: Brick : Building
done
clear
B)
Paper : Pen : Pencil
done
clear
C)
Iron : Hammer: Axe
done
clear
D)
Bread : Butter : Milk
done
clear
View Answer play_arrow
question_answer 229) Village : City : Suburb
A)
Footpath : Road : Highway
done
clear
B)
Pillow : Quilt: Bed
done
clear
C)
Flowers : Garden : Park
done
clear
D)
Pen : Pencil: Colour
done
clear
View Answer play_arrow
question_answer 230) Smile : Laugh : Cry
A)
Frown : Anger : Temper
done
clear
B)
Sit: Sleep : Play
done
clear
C)
Touch : Catch : Release
done
clear
D)
Morning : Night: Day
done
clear
View Answer play_arrow
question_answer 231) Which river of India is called Vridha Ganga?
A)
Krishna
done
clear
B)
Godavari
done
clear
C)
Cauveri
done
clear
D)
Narmada
done
clear
View Answer play_arrow
question_answer 232) The capital of Tanzania is
A)
Nairobi
done
clear
B)
Lusaka
done
clear
C)
Kaupala
done
clear
D)
Dar-e-Salaam
done
clear
View Answer play_arrow
question_answer 233) During which decade did the population of India record a negative growth rate?
A)
1921-31
done
clear
B)
1911-21
done
clear
C)
1941-51
done
clear
D)
1931-41
done
clear
View Answer play_arrow
question_answer 234) Marx belonged to
A)
Germany
done
clear
B)
Holland
done
clear
C)
France
done
clear
D)
Britain
done
clear
View Answer play_arrow
question_answer 235) Who is the author of A River Sutra?
A)
VS Naipaul
done
clear
B)
Nirad C Chaudhri
done
clear
C)
Gita Mehta
done
clear
D)
Vikram Seth
done
clear
View Answer play_arrow
question_answer 236) Who is known as the Father of Indian Missile Technology?
A)
Dr UR Rao
done
clear
B)
Dr. APJ Abdul Kalam
done
clear
C)
Dr. Chidambaram
done
clear
D)
Dr. Homi Bhabha
done
clear
View Answer play_arrow
question_answer 237) The art and science of map making is called
A)
remote sensing
done
clear
B)
cartography
done
clear
C)
photogrammetry
done
clear
D)
mapping
done
clear
View Answer play_arrow
question_answer 238) WTO basically promotes
A)
financial support
done
clear
B)
global peace
done
clear
C)
unilateral trade
done
clear
D)
multilateral trade
done
clear
View Answer play_arrow
question_answer 239) The forest in Sunderban is called
A)
scrub jungle
done
clear
B)
mangrove
done
clear
C)
deciduous forest
done
clear
D)
tundra
done
clear
View Answer play_arrow
question_answer 240) Indian Standard Time relates to
A)
\[75.5{}^\circ \text{ }E\text{ }longitude\]
done
clear
B)
\[82.5{}^\circ \text{ }E\text{ }longitude\]
done
clear
C)
\[90.5{}^\circ \text{ }E\text{ }longitude\]
done
clear
D)
\[0{}^\circ \text{ }longitude\]
done
clear
View Answer play_arrow