Current Affairs 5th Class

Category : 5th Class

GEOMETRY

FUNDAMENTALS         

•                   In geometry, there are three basic terms point, line and plane.
•                   Point: A point does not have length, breadth and height. It is a mark of position and is represented by a dot.
•                   Line: A line normally refers to a straight line which extends indefinitely in both the directions. Thus, it has length but no breadth and no height.

Example: If you hold a thread taut between two hands, it represents part of a line.

•                  Plane: A plane has two dimensions, length and breadth, but no height.

Example: A piece of paper represents a plane, Top of a table represents plane, etc.

Passing through a point, an infinite number of lines can be drawn.

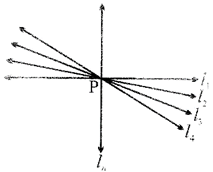
\[{{l}_{1,}}{{l}_{2.................}}{{l}_{n}}\] All pass through ?P?

These lines are also called CONCURRENT lines and the point P is called point of concurrence.

•                  Two lines in a place are either intersecting or parallel

      Collinearity of Points

Three points A, B, C in a place are collinear if they lie on the same straight line.

•                   One another way of testing collinearit6y of three points A, B and C is AB + BC = AC

If this equality holds, then points are collinear.

If this equality doesn?t hold, then points are non-collinear.

•                   Ray: Part of line which extends indefinitely from a given point ?P? is called a ray.

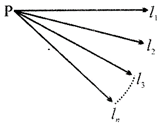
\[{{l}_{1,}}{{l}_{2,}}{{l}_{3..........}}{{l}_{n}}\]are all rays.

     Line Segment 

•                 Part of the line between two given points A and B on the line, is called a line segment.

•                 Line segment AB is represented as\[\overline{AB}\]. It is measured in ?cm? or ?inch?
•                Two line segments AB and CD are equal, they are of same length.

Example: if \[\overline{AB}\]=10cm and \[\overline{CD}=4\]inch then \[\overline{AB}=\overline{CD}\](because 1 inch=2.5 cm)

ANGLE

•                An angle is a figure formed by two rays with same initial point

Example:  

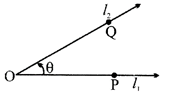
Rays \[{{l}_{1}}\] and \[{{l}_{2}}\] form an angle between them; this angle is represented as \[\theta =\angle POQ.\angle POQ\] can simply be written as\[\angle O\].

•                Unit of measurement of angle is degrees, which is represented as\[^{o}\]\[(eg:\,\,{{30}^{o}},\,\,{{60}^{o}},\,\,{{90}^{o}}\,\,etc)\]

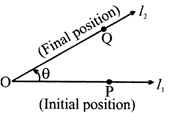
      Angles in a triangle

A plane figure bounded by three line segment is called a triangle. 

Example: 

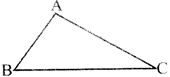
It has three angles \[\angle BAC\] (also called\[\angle A\]), \[\angle ABC\] (also called\[\angle B\]) and\[\angle ~ACB\] (also called\[\angle C\]).

•                 Sum of angles of\[\Delta \]is always\[{{180}^{o}}\].
•                 Right- angled \[\Delta \] or a right- angle\[\Delta \]:

In a\[\Delta \], if one angle \[={{90}^{o}}\]then it is called right angled triangle.

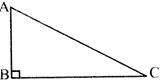
ABC is a right \[\Delta \] in which \[\angle B={{90}^{o}}\]

In a right-angle\[\Delta \], side opposite to right \[\angle \]is called hypotenuse. Other two sides are called base and perpendicular. The relation between these sides is given by Pythagoras as

\[{{\text{(Base)}}^{\text{2}}}\text{+(Perpendicular}{{\text{)}}^{\text{2}}}\text{=(Hypotenuse}{{\text{)}}^{\text{2}}}\]\[A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}\] (in right \[\Delta ABC\])

•                       Other types of \[\Delta \] are:

(i) Isosceles \[\Delta \](a \[\Delta \] in which two sides are equal)

(ii) Equilateral \[\Delta \](a \[\Delta \] in which all three sides are equal)

(iii) Scalene triangle \[\Delta \] (a \[\Delta \] in which no side is equal)

 If in \[\Delta \] ABC, AB=AC, then it is isosceles, also \[\angle \]B=\[\angle \]C

 If 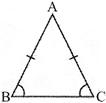 in equilateral\[\Delta ABC\],

\[AB=BC=CA\], also\[\angle A=\angle B=\angle C={{60}^{o}}\]

QUADRILATERALS

•                    A plane figure (meaning a figure drawn in a plane) bounded by four line segment is called a quadrilateral.

Type of Quadrilaterals are as follows:

(i) Trapezium: A quadrilateral having only one pair of parallel sides

(ii) Isosceles trapezium: It is a special type of trapezium in which non-parallel sides are equal i. e. \[AB||CD\] and\[AD=BC\]

(iii) Parallelogram: A quadrilateral having both pairs of opposite sides are parallel i. e.,\[AB||CD\]and\[AD||BC\]

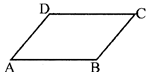
As a natural consequence of this, AB = CD and AD = BC, and \[\angle A=\angle C\]and\[\angle B=\angle D\]

(iv) Rhombus: It is a special type of parallelogram in which all side are equal

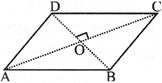
\[AB||CD\]

\[AD||BC\]

\[AB=BC=CD=DA\]

Also, \[\text{ A}C\bot BD\](i.e. diagonals are perpendicular to each other)

And,\[AO=CO\] and \[BO=DO\] (i.e., diagonals bisect each other)

•                   Rectangle: A parallelogram who?s each angle is right angle.

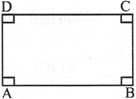
\[AB||CD;\,\,AD||BC\]

\[AB=CD;\,\,AD=BC\]

\[\angle A=\angle B=\angle C=\angle D={{90}^{o}}\]

•                   Square: A special type of rectangle whose all sides are equal.

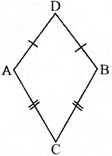
\[AB||CD;\,\,AD||BC\]

\[AB=BC=CD=DA\]

\[\angle A=\angle B=\angle C=\angle D={{90}^{o}}\]

•                   Kite: A quadrilateral which has equal adjacent sides but unequal opposite sides.

Adjacent Sides: \[AB=BC\] and\[AD=CD\]

Opposite sides: \[AB\ne CD\]; \[BC\ne AD\]

CIRCLE

•                    A circle is a set of points in a plane whose distance from a fixed point is constant

'O' is the fixed point called center.

'P' is movable point.

OP is called radius of a circle

•                   Diameter: A line segment passing through center and having its end points on the circle.

\[\therefore \] AB or CD are diameters.

Since infinite line segments can be drawn through O, therefore, numbers of diameters are infinite.

Now, look at the figure below:

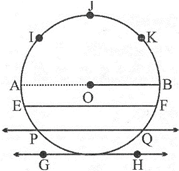
AB = diameter

•                 EF, which meets circle at two points is called chord of circle.
•                 Diameter is the largest chord.
•                Line through PQ where P and Q are points on circle, is called secant of a circle
•                 Line, (through GH) which touches circle at only one point is called Tangent to the circle.