
Identification of Terms of the Algebraic expression

Literals or Variables
Alphabetical symbols are used in mathematics called variables or literals, \[a,\text{ }b,\text{ }c,~~~d,\text{ }m,\text{ }n,\text{ }x,\text{ }y,\text{ }z\text{ }..........,\]etc. are some common letters used for variables.

Constant terms
The symbols which itself indicate a permanent value is called constant. All numbers are called constant. \[6,10,\frac{10}{11},15,-6,\sqrt{3}.......\]etc. are constant because, the value of the number does not change or remains unchanged. Therefore it is called constant.

Variable Terms
A term which contains various numerical values is called variable term. Product of 4 and\[\text{ }\!\!~\!\!\text{ X=4 }\!\!\times\!\!\text{ X=4X}\] Product of \[\text{2,X,}{{\text{Y}}^{\text{2}}}\]and \[Z=2\times X\times {{Y}^{2}}\times Z=2X{{Y}^{2}}\] Product of ?3, m and \[n=-3\times m\times n=-3mn\] Thus, \[4X,2X{{Y}^{2}}Z-3mn,\]are variable terms We also know that \[1\times X=X,1\times Y\times \text{ }z=YZ,-1\times {{a}^{2}}\times b\times c=-{{a}^{2}}\text{ }bc\]Thus\[\text{X,YZ,-}{{\text{a}}^{\text{2}}}\text{ bc}\]are variable terms

Types of Terms
There are two types of terms, like and unlike. Terms are classified by similarity of their variables.
Like Term The terms having same variables are called like terms. \[\text{6X, X,-2X, }\frac{\text{4}}{\text{9}}\text{X,}\], are like terms, \[\text{ab,-ab,4ab,9ab,}\]\[\text{ab},-\text{ab,4ab,9ab,}\] are like terms. \[\text{2}{{\text{X}}^{\text{2}}}\text{,3}{{\text{X}}^{\text{2}}}\text{Y,}{{\text{X}}^{\text{2}}}\text{Y,}\frac{\text{10}}{\text{7}}{{\text{X}}^{\text{2}}}\text{Y}\]are like terms.
Unlike Term The terms having different variables are called unlike terms. \[\text{6X, 2}{{\text{Y}}^{\text{2}}}\text{,}-\text{9}{{\text{X}}^{\text{2}}}\text{YZ, 4XY,}\]are unlike terms. \[\text{9a,}-\text{b,3}{{\text{a}}^{\text{2}}}\text{,4ab,}\]are unlike terms. \[\text{6}{{\text{X}}^{\text{2}}}\text{,7ab,4}{{\text{a}}^{\text{2}}}\text{b,}\]are unlike terms.

Coefficient
The coefficient of every term is multiplied with the term. In term, \[-6{{m}^{2}}\text{ }np,\]coefficient of\[-6=m{{n}^{2}}\]p because \[m{{n}^{2}}\text{ }p\]is multiplied with ? 6 to form \[\text{-- 6m}{{\text{n}}^{\text{2}}}\text{p}\] similarly. Coefficient of \[{{m}^{2}}=-6np,\]coefficient of \[n=-6{{m}^{2}}p\] Coefficient of \[{{\text{m}}^{\text{2}}}\text{n}\,\,\text{p=}-6\]and Coefficient of \[-6\text{=}{{\text{m}}^{\text{2}}}\text{np}\text{.}\]

Variable or Literal Coefficient
The variable part of the term is called its variable or literal coefficient. In term \[-\frac{\text{5}}{\text{4}}\text{abc,}\]variable coefficient is abc.

Constant Coefficient
The constant part of the term is called constant coefficient. In term \[-\frac{\text{5}}{\text{4}}\text{ }\!\!~\!\!\text{ abc,}\] constant coefficient is \[-\frac{\text{5}}{\text{4}}\text{ }\!\!~\!\!\text{ }\text{.}\]

Polynomials
An expression having two or more terms is known as polynomials. The expression \[3+5x\]is a polynomial and degree of the polynomial is the highest power of variable which presents in the term. In the expression, \[3+5x,x\]is the variable and its power is 1 therefore, the degree of the polynomial is 1.
\[5{{x}^{2}}+3{{y}^{3}}\](It is a polynomial in \[x\] and \[y\]and its degree is 3)
\[5{{x}^{2}}+3{{y}^{-3}}\] (It is not a polynomial as exponent if y is negative integer)
Monomials
An expression which has one term is called monomials, ie. \[4y,3{{b}^{2}}\]
Binomials
An expression which has two terms is called binomials, ie. \[3{{b}^{2}}-4ac.\]
Trinomials
An expression which has three terms is called trinomials, ie. \[{{x}^{2}}-ac+3z\]
Quadrinomials
An expression which has four terms is called Quadrinomials. ie.\[~{{a}^{2}}-bc+x-5\]
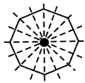
 If we fold these figures along an imaginary line, we will find that both the halves are mirror images of each other. The very common term used in our day to day life for these type of figures is "symmetry". So, symmetry occurs when one shape becomes exactly the same or both the figures overlap each other. Such types of figures are called symmetrical figures.
If we fold these figures along an imaginary line, we will find that both the halves are mirror images of each other. The very common term used in our day to day life for these type of figures is "symmetry". So, symmetry occurs when one shape becomes exactly the same or both the figures overlap each other. Such types of figures are called symmetrical figures. 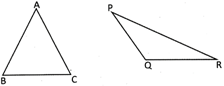 In ABC, \[\angle A+\angle B+\text{ }\angle C={{180}^{o}}\]
In APQR, \[\angle P+\angle Q+\angle R={{180}^{o}}\]
In ABC, \[\angle A+\angle B+\text{ }\angle C={{180}^{o}}\]
In APQR, \[\angle P+\angle Q+\angle R={{180}^{o}}\]
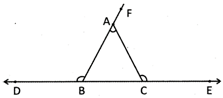 Thus,
\[\angle ACE=\angle BAC+\angle ABC\]
\[\angle ABD=\angle BAC+\angle ACB\]
\[\angle CAF=\angle ABC\text{ }+\angle ACB\]
Thus,
\[\angle ACE=\angle BAC+\angle ABC\]
\[\angle ABD=\angle BAC+\angle ACB\]
\[\angle CAF=\angle ABC\text{ }+\angle ACB\]
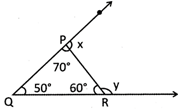 (a) \[x={{80}^{o}}\]and\[y={{10}^{o}}\]
(b) \[x={{110}^{o}}\]and\[~y={{120}^{o}}\]
(c) \[x={{70}^{o}}\]and\[y={{90}^{o}}\]
(d) All of these
(e) None of these
Answer: (b)
Explanation
\[x\]and\[y\] are the exterior angle therefore,
\[x=\angle PRQ\text{ }+\angle PQR={{60}^{o}}+{{50}^{o}}={{110}^{o}}\]
\[y=\angle QPR+\angle PQR={{70}^{o}}+{{50}^{o}}={{120}^{o}}\]
(a) \[x={{80}^{o}}\]and\[y={{10}^{o}}\]
(b) \[x={{110}^{o}}\]and\[~y={{120}^{o}}\]
(c) \[x={{70}^{o}}\]and\[y={{90}^{o}}\]
(d) All of these
(e) None of these
Answer: (b)
Explanation
\[x\]and\[y\] are the exterior angle therefore,
\[x=\angle PRQ\text{ }+\angle PQR={{60}^{o}}+{{50}^{o}}={{110}^{o}}\]
\[y=\angle QPR+\angle PQR={{70}^{o}}+{{50}^{o}}={{120}^{o}}\]