Current Affairs 8th Class

Category : 8th Class

FACTORS AND MULTIPLES

 

    FACTOR:

•             One Number is said to be a factor of another when it divides the other exactly.
•       If a number 'x' divides another number 'y' exactly, then we say that 'x' is a factor of 'y'.

 

Example:                16 = 1, 2, 4, 8, 16., so, 1, 2, 4, 8 and 16 are factors of 16.

25 = 1, 5, 25. so, 1,5 and 25 are factors of 25.

 

MULTIPLE:

•            A multiple of a number is a number obtained by multiplying it by integers.

or

•           If a number 'x' divides another number 'y' exactly, then we say that 'y' is a multiple of x.

 

Example:                5=5, 10, 15, 20.........and so on

\[5\times 1=5,\,\,\,5\times 2=10,5\times 3=15,5\times 4=20....................\]Thus,          

5, 10, 15, 20.....................are multiple of 5.

 

Properties of factors and multiples

•            Factors of a number is finite.
•            Multiples of a number is infinite.
•            Every number is a factor of itself.

 

Example:     \[1=1\times 1,\text{ }2=1\times 2,\text{ }5=1\times 5,\]and so on.

•            Every number is a multiple of itself.

 

Example:     \[2\times 1=2,\text{ }15\times 1=15,\text{ }18\times 1=18,\text{ }20\times 1=20\]and so on.

•           Every number is a factor of 0.

 

Example:       \[0=1,2,3,4,..........\left( \because \,\,\,\,\frac{0}{1}=0,\,\,\frac{0}{2}=0,\,\,\frac{0}{3}=....... \right)\]

•           0 is a multiple of every number.

\[0=1,2,3,4,..............(\because \,\,\,0\times 1=0,\,0\times 2=0,.....)\]

•             Every multiple of non-zero number is greater than or equal to that number.
•             Every factor of non - zero number is less than or equal to that number.

 

 

Some Number related to factors and multiple

•           Perfect Number: If the sum of all the divisors of the number is two times the number is called perfect number.

 

Example:          6 = 1, 2, 3, 6 the factors of 6 are 1, 2, 3 and 6.

Sum of all factors \[=1+2+3+6=12=2\times 6\]i.e., sum of all factors of \[6=2\times 6\]so, 6 is a perfect number.

Note: In 1 to 1000 there are three perfect numbers, 6, 28 and 496.

 

EVEN NUMBERS                                           

•            All multiples of 2 are called even numbers.

Here we know that 0, 2, 4, 6, 8, 10, 12, 14,...............are multiples of 2.

Question: Why zero is an even number?

Answer: check the first definition of "even", It is an integer multiple of 2, specifically\[0\times 2\].

 

ODD NUMBERS

•           Numbers which are not the multiples of 2 are called odd numbers.

 

Example: 1, 3, 5, 7, 9, 11, 13,.......... are odd numbers.

•           Numbers are either odd or even.
•           A number cannot be both even as well as odd.
•           In between 1 to 100, 50% of the numbers are odd or even.

 

PRIME AND COMPOSITE NUMBERS       

Prime Numbers

•           A number is greater than 1 having exactly two divisors 1 and the number itself is called prime number.
•           e.g,, 2, 3, 5, 7, 11, 13,.........are prime numbers.
•           2 is the only even prime number.
•           2 is the smallest prime number.
•           In between 1 to 100, there are 25 prime numbers.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

 

Composite Number                       

•           A number is greater than 3 and having more than 2 divisors is called a composite number.

or

•           A number having more than two factors is called a composite number.

 

Example: 6 = 1, 2, 3, 6 (1, 2, 3 and 6 are the factors of 6) 6 have more than two factors.

•           4 is the smallest composite number.

\[\therefore \]  4 = 1, 2, 4 (1, 2 and 4 are the factors of 4)

 

Example: 4, 6, 8, 9, 10, 12, 14, 15...........are composite numbers.

 

Some facts about factors 

•           How to find the number of factors of a composite number.

Let N denote the number, and consider

\[N={{a}^{p}}{{b}^{q}}{{c}^{r}}\]............... where a, b, c,..................

are different prime numbers and p, q, r,..................

are positive integers.

then no. of factors\[=(p+1)(q++1)(r+1)\]......................

 

Example: How many factors 48 have.

            \[48={{2}^{4}}={{3}^{1}}\]

2	48
2	24
2	12
2	6
	2

 

\[\therefore \]  No. of factors of \[48=(4+1)\times (1+1)=5\times 2=10\]

 

Example: 2 Find the no. of factors of 120.

Solution: \[120={{2}^{3}}\times {{3}^{1}}\times 5\]

                       

2	120
2	60
2	30
2	15
	5

 

\[\therefore \]  No. of factors of \[120=(3+1)\times (1+1)\times (1+1)=4\times 2\times 2=16\]

•           How to find the sum of the factors of a composite number.

Let N denote the number, and consider \[N={{a}^{p}}.{{b}^{p}}.{{c}^{r}}\].....................where a, b, c ................are different prime numbers and p, q, r ...are positive integers.

Then the required sum \[\frac{{{a}^{p+1}}-1}{a-1}.\frac{{{b}^{q+1}}-1}{b-1}.\frac{{{c}^{r+1}}-1}{c-1}............\]

 

Example: Find the sum of all the factors of 180.               

2	180
2	90
2	45
2	15
	5

 

Solution: \[180={{2}^{2}}\times {{3}^{2}}\times 5\]

The no. of factors \[=(2+1)(2+1)\times (1+1)\]\[=3\times 3\times 2=18\]

\[\therefore \]   Sum of the factors \[=\frac{{{2}^{2+1}}-1}{2-1}.\frac{{{3}^{2+1}}}{3-1}.\frac{{{5}^{1+1}}-1}{5-1}\]

                                    \[={{2}^{3}}-1\times \frac{{{3}^{3}}-1}{2}\times \frac{{{5}^{2}}-1}{4}\]

                                    \[=\frac{7\times 26\times 24}{8}=546\]

Twin - Primes

•           The pairs of prime numbers are said to be twin primes, if they differ by 2.

Example:     (3, 5), (5, 7) etc...

•            Pairs of twin prime between 1 to 100 are (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), and (71,73)

 

Prime Triplet;

•           The Triplet of prime numbers differ by 2, is called prime triplet.
•           The only prime triplet is (3, 5, 7).

 

Co - Prime:

•           Two numbers x and y are said to be co-prime, if 1 is the only common factor of x and y.

(2, 3), (3, 4), (5, 6), (8, 13), etc... are pairs of co-primes.

 

Prime Factorization

•           When a number is expressed as the product of prime numbers, it is called the prime factorization of the given number.

 

Example:   

2	50
5	25
5	5
	1

 

                        \[\therefore \,\,\,\,50=2\times 5\times 5\]

                       

2	180
2	90
3	45
3	15
5	5
	1

                        \[\therefore \,\,\,180=2\times 2\times 3\times 3\times 5\]

 

Highest common factor (H. C. F)

•           HCF of two or more numbers is the greatest number that divides each of them exactly.
•           HCF is also called GCD, GCF.

 

HCF by Prime factorization method

•           To find the HCF follows these Rules.
•           Express each of the number as the product of prime factors.
•           Then take out the common prime factors and multiply them.
•           That will be the HCF of given numbers.

 

Example:     Find the HCF of 20 and 25.

\[20=2\times 2\times 5\]

\[25=5\times 5\]

Common factor of 20 and 25 is 5.

Hence HCF of 20 and 25 is 5.

 

HCF by long division method

To find the HCF follows these Rules.

•           Divide the greater number by the smaller on then divide the divisor by the remainder.
•           Go on repenting the process of dividing the preceding divisor by the remainder, till zero remainder is obtained.
•           The last divisor is the required H.C.F. of the given numbers.

 

Example: 1   Find the HCF of 120 and 150.

Solution:

                       

\[\therefore \] HCF of 120 and 150 is 30.

 

Example: 2   Find the HCF of 120, 160 and 200.

                 

\[\therefore \]HCF of 120, 160 and 200 is 40.

Note:    (i) HCF of the distinct prime numbers is one.

(ii) HCF of two co-prime number is one.

(iii) HCF of an even number and an odd number is one.

(iv) HCF of two consecutive even number is two.

 

Least Common Multiple (LCM)       

•            The LCM of two or more given numbers is the least number which is exactly divisible by each of them.

LCM can be determined by three method.

1.     By writing the multiple of given number.

2.     By prime factorization method.

3.     By division method.

 

LCM by writing multiples of given number

•          Follows these steps.
•         Write the number.
•          Write the multiple of given number.
•          Round off all common multiples.
•          Compute the least common multiple from them.

Example:                Find the LCM of 5 and 15.

Solution:                Multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45...............

Multiples of 15 are 15, 30, 45, 60, 75, 90, 105...................

Common multiple of 5 and 15 are 30, 45.........................

Here the least common multiple of 5 and 15 is 30.

 

LCM by Prime factorization

Follows these steps

•           Resolve each of the given numbers into its prime factors and express the factors obtained in exponential form.
•           Find the product of the numbers having the highest powers of all the factors that occur in any of the given numbers.
•          The product obtained in step 2 is the required L.C.M.

 

Example: 1             Find the LCM of 20, 24.

Solution                 \[20=2\times 2\times 5,\text{ }24=2\times 2\times 2\times 3\]

                                    \[20={{2}^{2}}\times 5,\text{ }24={{2}^{3}}\times 3\]

Select the greater power of every factor.

LCM \[=23\times 3\times 5=120.\]

 

Example: 2             Find the LCM of 24, 36 and 40 by prime factorization method.

Solution                 \[24=2\times 2\times 2\times 3=23\times 3\]

\[36=2\times 2\times 3\times 3={{2}^{2}}\times {{3}^{2}}\]

\[40=2\times 2\times 2\times 5=23\times 51\]

\[\therefore \]  LCM of 24, 36, 40 is\[{{2}^{3}}\times {{5}^{1}}\times {{3}^{2}}=360\].

 

Example: 3             Find LCM of 32, 25, 100 by prime factorization method.

Solution                 \[32=25,\,\,25=52,\,\,100=22\times 52\]by taking maximum powers of prime factors.

\[\therefore \]      LCM\[=25\times 52=32\times 25=800\]

 

By Division method:

Follows these steps.

•           Write all the given numbers in a line separating them with a comma.
•           Find the prime number which divides at least two of the given numbers.
•           Repeat step - II and III until all the quotients are co-prime to each other.
•           Find the product of all prime divisors along with co-primes in the last column, this product is the LCM of the given numbers.

 

Example: 1       Find LCM of 30, 20, 60.

Solution:         

2	20, 30, 60
2	10, 15, 30
5	5, 15, 15
3	1, 3, 3
	1, 1, 1

 

LCM of 20, 30, 60 is\[2\times 2\times 5\times 3=60.\]

 

Example: 2   Find LCM of 24, 20 and 30 by division method.

Solution:

2	20, 24, 30
2	10, 12, 15
3	5, 6, 5
5	5, 2, 5
	1, 2, 1

 

LCM of 20, 24 and 30 is\[2\times 2\times 3\times 5\times 2=120.\]

Note:

•            If two numbers are relatively primes, then their LCM is equal to their product.
•            In the given two numbers if the first number is a multiple of second number, then their LCM is equal to the first number.
•            The least common multiple of two prime numbers is their product.
•            The LCM of two numbers is never less than either of the two numbers.

 

Relation between LCM and HCF

•            Product of two Numbers = LCM\[\times \]HCF

Let us take two number says 15 and 25 then,

HCF of 15 and 25 is 5.

LCM of 15 and 25 is 75.

Now, apply this relation

Product of numbers = LCM \[\times \] HCF

\[15\times 25=75\times 5\]

375 = 375

LHS = RHS

 

Example: The HCF and LCM of two numbers are 6 and 36 if one of the number is 12 then other number is.

Solution:          We know that,

Product of numbers = LCM \[\times \] HCF

\[12\,\,\times \]second number\[=36\times 6\]

Second number\[=\frac{36\times 6}{12}=18\]

\[\therefore \]   Second number = 18.

 

TEST OF DIVISIBILITY

•           A positive Integer N is divisible by
•           A natural number is divisible by 2 if and only if the digit in unit's place is even.

 

Example:          2540 is divisible by 2. (since units digit is 0)

5426 is divisible by 2. (since units digit is 6)

•           A natural number is divisible by 3 if and only if the sum of its digits is divisible by 3.

 

Example:          723 is divisible by 3.

(Since sum of 723 is 12 is divisible by 3).

•            A natural number is divisible by 4, if and only if the number formed by the last two digits is divisible by 4.

 

Example:          615 is not divisible by 4 (since 15 is not divisible by 4)

1248 is divisible by 4 (since 48 is divisible by 4)

•            A natural number is divisible by 5, if and only if the last digit is either 0 or 5.

 

Example:          24620 is divisible by 5.

76625 is divisible by 5.

•            A natural number is divisible by 6, if and only if, it is divisible by 2 and 3.

 

Example:          2070 is divisible by 6 (since 2070 is divisible by 2 and 3)

71232 is divisible by 6 (since 71232 is divisible by 2 and 3)

•          A natural number is divisible by 7, if and only if double the digit at the units place, then find the difference between the number obtained in previous step and the number formed by rest of its digits. Repeat this process until you find a number which is divisible by 7.

Example:          2401 is divisible by 7.

                                                 

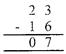
Hence 2401 is divisible by 7.

•            A natural number is divisible by 8 if and only if the number formed by the last three digits is divisible by 8.

 

Example: 12000, 20416. These both number are divisible by 8.

•           A natural number is divisible by 9 if and only if the sum of all digits is divisible by 9.

 

Example:     729, 65664 is divisible by 9, because the sum of the number is divisible by 9.

•           A natural number is divisible by 10 if and only if its units place is 0.

 

Example:      I860, 254670 etc.

•           A natural number is divisible by 11, if and only if the difference between the sum of digits in the odd places (starting from right) and sum of the digits in the even places (starting from the right) is a multiple of 11.

 

Example:     Consider the number 61809.

 (O denote odd place, E denote the even place)

\[\therefore \]Sum of its digit in odd place \[=6+8+9=23\]

\[\therefore \]Sum of its digit in even place\[=0+1=1\]

\[\therefore \]Difference of the two sum \[=23-1=22,\]

Which is divisible by 11.

Therefore, 61809 is divisible by 11.