2. Current Affairs
  3. Current Affairs
  4. 8th Class

Current Affairs 8th Class

Squares and Square roots

 Squares and Square Roots  
  • Square: The square of a number is the product obtained when a number is multiplied by itself.
 
  • Perfect Square: A perfect squares are the shares of whole numbers. Perfect squares are formed by multiplying a whole number by itself.
 
  • Properties of Squares:
(i) A number ending in 2, 3, 7 or 8 is never a perfect square. All square numbers end in 0, 1,4,5,6 or 9. (ii) A number ending in an odd number of zeroes is never a perfect square. (iii) Square numbers have only even number of zeros at the end. (iv) Squares of even numbers are even. (v) Squares of odd numbers are odd. (vi) For every natural number \[n,{{\left( n+1 \right)}^{2}}\text{ }-{{n}^{2}}=\left( n+1 \right)+\text{ }n.\] e.g.,\[{{9}^{2}}-{{8}^{2}}=9+8=17\]A triplet (a, b, c) of three natural numbers 'a; 'b' and 'c' is called a Pythagorean triplet If \[{{a}^{2}}+{{b}^{2}}={{c}^{2}}\] (viii) For any natural number m > 1, we have \[{{(2m)}^{2}}+{{({{m}^{2}}-1)}^{2}}=({{m}^{2}}+So,2m,({{m}^{2}}-1)\]and \[\left( {{m}^{2}}\text{ }+\text{ }1 \right)\]form a Pythagorean triplet. (ix) The square of a natural number 'n' is equal to the sum of the first 'n' odd numbers. (x) If a natural number cannot be expressed as a sum of successive odd natural numbers starting with 1, then it is not a perfect square,                                            
  • There are no natural numbers 'm' and 'n' for which \[{{m}^{2}}=2{{n}^{2}}.\]There are 2n non-perfect square numbers between the squares of the numbers n and (n + 1).
 
  • Square root: Square root is the inverse operation of square.
(i)  The square root of a number \['x'\] is a number which when multiplied by itself gives\['x'\] as the product. We denote the square root of \['x'\] by \[\sqrt{x}\] (ii) There are two integral square roots of a perfect square number. The positive square         root of a number is denoted by the symbol \[\sqrt{{}}\]   (iii) If x and y are positive numbers, work out the square root of the numerator and denominator separately.\[\sqrt{\frac{x}{y}}=\frac{\sqrt{x}}{\sqrt{y}}\] (vi)  Square root of a number can be found using the following methods. (a) Repeated subtraction    (b) Prime factorisation and    (c) Division  
  • Determining the square roots of positive numbers without using a calculator
(i) The square root of a fraction is determined by finding the square root of the numerator and denominator separately. (ii) Some fractions must be reduced to fractions with perfect squares as their numerators and denominators before their square roots can be calculated. (iii) To find the square root of a mixed number, first change the mixed number into an improper fraction. (iv) The square root certain decimals are obtained by first changing the decimals into fractions with perfect squares as their numerators and denominators.  
  • Estimating the number of digits in the square root of a given number: Place bars over every more...
Catgeory: 8th Class

Cubes and Cube roots

 Cubes and Cube Roots  
  • Cubes
(i) The cube of a number is the product of the number multiplied by itself twice. (ii) Write the cube of a number using the cube symbol or notation. (iii) \[{{8}^{3}}\]is read as 'eight cubed' or 'the cube of eight', or 'eight to the power of three.  
  • Estimating the cubes of numbers
Estimate the cube of a number by determining the range in which its value lies. e.g. Estimate the cube of 10.6 by determining the range in which its value lies.   Solution 10 < 10.6 < 11 \[\leftarrow \] Determine the range \[103<{{\left( 10.6 \right)}^{3}}<113\]\[\leftarrow \]Cube the range \[1000<{{\left( 10.6 \right)}^{3}}<1331\]Estimated answer \[\therefore {{\left( 10.6 \right)}^{3}}\]is between 1000 and 1331.  
  • Perfect cube
(i) A natural number is said to be a perfect cube if it is the cube of some natural number. (ii) Cubes of all even natural numbers are even. (iii) Cubes of all odd natural numbers are odd. (iv) Cubes of negative integers are negative.  
  • Cube roots of numbers
(i) The cube root of a number is a number which, when multiplied by itself twice, equals the given number. (ii) The symbol used for cube root is\[\sqrt{3}\] (iii) The cube root of a number  \['x'\] is that number whose cube gives\['x'\]. It is denoted as   (iv) For any positive integer \['x',\sqrt[3]{-x}=-\sqrt[3]{x}\] For any two integers 'a' and \['b'\] (a) \[\sqrt[3]{ab}=\sqrt[3]{a}\times \sqrt[3]{b}\]     (b)\[\sqrt[3]{\frac{a}{b}}=\frac{\sqrt{3}}{\sqrt{3}}\] (vi) Cube root of a number can be found by prime fatorisation.   Determining the cube roots (i) To find the cube roots of fractions, reduce the fractions to numerators and denominators that are cubes of integers. Then, find the cube roots of those integers. (ii) The find the cube roots of decimals, convert the decimals to fractions so that the numerators and denominators are cubes of integers. Then, solve the cube roots of those integers.  
Catgeory: 8th Class

Comparing Quantities

 Comparing Quantities  
  • Compound interest: Amount at compound interest is given by \[A=P{{\left( 1+\frac{R}{100} \right)}^{n}}\], where,
A - Amount,   P - Principal,    R - Rate of interest, n - Time period. (i) Compound interest = A - P (ii) In case of depreciation (or) decay, \[A=P{{\left( 1-\frac{R}{100} \right)}^{n}}\]
  • If the rates of increase in population P are p%, q% and r% during 1st, 2nd and 3rd years respectively, then the population after 3 years =
\[=P\left( \frac{P}{100} \right)\left( 1+\frac{q}{100} \right)\left( 1+\frac{r}{100} \right)\].  
  • If principal = R.s P, rate = R% per annum and time = n years, then
(a) Amount after 'n' years (compounded annually) is \[A=P{{\left( 1+\frac{R}{100} \right)}^{n}}\]   (b) Amount after 'n' years (compounded half-yearly) is \[A=P{{\left( 1+\frac{R}{2\times 100} \right)}^{2n}}\] where \[\frac{R}{2}\] is half-yearly rate and 2n is the number of half - years. (c) Amount after 'n' years (compounded quarterly) is   where\[\frac{R}{4}\] is the quarterly rate and 4n is the number of quarter years.   When T = 2 years and n = 1, then             CI.- S.I.= \[\frac{R\times S.I}{2\times 100}=P{{\left( \frac{R}{100} \right)}^{2}}\]   (v) When T = 3 years and n = 1, then \[C.I.-S.I=\frac{S.I.}{3}\left[ {{\left( \frac{R}{100} \right)}^{2}}+3\left( \frac{R}{100} \right) \right]\]
  • If a certain amount becomes N times in T years, then it will be
\[{{N}^{2}}\]times in T x 2 years, \[{{N}^{3}}\]times in T x 3 years and N" times in T x x years.  
  • Profit and loss:
(i) Cost price (C.P.): The price at which an article is purchased is called its cost price.   (ii) Selling price (S.P.): The price at which an article is sold is called its selling price.   (a) If S.P. > C.P., then there is a gain and Gain = S.P. - C.P. (b) If S.P. < C.P., then there is a loss and Loss = C.P. - S.P.  
  • Profit and loss percentage:
(i)\[~Profit%=\frac{~Profit%}{C.P.}\times 100%\]            (ii) \[Loss%=\left( \frac{loss%}{C.P.} \right)100%\]      Note: Profit and loss percentage are reckoned on cost price.                                  
  • Important formulae:
(a) \[S.P.=\left( \frac{100-gain%}{100}\times C.P. \right)\]  (b)\[S.P.=\left( \frac{100-loss%}{100}\times C.P. \right)\] (c)\[C.P.=\left( \frac{100}{100+gain%}\times S.P. \right)\] (d) \[C.P.=\left( \frac{100}{100+loss%}\times S.P. \right)\]  
  • Discount: In order to give a boost to the sales of an item or to clear the old stock, articles are sold at reduced prices. This reduction is given on the Marked Price (M.P.) of the article and is known as discount.
(a) S.P.= M.P.- Discount               (b) Discount = M.P. - S.P. (c)\[Discount\text{ }%=~\frac{M.P.-S.P.}{M.P.}\times 100\]       (d) Discount = Discount % of M.P. (e) Additional expenses made after buying an article are included in the cost price and are known as overhead expenses. C.P. more...
Catgeory: 8th Class

Algebraic Expressions and Identities

 Algebraic Expressions and Identities  
  • A combination of constants and variables connected by +, -, x and - is known as an algebraic expression.
e.g.,  \[2-3x+5{{x}^{-2}}{{y}^{-1}}+\frac{x}{3{{y}^{3}}}\]  
  • Polynomial:
An algebraic expression in which the variables involved have only non-negative integral powers is called a polynomial. e.g., \[2-3x+5{{x}^{2}}{{y}^{-1}}-\frac{x}{3}x{{y}^{3}}\]  
  • Like terms: Terms formed from the same variables whose powers are same are called like
terms. The coefficients of like terms need not be the same.  
  • Unlike terms: Terms formed from different variables whose powers may be same or different are called unlike terms. The coefficients of unlike terms may or may not be the same.
In other words, terms with the same variables and which have the same exponent are called like or similar terms, otherwise they are called unlike (or) dissimilar terms. e.g., (1)\[~3{{x}^{3}},\frac{1}{2}{{x}^{3}},- 9x3,.....\]  etc, are like terms. (2) \[{{\operatorname{x}}^{2}}y,3x{{y}^{2}},-4{{x}^{3}}, .....\] etc, are unlike terms.  
  • Degree of a polynomial:
 
  • In case of a polynomial in one variable, the highest power of the variable is called the degree of the polynomial.
e.g., \[5{{x}^{3}}-7x+\frac{3}{2}\]  is a polynomial in\['x'\]of degree 3.  
  • In case of polynomial in more than one variable, the sum of the powers of the variables in each term is taken up and the highest sum so obtained is called the degree of the polynomial.
  e.g., \[5{{x}^{3}}-2{{x}^{2}}{{y}^{2}}3{{x}^{2}}+9y\]  is a polynomial of degree 4 in \['x'\] and 'y'.  
  • Types of polynomials:
(i) Monomial: A polynomial containing 1 term is called a monomial.   (ii) Binomial: A polynomial containing 2 terms is called a binomial.   (iii) Trinomial: A polynomial containing 3 terms is called a trinomial.  
  • Multiplication of polynomials:
(i) A monomial multiplied by a monomial always gives a monomial. (ii) While multiplying a polynomial by monomial, we multiply every term in the polynomial by the monomial.   (iii) In carrying out the multiplication of a polynomial by a binomial (or trinomial), we multiply term by term, i.e., every term of the polynomial is multiplied by every term in the binomial (or trinomial). Note that in such multiplication, we may get terms in the product which are like and have to be combined.  
  • Identity:
 
  • An identity is an equality, which is true for all values of the variables in the equality.
 
  • Some important identities:
(i) \[{{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\] (ii)\[{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\] (iii) \[\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}\] (iv) \[\left( x+a \right)\left( x+b \right)={{x}^{2}}+\left( a+b \right)x+ab\]   (v) These identities are useful in computing squares and products of algebraic expressions. They are alternative methods to calculate products of numbers too.     more...
Catgeory: 8th Class

Visualising Solid Shapes

 Visualising Solid Shapes  
  • Geometrical shapes:
Plane shapes have two measurements - length and breadth and therefore they are called two-dimensional shapes. e.g.,   Solid objects have three measurements – length, breadth and height or depth. So, they are called three – dimensional shapes. Also, Solids Occupy some Space. e.g.,     ·                
  • Description of solid shapes:
 
S.NO. Solid Shape Number of Vertices Number of edges Number of faces
1. Cube 8 12 6
2. Cuboid 8 12 6
3. Cone 1 1 Curved edge 1 Curved face, 1 flat face
4. Cylinder Nil 2 Curved edges 2 flat face 1 Curved face
5. Sphere Nil Nil 1 Curved face
   
  • Polyhedron:
(i) A solid figure bounded by plane polygonal faces is called a polyhedron. (ii) The point at which three or more faces of a polyhedron intersect is called a vertex. (iii) A line along which two faces of a polyhedron intersect is called an edge.  
  • Regular polyhedron: A polyhedron with regular polygons as its faces is called a regular polyhedron. The same number of faces meet at each vertex.
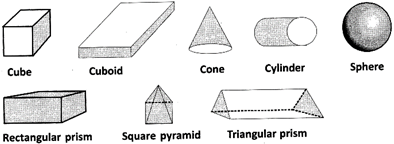
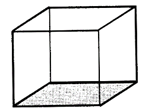    This polyhedron is regular. Its faces are congruent, regular polygons. Vertices are formed by the same number of faces.    
Catgeory: 8th Class

Mensuration

 Mensuration  
  • Perimeter: The length of the boundary of a plane figure is called its perimeter.
 
  • Area: The amount of surface enclosed by a plane figure is called its area.
 
  • Rectangle: Given a rectangle of length T units and breadth 'b' units,
  (i) Perimeter of the rectangle \[=2\left( l+b \right)\] units (ii) Diagonal of the rectangle,\[~d=\sqrt{{{l}^{2}}+{{b}^{2}}}\] units (iii) Area of the rectangle \[=\text{ }\left( \text{l}\times b \right)\]sq. units (iv)\[\operatorname{Length}=\left( \frac{area}{breadth} \right)units\] (v) \[\operatorname{Breadth}=\left( \frac{area}{length} \right)units\]  
  • Area of four walls of room: Let there be a room with length T units, breadth 'b' units and height 'h' units.
Then (i) Area of four walls \[=2\left( l+2 \right)\times h\]sq. units
  • (ii) Diagonal of room \[=\sqrt{{{l}^{2}}+{{b}^{2}}+}{{h}^{2}}\]units
 
  • Perimeter and area of a square: Let each side of a square be 'a' units. Then
(i) Perimeter of the square = (4a) units (ii) Diagonal of the square \[=\sqrt{{{a}^{2}}+{{a}^{2}}}=\sqrt{2a}=a\sqrt{2}\] Units. (iii) Area of the square \[={{a}^{2}}\]sq. units (iv) Area of the square \[=\frac{1}{2}\times {{\left( diagonal \right)}^{2}}\] sq. units (v) Side of the square \[=\sqrt{Area}\]units.  
  • Perimeter and area of a triangle:
(i) Let 'a', 'b' and 'c' be the lengths of sides of a triangle. Then, perimeter of the triangle is given by (a + b + c) units. \[s=\frac{1}{2}\left( a+b+c \right)\]is called semi-perimeter of the triangle.   (ii) Area of the triangle \[=\sqrt{s(s-a)(s-b)(s-c)}\] sq. units (iii) Let the base of a triangle be 'b' units and its corresponding height (or altitude) be 'h' units.  
  • Then the area of the triangle \[=\left( \frac{1}{2}\times b\times h \right)\]sq. units
Note:  We may consider any side of the triangle as its base. The the corresponding height would be the length perpendicular to this side from the opposite vertex.
  • (iv) Area of an equilateral triangle with each side 'a' units \[=\left( \frac{\sqrt{3}}{4}\times {{a}^{2}} \right)\]sq. Units.
(v) Height of an equilateral triangle of side 'a' units   \[\left( \frac{\sqrt{3}a}{2} \right)\]Units.
  • (vi) Area of a right triangle \[=\frac{1}{2}\times \](product of legs) sq. units
  Note: The sides containing the right angle are known as legs of a right triangle.  
  • Area of a parallelogram: Let ABCD be a parallelogram with base 'b' units and height 'h' units.
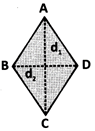
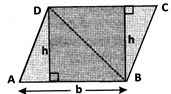    Then area of parallelogram = (base x height) sq. units  
  • Area of a rhombus: Let ABCD be a rhombus in which diagonal \[AC={{d}_{1}}\]units and diagonal \[BD={{d}_{2}}\]units.
more...
Catgeory: 8th Class

Exponents and Powers

 Exponents and Powers  
  • Exponential equation: An equation which has an unknown quantity as an exponent is called an exponential equation.
e.g.,      (i)\[{{5}^{x}}=625\] (ii) \[{{3}^{x-5}}=1\]   Note: If ax = ay, than x = y.  
  • Standard form of numbers: A number written in the form \[\left( m\times {{10}^{n}} \right)\]is said to be in standard form if 'm' is a decimal number between 1 and 9 and 'n' is either a positive or a negative integer.
Very large numbers and very small numbers are expressed in standard form.  
  • Laws of exponents (Integers): For any two non-zero integers 'a' and 'b', and any integers 'm' and 'n', the following laws hold good.
(i) \[{{a}^{m}}\times {{a}^{n}}={{a}^{m+n}}\]                  (ii)\[\frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m+n}}\left( m>n \right)\]             (iii) \[\frac{{{a}^{m}}}{{{a}^{n}}}=\frac{1}{{{a}^{m+n}}}\left( m<n \right)\]             (iv)\[\frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{0}}\left( m=n \right)\]             (v)\[{{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}\]             (vi)\[{{a}^{m}}\times {{b}^{m}}={{\left( ab \right)}^{m}}\]             (vii) \[\frac{{{a}^{m}}}{{{b}^{m}}}={{\left( \frac{a}{b} \right)}^{m}}\]             (viii) \[{{a}^{0}}=1\]  
  • Positive integral exponent of a rational number: For any rational number\[\frac{a}{b}\]and a positive integer\['n',{{\left( \frac{a}{b} \right)}^{n}}=\frac{{{a}^{n}}}{{{b}^{n}}}\].
     
  • Negative integral exponent of a rational number: For any rational number. \[\frac{a}{b}\] and a
positive integer \['n',{{\left( \frac{a}{b} \right)}^{-n}}={{\left( \frac{b}{a} \right)}^{n}}\].  
  • Zero exponent of a rational number: For any rational number\[\frac{a}{b}\]and '0',\[{{\left( \frac{a}{b} \right)}^{0}}=1\].
 
  • Special case of\[{{\mathbf{a}}^{\mathbf{n}}}\]:
\[{{a}^{n}}=1\]Only if n = 0 for any 'a' except a = 1 or a = -1. For a = 1, \[{{1}^{1}}={{1}^{2}}={{1}^{3}}={{1}^{-2}}=....=1\]or\[{{\left( 1 \right)}^{n}}=1\]for infinitely many \['n',\]
  • For a = - 1,
\[{{\left( -1 \right)}^{0}}={{\left( -1 \right)}^{2}}={{\left( -1 \right)}^{4}}={{\left( -1 \right)}^{-2}}=....=1\,or{{\left( -1 \right)}^{P}}=1\]for any even integer\['P',\] and \[{{(-1)}^{q}}=(-1)\] for any odd integer 'q'.  
  • Laws of exponents (Rational numbers): Let\[\frac{a}{b}\,and\,\frac{c}{d}\]be any two rational numbers, and 'm' and 'n' be any integers. Then,
\[{{\left( \frac{a}{b} \right)}^{m}}\times {{\left( \frac{a}{b} \right)}^{n}}={{\left( \frac{a}{b} \right)}^{m+n}}\] (ii) \[{{\left( \frac{a}{b} \right)}^{m}}+{{\left( \frac{a}{b} \right)}^{n}}={{\left( \frac{a}{b} \right)}^{m-n}}\] (iii) \[{{\left\{ {{\left( \frac{a}{b} \right)}^{m}} \right\}}^{n}}={{\left( \frac{a}{b} \right)}^{mn}}\] (iv) \[{{\left( \frac{a}{b}\times \frac{c}{d} \right)}^{n}}={{\left( \frac{a}{b} \right)}^{n}}\times {{\left( \frac{c}{d} \right)}^{n}}and\,{{\left\{ \frac{a/b}{c/d} \right\}}^{n}}=\frac{{{\left( a/b \right)}^{n}}}{{{\left( c/d \right)}^{n}}}\] (v) \[{{\left( \frac{a}{b} \right)}^{-n}}={{\left( \frac{b}{a} \right)}^{0}},\]When \['n'\]is a positive integer. (vi) \[{{\left( \frac{a}{b} \right)}^{0}}=1\]  
Catgeory: 8th Class

Direct and Inverse Proportions

 Direct and Inverse Proportions  
  • Unitary method:
A method in which the value of a quantity is first obtained to find the value of any required quantity is called unitary method.  
  • Direct proportion:
(i) Two quantities x and y are said to be in direct proportion if they increase (decrease) together in such a manner that the ratio of their corresponding values remains constant. (ii) That is, if \[\frac{X}{Y}=K\] [k is a positive number], then x and y are said to vary directly. In such
  • a case if \[{{\operatorname{y}}_{1}}\,and\,{{y}_{2}}\] are the values of y corresponding to the values \[{{\operatorname{x}}_{1\,}}\,and\,{{x}_{2}}\]of z respectively then \[\frac{{{x}_{1}}}{{{y}_{1}}}=\frac{{{x}_{2}}}{{{y}_{2}}},\]
 
  • Examples:
(a) As the number of articles increases, their cost increases. Cost is directly proportional to the number of articles. (b) The more the number of men, the more work is done in a given time. Work done is directly proportional to the number of men working at it.  
  • Inverse proportion:
(i) Two quantities x and y are said to be in inverse proportion if an increase in x causes a proportional decrease in y (and vice-versa) in such a manner that the product of their corresponding values remains constant. (ii) That is, if xy = k, then x and y are said to vary inversely. In this case, if \[{{\operatorname{y}}_{1}}\,and\,{{y}_{2}}\]are  
  • the values of y corresponding to the values \[{{\operatorname{x}}_{1}}\,and\,{{x}_{2}}\]of x respectively then
\[{{\operatorname{x}}_{1}}{{y}_{1}}={{x}_{2}}{{y}_{2}}\,or\,\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{y}_{2}}}{{{y}_{1}}}\].  
  • Examples:
(i) The more men employed, the less time it takes to complete a given work. The time taken to finish a work is inversely proportional to the number of persons working at it. (ii) If speed of car is increased, time taken to cover a given distance decreases. The time taken by any vehicle in covering a certain distance is inversely proportional to the speed of the vehicle.    
Catgeory: 8th Class

Factorisation

 Factorisation  
  • Factorisation:
(i) The process of writing an algebraic expression as the product of two or more algebraic expressions is called factorisation. (ii) When we factories an expression, we write it as a product of factors. These factors may be numbers, algebraic variables or algebraic expressions. (iii) An irreducible factor is that which cannot be expressed further as a product of factors. (iv) A systematic way of factorising an expression is the common factor method. It consists of three steps: (a) Write each term of the expression as a product of irreducible factors. (b) Look for and separate the common factors and (c) Combine the remaining factors in each term in accordance with the distributive law. (v) Sometimes, all the terms in a given expression do not have a common factor; but the terms can be grouped in such a way that all the terms in each group have a common factor. When we do this, there emerges a common factor across all the groups leading to the required factorisation of the expression. This is the method of regrouping.  
  • Some important identities:
A number of expressions to be factorised are of the form or can be put into the form: \[{{a}^{2}}+2ab+{{b}^{2}},\text{ }{{a}^{2}}-2ab\text{ }+{{b}^{2}},{{a}^{2}}-{{b}^{2}}and\text{ }{{x}^{2}}+\left( a+b \right)+ab.\]These expressions can be easily factorised using identities I, II, III and IV.
  • \[\,{{(a+b)}^{2}}\equiv {{a}^{2}}+2ab+{{b}^{2}}\]
  • \[\,{{(a-b)}^{2}}\equiv {{a}^{2}}-2ab+{{b}^{2}}\]
    • III. \[\left( a+b \right)\left( a-b \right)\equiv {{a}^{2}}-{{b}^{2}}\]
  • \[\left( x+a \right)\left( x-b \right)\equiv {{x}^{2}}+\left( a+b \right)x-ab\]
    •  
    • In expressions which have factors of the type (x + a) (x + b), remember that the numerical term gives ab. Its factors, a and b, should be so chosen that their sum, with signs taken care of, is the coefficient of x.
     
    • We know that in the case of numbers, division is the inverse of multiplication. This idea is applicable also to the division of algebraic expressions.
     
    Catgeory: 8th Class

    Introduction to Graphs

      Introduction to Graphs  
    • Bar graph: A bar graph is used to show comparison among categories.
     
    • Pie graph: A pie graph is used to compare parts of whole.
     
    • Histogram: Representation that shows data in intervals.
     
    • Line graph: It shows data that changes continuously over periods of time.
     
    • Linear graph: A straight line graph is called a linear graph.
     
    • The Cartesian system:
    (i)A plane is divided into 4 quarters (called quadrants) by two perpendicular lines, intersecting at 0 (called origin). The horizontal line is called the X-axis and the vertical line is called the Y-axis. (ii) A point is represented by the horizontal distance from the origin called the x-coordinate and by the vertical distance from the origin called the y-coordinate. (ii) A point is represented by an ordered pair (x, y) where x is the x-coordinate and y is the y-coordinate.
    • A graph shows the relation between two variables, one of which is an independent variable (or control variable) and the other a dependent variable.
     
    • Advantages and disadvantages of various graphs:
                
    Representation of data Advantages Disadvantages
    Pictogram Sales of Fruits Key:1 Represents 50 Apples Data is  represented in an attractive manner.        Not accurate Difficult and time more...
    Catgeory: 8th Class

    Current Affairs Categories


    Archive


    Trending Current Affairs

    You need to login to perform this action.
    You will be redirected in 3 sec spinner