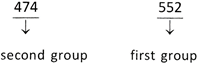Category :
8th Class
Number System
Learning Objectives
- Properties of Rational Numbers
- Square and Square Roots
- Cube and Cube Roots
- Playing with Numbers
- Divisibility Test
Properties of Rational Numbers
Rational numbers are the numbers that can be expressed in the form \[\frac{p}{q}\], where p and q are integers and \[q\ne ~0\] . The collection of rational numbers is denoted by Q. These rational numbers satisfy following laws or properties
- Rational numbers are closed under addition, subtraction and multiplication. If a, b are any two rational numbers, then the sum, difference and product of these rational numbers is also a rational number, thus we can say that rational numbers satisfy the closure law.
- Rational numbers are commutative under addition and multiplication. If a, b are rational numbers, then:
- Commutative law under addition: \[\mathbf{a}+\mathbf{b}=\mathbf{b}+\mathbf{a}\]
- Commutative law under multiplication: \[\mathbf{a}\times \mathbf{b}=\mathbf{b}\times \mathbf{a}\]
- Rational numbers are associative under addition and multiplication. If a, b, c are rational numbers, then:
- Associative law under addition: \[\mathbf{a}+\left( \mathbf{b}+\mathbf{c} \right)=\left( \mathbf{a}+\mathbf{b} \right)+\mathbf{c}\]
- Associative law under multiplication: \[\mathbf{a}\left( \mathbf{bc} \right)=\left( \mathbf{ab} \right)\mathbf{c}\]
- 0 is the additive identity for rational numbers.
- 1 is the multiplicative identity for rational numbers.
- The additive inverse of a rational number \[\frac{p}{q}\] is \[\left( -\frac{p}{q} \right)\], and the additive inverse of \[\left( -\frac{p}{q} \right)\] is\[\frac{p}{q}\].
- If \[\frac{a}{b}\times \frac{p}{q}=1\], then \[\frac{a}{b}\] is the reciprocal or multiplicative inverse of \[\frac{p}{q}\] and vice versa.
- For all rational numbers p, q and r; p (q + r) = pq + pr and p (q - r) = pq - pr is known as the distributive property.
Example
1. Find the multiplicative identity of the rational number \[\frac{\mathbf{455}}{\mathbf{1024}}\]
(a) \[\frac{1024}{455}\] (b) \[\frac{1}{455}\]
(c) \[\frac{1}{1024}\] (d) 1
(e) None of these
Answer: (a)
2. Which one of the following rational numbers lies between \[\frac{\mathbf{45}}{\mathbf{78}}\] and \[\frac{\mathbf{26}}{\mathbf{52}}\]?
(a) \[\frac{75}{156}\] (b) \[\frac{84}{156}\]
(c) \[\frac{95}{156}\] (d) \[\frac{105}{156}\]
(e) None of these
Answer: (b)
Explanation: On equating the denominator, the given rational number reduce to \[\frac{90}{156}\] and \[\frac{78}{156}\] and the rational number lying between these two is \[\frac{84}{156}\].
Square and Square Roots
If a natural number m can be expressed as \[{{n}^{2}}\], where n is also a natural number, then m is called the square root of a square number, \[{{n}^{2}}\]. For example, 1, 4, 9, 16, 25 are the square numbers. Some interesting properties of square numbers are as follows:
- All square numbers end with 0, 1, 4, 5, 6 or 9 at unit's place.
- No square number ends with 2, 3, 7 or 8 at unit's place.
- When a square number ends with 6 at unit's place, the number whose square it is, will have either 4 or 6 in unit's place.
- There are 2n non perfect square numbers between the squares of the numbers n and (n + 1).
- If a natural number cannot be expressed as a sum of successive odd natural numbers starting with 1, then it is not a perfect square.
- The square of any odd number is the sum of two consecutive positive integers.
If three numbers a, b and c are such that \[{{a}^{2}}+{{b}^{2}}+{{c}^{2}}\], then a, b and c are called as Pythagorean triplets. Square root is the inverse operation of square. Square root of a number can be find out by long division method or by the prime factorisation method. There are two integral square roots of a perfect square number.
Positive square root of a number is denoted by the symbol \[\sqrt{{}}\]. For example, \[{{3}^{2}}~=9,\] gives \[\sqrt{9}=3\].
Example
1. Find the value of 'y' such that \[\sqrt{\mathbf{188+}\sqrt{\mathbf{53+}\sqrt{\mathbf{y}}}\mathbf{=14}}\].
(a) 121 (b) 11
(c) 1331 (d) 161
(e) None of these
Answer: (a)
2. Simplify : \[\sqrt{\frac{\mathbf{1183}}{\mathbf{2023}}}\]
(a) \[\frac{17}{13}\] (b) \[\frac{1}{13}\]
(c) \[\frac{13}{17}\] (d) \[\frac{1}{17}\]
(e) \[7\sqrt{2}\]
Answer: (c)
Explanation: \[\sqrt{\frac{1183}{2023}}=\sqrt{\frac{13\times 13\times 7}{17\times 17\times 7}}=\frac{13}{17}\]
Cube and Cube Roots
- If a natural number m can be expressed as \[{{n}^{3}}\], where n is also a natural number, then m is called the cube root of a cube number, \[{{n}^{3}}\]. For example, 1, 8, 27, 64, 125 are the cubes.
- The number that can be expressed as a sum of two cubes in two different ways is called as Hardy - Ramanujan Number. 1729 is the smallest Hardy-Ramanujan Number. It can be expressed as sum of the cubes of 1, 12 and 9, 10.
Cube root is the inverse of cube. The symbol \[\sqrt[3]{{}}\] denotes 'cube-root?.
- There are two methods to find the cube root of a number - (i) Prime factorisation method and (ii) Estimation method.
- Prime factorisation method to find the cube root
\[21952=\underline{7\times 7\times 7}\times \underline{2\times 2\times 2}\times \underline{2\times 2\times 2}={{7}^{3}}\times {{2}^{3}}\times {{2}^{3}}\]
Therefore, \[\sqrt[3]{21952}=7\times 2\times 2=28\]
- Estimation method to find the cube root
Step 1: Take any cube number say 474552 and start making groups of three digits starting from the right most digit of the number.
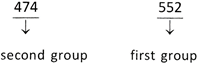
Step 2: First group, i.e., 552 will give you the ones (or units) digit of the required cube root. The number 552 ends with 2. We known that 2 comes at the unit's place of a number only when it's cube root ends with 8.
So, we get 8 at the unit's place of the cube root.
Step 3: Now take another group, i.e., 474.
We know that \[{{7}^{3}}=343\] and \[{{8}^{3}}=512\]. Also, \[343<474<512.\] We take the one's place, of the smaller number i.e., 7 as the ten's place of the required cube root. So we get \[\sqrt[3]{474552}=78\]
Example
1. Find the least number by which 3087 must be multiplied to make it a perfect cube.
(a) 3 (b) 4
(c) 9 (d) 7
(e) None of these
Answer: (a)
Explanation: The factors of \[3087=3\times 3\times 7\times 7\times 7\]
We note that the factor 3 appears only 2 times, so if we multiply 3087 by 3 we get \[3087\times 3={{\left( 3 \right)}^{3}}\times {{\left( 7 \right)}^{3}}={{\left( 3\times 7 \right)}^{3}}\], so the smallest number is 3 which when multiplied to 3087, it gives a perfect cube.
Playing With Numbers
Let's study some very interesting properties of numbers.
- When a two digit number is added into the number obtained by reversing its digits, the resulting total will be divisible by 11. But the resulting total in this case should not exceed 198.
- A number will be divisible by 11 if the difference between the sum of digits at its odd places and that of digits at the even places is divisible by 11.
- The difference between a two digit number and the number obtained by reversing its digit, is divisible by 9.
- The difference between a three digit number and the number obtained by reversing its digits, is divisible by 99.
- If a three digit number (abc) is added to the numbers obtained by shifting the ones digit of original number to hundreds place (cab) and the number obtained by shifting the ones digit of the changed number to hundreds place (bca), the resulting number (abc + cab + bca) will be divisible by 37. For example, if a number 452 is considered, then adding 452 to the numbers 245 and 524 gives 1221 which on dividing by 37 gives 33.
Divisibility Tests
- Divisibility by 2: All even numbers i.e. all numbers ending in 0, 2, 4, 6 or 8 are divisible by 2.
- Divisibility by 3: If on adding up all the digits in the number gives a sum which is divisible by 3, then the given number is also divisible by 3. For example, the sum of all digits of 12123 is 9 (1 + 2 + 1 + 2 + 3 = 9) which is divisible by 3, then the number 12123 is also divisible by 3.
- Divisibility by 4: If the last two digits in the number are divisible by 4, then the given number is also divisible by 4. For example, 358912 end in 12 which is divisible by 4, thus 358912 is divisible by 4.
- Divisibility by 5: The numbers ending in a 5 or a 0 are always divisible by 5.
- Divisibility by 6: If the Number is divisible by 2 and 3, it is divisible by 6 also.
- Divisibility by 8: If the last 3 digits are divisible by 8, so is the entire number. For example, the last 3 digits of 6008 are divisible by 8, therefore 6008 is also divisible by 8.
- Divisibility by 9: Add up all the digits in the number. If the sum is divisible by 9, then the given number is also divisible by 9. For example, in case of 43785 the sum of digits (4 + 3 + 7 + 8 + 5 = 27) is 27 which is divisible by 9, therefore 43785 is also divisible by 9.
- Divisibility by 10: If the number ends in a 0, it is divisible by 10.
Example
1. Find the value of P if 7654P321 is divisible by 9.
(a) 2 (b) 7
(c) 8 (d) 9
(e) None of these
Answer: (a)
Explanation: For the given number 7654P321 to be divisible by 9, the sum of its digits should be equal to 9 or any of its multiple, i.e.,
7 + 6 + 5 + 4 + P + 3 + 2 + 1 = 28 + P.
Thus, for 28 + P to be divisible by 9, it should be equal to 36. (Here P cannot be negative).
Hence, 28 + P = 36 or P = 8.