Fluid Mechanics and Machinery
Fluid: Fluid is a substance which has the property tendency to flow under the action of shear and tangential forces.
Liquids and gases both are fluids.
Ideal and Real fluids:
- In ideal fluids, there is no viscosity and no surface tension and are incompressible.
- In real fluids, viscosity, surface tension together exist and are compressible along with density.
Classification of fluids:
Fluids can be classified on the basis of the following:
Based on density and viscosity
(i) Ideal fluid: An ideal fluid is described as a fluid which is in compressible and also has zero viscosity and constant density.
(ii) Real fluids: A real fluid is described as a fluid which is compressible and viscous by nature. The density of real fluid are variable and while in motion, an amount of resistance is always offered by these fluids.
(iii) Newtonian fluids: Newtonian fluidss are denned as fluids those obey Newton's law of viscosity. The density of these fluids may be constant or variable. The viscosity is calculated according to Newton'.s law of viscosity as:
\[\tau =\mu \frac{du}{dy}\]
where, \[\tau \]=shear stress
\[\mu =\]viscosity of fluid
\[du/dy=\]velocity gradient
Examples are, water, ethyl alcohol, benzene etc.
(iv) Non – Newtonion fluids: Non-newtonian fluids are defined as fluids those do not obey Newton's laws of viscosity.
The density of these fluids may be constant or variable and the viscosity of these fluids does not remain constant.
Examples are Gels, Solutions of polymers, pastes etc.
(v) Compressible fluids: A compressible fluid is defined as the fluid which reduces its volume when an external pressure is applied. All the fluids available in nature are compressible.
(vi) In–compressible fluids: Incompressible fluids are defined as the fluids whose density does not change when the value of pressure changes. There is no effect of pressure on the density of fluid. In these fluids, density remains constant and viscosity remains non-zero.
(vii) Inviscid fluid: Inviscid fluid is the fluid which has zero iscosity and density may be constant or variable.
FLUID PROPERTIES
Density\[(\rho )\]: It is denned as mass per unit volume of substance.
\[\rho =\frac{m}{V}\]
Specific Weight\[(\omega )\]: It is defined as weight per unit volume of substance.
\[\omega =\frac{mg}{V}=\rho g\]
Relative density Specific gravity (Sg): It is defined as ratio of density of fluid to the density of standard fluid.
It may also be defined as the ratio of specific weight of the fluid to the standard weight of fluid.
\[\text{Sg=}\frac{\text{weogjt}\,\,\text{of}\,\,\text{fluid}}{\text{weight}\,\,\text{of}\,\,\text{standard}\,\,\text{fluid}}\]
\[\text{Sg=}\frac{\text{Density}\,\,\text{of}\,\,\text{fluid}}{\text{Density}\,\,\text{of}\,\,\text{standard}\,\,\text{Fluid}}\]
Ex: oil of Sg of 0.8\[\Rightarrow {{\rho }_{oil}}=800\,\,kg/{{m}^{3}}\]
Specific volume (v):
It is expressed as the volume per unit mass of fluid.
\[v=\frac{V}{m}=\frac{1}{\rho }\]
Compressibility \[(\beta )\]
Hydrostatic law: It states that rate of increase of pressure in a vertical direction is equal to weight density of fluid at that point.
Mathematically, pressure head (h)\[(h)=\frac{\rho }{\rho g}\]
\[\beta =\frac{-\frac{dV}{V}}{dp}=\frac{1}{\rho }\,\,\frac{d\rho }{dp}\]
Liquids are highly incompressible.\[\therefore \,\frac{d\rho }{dp}=0\]
Gases are highly compressible as \[P\propto \rho
more...
Fig.: PN Junction Diode
Modes of Operation
There are generally two types of modes of operation for diodes:
(i) Forward Bias: When an external voltage source is applied to one end of the junction in such a manner that it overcomes the potential barrier and permits current to flow, it is called Forward Biasing.
In case of a PN junction Diode, in order to operate the diode in the forward biasing mode, the p-type semiconductor (anode) is connected to the positive terminal, while the n-type semiconductor (cathode) is connected to the negative terminal of an external voltage source as shown in the fig.
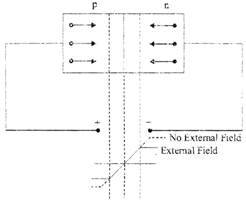Fig.: Forward Biasing
(ii) Reverse Bias: This acts opposite to the forward biasing mode i.e. in this mode an external voltage source is connected in such a manner, that it will increase the potential barrier and resist the flow of current, m this mode the p-type semiconductor (anode) is connected to the negative terminal and the n-type semiconductor (cathode) is connected to the positive terminal as shown in fig.
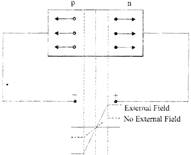Fig.: Reverse Biasing
V-I Characteristics
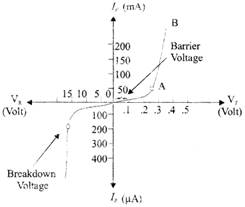Fig.: V-I Characteristics
Effect of Temperature on Diode Characteristic
In the last section, we had discussed about diode current equation, in which it is clearly mentioned that diode current is a function of temperature and since the coefficient of temperature\[\left( {{V}_{T}} \right)\]is in the denominator of the power of the exponential term:
\[I={{I}_{0}}({{e}^{V/{{\eta }^{V}}T-1}})\]
therefore, with an increase in the temperature, the diode current exponentially decreases and vice versa. However, there is one more term mentioned in this equation, which is the saturation current\[({{I}_{0}})\], the variation for which is much greater than the exponential term.
ZENER DIODE
Zener Diode is a special purpose silicon PN junction diode which differs from other diodes in the sense that it operates in the reverse biased mode.
Zener diode is also known as a voltage regulator or voltage reference or breakdown diode. The Fig. shows the symbol for a zener diode:
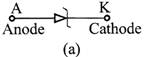Fig.: Symbol of Zener Diode
The breakdown voltage of a Zener diode is carefully controlled by maintaining the doping level during manufacturing. So, if the doping level is high, then depletion layer is thin and breakdown occurs at a low reverse voltage. When reverse voltage is increased, a critical voltage called breakdown voltage is reached at which reverse current will sharply increase.
Zener more...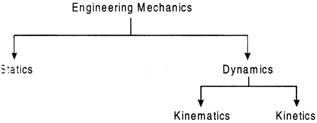 
Statics deals with forces in terms of their distribution and effect on a body at absolute or relative rest. Dynamics deals with the study of bodies in motion. Dynamics is further divided into kinematics and kinetics. Kinematics is concerned with the bodies in motion without taking into account the forces which are responsible for the motion. kinematics deals with the bodies in motion and its causes.
Force System: A force system may be coplanar/non-coplanar. in a coplanar force system, all the forces act in the same plane. In a non-coplanar force system, all the forces act in different planar.
Classification of force system: (For coplanar forces)
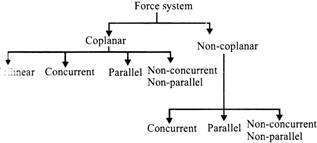(Complete classification of force system)
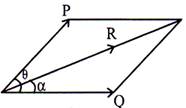Let \[\theta \]=Angle between the two forces 'P' and 'Q'
\[\alpha \]= Angle between resultant 'R' and one of the force
('Q' in this case)
= direction of the resultant then,
Then,
Resultant' \['R'=\sqrt{{{P}^{2}}+{{Q}^{2}}+2PQ\cos \theta }\]
Angle made by resultant \['R'=\left( \frac{P\sin \theta }{Q+P\cos \theta } \right)\]
or,
\[\tan \,\,\alpha =\left( \frac{P\sin \theta }{Q+P\cos \theta } \right)\Rightarrow \alpha ={{\tan }^{-1}}\left( \frac{P\sin \theta }{Q+P\cos \theta } \right)\]Land's theorem:
According to Lam is theorem, if three forces are acting at a point and the forces are in equilibrium, then the each of the three forces is directly proportional to the sine of the angle between the other two forces.
Let, P, Q, R = Three forces in equilibrium
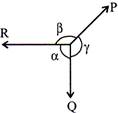\[\alpha \],\[\beta \], \[\gamma \]= Angles included between three forces P, Q and R then,
\[\frac{P}{\sin \alpha }=\frac{Q}{\sin more... 
TYPES OF THERMODYNAMIC SYSTEMS:
There are three types of thermodynamic systems:
(a) Closed system:
A thermodynamic system in which mass is not transferred across system boundary but energy may be transferred in and out of the system, is known as closed system. Mass in the piston - cylinder arrangement is the example of a more... 
Fig: Possibility of manufacturing in number of routes.
Broad classification of Engineering Manufacturing
Processes:
It is extremely difficult to tell the exact number of various manufacturing processes existing and are being practiced presently because a spectacularly large number of processes have been developed till now and the number is still increasing exponentially with the growing demands and rapid progress in science and technology. However, all such manufacturing processes can be broadly classified in four major groups as follows:
(a) Shaping or forming Manufacturing a solid product of definite size and shape from a given material taken in three possible states: in solid more... 
Functioning of a Computer
Computer Performs four basic functions -which are as follows
Components of Computer
A computer consists of following main components
