question_answer 6)

Consider the following figure of line \[\overset{\leftrightarrow }{\mathop{MN.}}\,\]Say whether following statements are true or false in context of the given figure. (a) Q, M, O, N, P are points on the line \[\overset{\leftrightarrow }{\mathop{MN.}}\,\] (b) M, O, N are points on a line segment \[\overline{MN}.\] (c) M and N are end points of line segment \[\overline{MN}.\] (d) O and N are end points of line segment \[\overline{OP}.\] (e) M is one of the end points of line segment\[\overline{QO}.\] (f) M is point on ray \[\overline{OP}.\] (g) Ray \[\overset{\to }{\mathop{OP}}\,\] is different from ray \[\overset{\to }{\mathop{QP}}\,.\] (h) Ray \[\overset{\to }{\mathop{OP}}\,\]is same as ray\[\overset{\to }{\mathop{OM}}\,.\] (i) Ray\[\overset{\to }{\mathop{OM}}\,\]is not opposite to ray \[\overset{\to }{\mathop{OP}}\,.\] (j) O is not an initial point of\[\overset{\to }{\mathop{OP}}\,.\] (k) N is the initial point of \[\overset{\to }{\mathop{NP}}\,\] and \[\overset{\to }{\mathop{NM}}\,.\]

Answer:

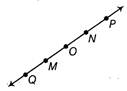
(a) True, because points M, O and N lie on the line \[\overset{\leftrightarrow }{\mathop{MN}}\,\]and points Q and Plie on the extended portion of \[\overset{\leftrightarrow }{\mathop{MN}}\,\] on both sides. (b) True, because points M, O, N lie on the line segment \[\overline{MN}.\] (c) True, because M to N is the shortest route of line segment \[\overline{MN}.\] (d) False, because it is clear from figure that point N is between O and P. (e) False, because it is clear from figure that point M is between Q and O. (f) False, because M is outside from ray \[\overset{\to }{\mathop{OP}}\,.\] (g) True, because all the rays have their own existence. (h) False, because rays \[\overset{\to }{\mathop{OP}}\,\] and \[\overset{\to }{\mathop{OM}}\,\] are in opposite directions. (i) True, because it is clear from figure that rays \[\overset{\to }{\mathop{OM}}\,\] and \[\overset{\to }{\mathop{OP}}\,\] are opposite. (j) False, because it is clear from figure that point O is the initial point of \[\overset{\leftrightarrow }{\mathop{OP}}\,.\] (k) True, because it is clear from figure that line segment \[\overline{NP}\] and \[\overline{NM}\]start from point N.