10th Class Mathematics Circles Circle

Circle

Circle

1. Secant: A line which intersects a circle in two distinct points.

2. Tangent: A line intersecting a circle only in one point is called a tangent to the circle at that point.

3. The tangent to a circle is perpendicular to the radius through the point of contract.

4. The point at which the tangent meets the circle is called the point of contact.

5. Length of Tangent: The length of the segment of the tangent from the given point P on the tangent to the point of         contact with the circle is called the length of the tangent from the point P to the circle.

6. The lengths of the two tangents from an external point to a circle are equal.

7. Number of tangents to a circle:

1. A circle is inscribed in a \[\Delta \,\mathbf{ABC}\] having sides 8 cm, 10 cm and 12 cm, as shown in the adjoining figure. Find the length of CF.

(a) 7 cm                        (b) 3 cm

            (c) 5 cm                         (d) 2 cm

            (e) None of these

Ans.     (b)

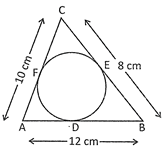
            Explanation: We know that the lengths of tangents to a circle from an external point are equal.

Let \[AD\text{ }=\text{ }AF\text{ }=\text{ }x\text{ }cm,\text{ }BD\text{ }=\text{ }BE\text{ }=\text{ }y\text{ }cm\text{ }and\text{ }CE\text{ }=\text{ }CF\text{ }=\text{ }z\text{ }cm\]

Now,     \[AB\text{ }=\text{ }12\,cm\] \[\Rightarrow \] \[AD\text{ }+\text{ }BD\text{ }=\text{ }12\text{ }cm\]  \[\Rightarrow \] \[x\text{ }+\text{ }y\text{ }=\text{ }12\text{ }cm\]              ..... (i)

\[BC\text{ }=\text{ }8\text{ }cm\]  \[\Rightarrow \] \[BE\text{ }+\text{ }CE\text{ }=\text{ }8\text{ }cm\]   \[\Rightarrow \] \[y\text{ }+\text{ }z\text{ }=\text{ }8\text{ }cm\]              .... (ii)

and       \[AC\text{ }=\text{ }10\text{ }cm\]\[\Rightarrow \] \[AF\text{ }+\text{ }CF\text{ }=\text{ }10\text{ }cm\]  \[\Rightarrow \] \[x\text{ }+\text{ }z\text{ }=\text{ }10\text{ }cm\]              .... (iii)

            Adding (i), (ii) and (iii) we get:

\[2\left( x\text{ }+\text{ }y\text{ }+\text{ }z \right)=30\] \[\Rightarrow \] \[x\text{ }+\text{ }y\text{ }+\text{ }z\text{ }=\text{ }15\]            ...(iv)

            From (i) and (iv) we get: \[z\text{ }=\text{ }3\text{ }cm\].

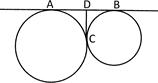
2.         In the following figure, AB and CD are two common tangents to the two touching circles. If DC = 4 cm then find the length of AB.
       

(a) 2 cm                        (b) 8 cm

            (c) 10 cm                       (d) 12 cm

            (e) None of these

Ans.     (b)

Explanation: We know that the lengths of two tangents drawn to a circle from a point outside the circle are equal.

            So, \[DA\text{ }=\text{ }DC\text{ }and\text{ }DB\text{ }=\text{ }DC\]

\[\therefore \]      \[AB\text{ }=\text{ }DA\text{ }+\text{ }DB\text{ }=\text{ }2DC\text{ }=\text{ }8\text{ }cm\]

3. If four sides of a quadrilateral ABCD are tangential to a circle, then

            (a) \[AB\text{ }+\text{ }CD\text{ }=\text{ }BC\text{ }+\text{ }AD\]        

(b) \[AC\text{ }+\text{ }AD\text{ }=\text{ }BD\text{ }+\text{ }CD\]

            (c) \[AB\text{ }+\text{ }CD\text{ }=\text{ }AC\text{ }+\text{ }BC\]        

(d) \[AC\text{ }+\text{ }AD\text{ }=\text{ }BC\text{ }+\text{ }DB\]

            (e) None of these

Ans.     (a)

            Explanation: We know that the tangents to a circle from a point outside it are equal.

So, \[AP\text{ }=\text{ }AS,\text{ }BP\text{ }=\text{ }BQ,\text{ }CQ\text{ }=\text{ }CR\] and \[DR\text{ }=\text{ }DS\]

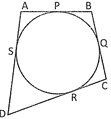
\[\therefore \]             \[AP\text{ }+\text{ }BP\text{ }+\text{ }CR\text{ }+\text{ }DR\text{ }=\text{ }AS\text{ }+\text{ }BQ\text{ }+\text{ }CQ\text{ }+\text{ }DS\]

\[\Rightarrow \]   \[\left( AP\text{ }+\text{ }BP \right)\text{ }+\text{ }\left( CR\text{ }+\text{ }DR \right)\text{ }=\text{ }\left( AS\text{ }+\text{ }DS \right)\text{ }+\text{ }\left( BQ\text{ }+\text{ }CQ \right)\]

                \[\Rightarrow \] \[AB\text{ }+\text{ }CD\text{ }=\text{ }AD\text{ }+\text{ }BC\]

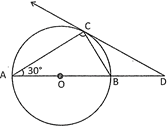
4.         AB is a diameter and AC is a chord of the circle given below. If \[\angle \,\mathbf{BAC}\text{ }=\text{ }\mathbf{30}{}^\circ \]and the tangent at C intersects AB produced in D, then,

(a) \[BC\text{ }<\text{ }BD\]                 

(b) \[BC\text{ }>\text{ }BD\]

            (c) \[BC\text{ }=\text{ }BD\]                 

(d) None of these

            (e) None of these

Ans.     (c)

            Explanation: According to the figure \[\angle \,ACB\text{ }=\text{ }90{}^\circ \]

\[\therefore \] \[\angle \,ABC=60{}^\circ \text{ }[\angle \,ABC=180{}^\circ -(Because\,\,\angle \,180{}^\circ \text{ }-\text{ }(\angle \,BAC\text{ }+\angle \,ACB)=180{}^\circ -\left( 30{}^\circ \text{ }+\text{ }90{}^\circ  \right)\text{ }=\text{ }60{}^\circ ]\]

            And so,        \[\angle \,CBD\text{ }=\text{ }120{}^\circ \]

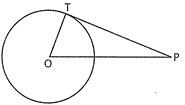
Also,     \[\angle \,BCD\text{ }=\angle \,BAC\text{ }=\text{ }30{}^\circ \] (angles in alternate segments)

\[\angle \,BDC\text{ }=\text{ }180{}^\circ \text{ }-\left( 30{}^\circ \text{ }+\text{ }120{}^\circ  \right)\text{ }=\text{ }30{}^\circ \]

            Thus,    \[\angle \,BCD\text{ }=\angle \,BDC.\text{ }\,So,\text{ }BC\text{ }=\text{ }BD.\]

5. ACB is a tangent to a circle at C. CD and CE are chords such that \[\angle \,\mathbf{ACE}\text{ }>\angle \,\mathbf{ACD}.\text{ }\mathbf{If}\,\,\angle \,\mathbf{ACD}\text{ }=\]

            \[\angle \,\mathbf{BCE}\text{ }=\text{ }\mathbf{50}{}^\circ \] then:

            (a) ED is not parallel to AB                     

            (b) \[CD\text{ }=\text{ }CE\]

            (c) ED passes through the centre of the circle

            (d) None of these

Ans.     (b)

            Explanation: In the following figure Join ED. Then we get,

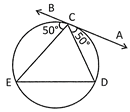
\[\angle \,DEC\text{ }=\angle \,ACD\text{ }=\text{ }50{}^\circ \] (angles in alternate segments)

And \[\angle \,EDC\text{ }=\angle \,BCE\text{ }=\text{ }50{}^\circ \] (angles in alternate segments)

            \[\angle \,DEC\text{ }=\angle \,EDC.\]

            So,       \[CD\text{ }=\text{ }CE\]