10th Class Mathematics Related to Competitive Exam Geometry

Geometry

In this chapter we will discuss about the similarity of triangles and properties of circles. Two figures having the same shape and not necessarily the same size are called the similar figures. Two polygons of the same number of sides are similar if their corresponding angles are equal and their corresponding sides are in the same ratio. Circle is defined as the locus of a point which is at a constant distance from a fixed point. The fixed point is called the canter of the circle and the fixed distance is called the radius of the circle.

Similar Triangles

Two triangles are similar, if their corresponding angles are equal and their corresponding sides are in the same ratio. The ratio of any two corresponding sides in two equiangular triangles is always the same.

Basic Proportionality Theorem

It states that if a line is drawn parallel to one side of a triangle to intersect the other two sides in the distinct points, the other two sides are divided in the same ratio. Conversely, if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side of the triangle.

Area of Similar Triangles

It states that the ratio of area of two similar triangles is equal to the square of the ratio of their corresponding sides.

Tangent to a Circle

A tangent to a circle is a line which intersects the circle at exactly one point. The point where the tangent intersects the circle is known as the point of contact.

Properties of tangent to a circle

Following are some properties of tangent to a circle:

•          A tangent to a circle is perpendicular to the radius through the point of contact.
•          A line drawn through the end-point of a radius and perpendicular to it is a tangent to the circle.
•         The lengths of the two tangents drawn from an external point to a circle are equal.
•          If two tangents are drawn to a circle from an external point, they subtend equal angles at the centre.
•          If two tangents are drawn to a circle from an external point, then they are equally inclined to the segment, joining the centre to that point.

From the above points we conclude that in the following figure;

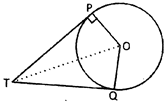
\[\angle \]OPT = \[\angle \]OQT = \[90{}^\circ \], \[\angle \]POT = \[\angle \]QOT

\[\angle \]QTO = \[\angle \]OTP and PT = QT.

Example:

Two tangents PT and QT are drawn to a circle with centre 0 from an external point as shown in the following figure, then:

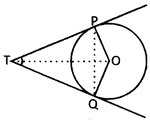
(a) \[\angle \]QTP = \[\angle \]QPO                                                (b) \[\angle \]QTP = 2\[\angle \]QPO

(c) \[\angle \]QTP = 3\[\angle \]QPO                                             (d) \[\angle \]QTP =\[90{}^\circ \]

(e) None of these

Ans.     (b)

Explanation: In the given figure, we have

TP = TQ [tangents drawn from an external point are equal in length]

\[\Rightarrow \]\[\angle \]TPQ = \[\angle \]TQP

In \[\Delta \]TPQ, we have \[\angle \]TPQ + \[\angle \]TQP + \[\angle \]PTQ =\[180{}^\circ \]

\[\Rightarrow 2\,\angle TPQ=180{}^\circ -\angle PTQ\]

\[\Rightarrow \,\angle TPQ=90{}^\circ -\angle PTQ\]                                                                                         .......... (i)

Also, \[\angle OPT=90{}^\circ \Rightarrow \angle OPQ=90{}^\circ -\angle TPQ\]                           .......... (ii)

From (i) and (ii), we get  \[\frac{1}{2}\angle \,PTQ=\angle OPQ\Rightarrow \angle PTQ=2\,\angle OPQ\]