10th Class Mathematics Introduction to Trigonometry

Introduction to Trigonometry

• Trigonometry: The branch of mathematics that deals with the study of relationships between the sides and angles of a triangle is called trigonometry.

• The word 'trigonometry' is derived from the greek words 'tri' meaning three, 'gon' meaning sides and 'metron' meaning measure.

• Trigonometric ratios: In right AABC, AB is the hypotenuse, AB is the side opposite to \[\angle C(=\theta )\], and BC is the side adjacent to 6.

The trigonometric ratios for angle \[\theta \]:                     
                    

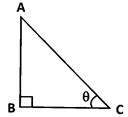
(a) \[\sin \theta =\frac{side\,opposite\,to\,\theta }{Hypotenuse}=\frac{AB}{AC}\]

(b) \[\cos \theta =\frac{side\,adjacent\,to\,\theta }{Hypotenuse}=\frac{BC}{AC}\]

(c) \[\tan \theta =\frac{side\,opposite\,to\,\theta }{side\,adjacent\,to\,\theta }=\frac{AB}{BC}\]

(d) \[\cos ec\theta =\frac{Hypotenuse}{side\,opposite\,to\,\theta }=\frac{AC}{AB}\]

(e) \[sec\theta =\frac{Hypotenuse}{side\,adjacent\,to\,\theta }=\frac{AC}{BC}\]

(f) \[\cot \theta =\frac{side\,adjacent\,to\,\theta }{side\,opposite\,to\,\theta }=\frac{BC}{AB}\]  

• Full names of the trigonometric ratios: sin = sine; cos = cosine; tan = tangent; cosec = cosecant; sec = secant; cot = cotangent

Note: (a) \[\sin \theta \] is a single symbol. It does not mean the product of sine and\[\theta \].

(b) In short, t-ratios is used for trigonometric ratios.

(c) Trigonometric ratios are real numbers.

• Reciprocal relations: The reciprocal relations for the trigonometric ratios are
  (a) \[\frac{1}{\sin \theta }=\cos ec\theta \] (b) \[\frac{1}{\cos \theta }=sec\theta \]

(c) \[\frac{1}{\tan \theta }=\cot \theta \]

• Quotient relations:

(a) \[\tan \theta =\frac{\sin \theta }{\cos \theta }\]        (b) \[\cot \theta =\frac{\cos \theta }{\sin \theta }\]

• Values of trigonometric ratios: The values of trigonometric ratios remain the same for the same angle of different right triangles.

Note: A trigonometric ratio depends on the magnitude of the angle and not on its size.

• Trigonometric ratios of complementary angles:

If\[\theta \] is acute, then

(a) \[\sin ({{90}^{o}}-\theta )=\cos \theta \] 

(b) \[\cos ({{90}^{o}}-\theta )=\sin \theta \]    

(c) \[\tan ({{90}^{o}}-\theta )=\cot \theta \]

(d) \[\cot ({{90}^{o}}-\theta )=\tan \theta \]

(e) \[\sec ({{90}^{o}}-\theta )=\cos ec\theta \]

(f) \[co\sec ({{90}^{o}}-\theta )=sec\theta \]

• Trigonometric identities: An equation involving trigonometric ratios of angle\[\theta \]is said to be an identity if it is satisfied for all values of\[\theta \].

(a) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]

(b) \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]

(c) \[co{{\sec }^{2}}\theta -{{\cot }^{2}}\theta =1\]

• Some equations derived from trigonometric identities:

(a) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]

\[\Rightarrow \] \[{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \]

\[\Rightarrow \] \[\sin \theta =\sqrt{1-{{\cos }^{2}}\theta }\]

Similarly,

\[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]

\[\Rightarrow \] \[\cos \theta =\sqrt{1-{{\sin }^{2}}\theta }\]

(b) \[{{\sec }^{2}}q-{{\tan }^{2}}\theta =1\]

\[\Rightarrow \] \[{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta \]

\[\Rightarrow \] \[\sec \theta =\sqrt{1+{{\tan }^{2}}\theta }\]

Similarly,

\[{{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1\]

\[\Rightarrow \] \[\tan \theta =\sqrt{{{\sec }^{2}}\theta -1}\]

• Some more trigonometric identities:

(a) \[\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta \]

(b) \[\sin 2\theta =2\sin \theta \cos \theta \]

(c) \[\cos 2\theta ={{\cos }^{2}}\theta -{{\sin }^{2}}\theta \]

(d) \[\frac{{{\tan }^{2}}\theta }{1+{{\tan }^{2}}\theta }=si{{n}^{2}}\theta \]

(e) \[2{{\cos }^{2}}\theta -1=\frac{-1{{\tan }^{2}}\theta }{1+{{\tan }^{2}}\theta }\]

(f) \[\tan 2\theta =\frac{2\tan \theta }{1-{{\tan }^{2}}\theta }\]

• Relations expressing one trigonometric ratios in terms of the other