10th Class Mathematics Introduction to Trigonometry Trigonometrical Identities

       Trigonometrical Identities

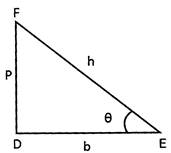
In the adjoining figure triangle DEF is a right angled triangle right angle at D. Then the trigonometrical identities are

1. \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]

2. \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]

3. \[co{{\sec }^{2}}\theta -{{\cot }^{2}}\theta =1\]  

We can also derive different relations between identities in different form

(a) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]             

or \[{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \]

or \[\sin \theta =\pm \sqrt{1-{{\cos }^{2}}\theta }\]

Similarly                

\[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]

or \[\cos \theta =\pm \sqrt{1-{{\sin }^{2}}\theta }\]

(b) \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]

or \[{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta \]

or \[{{\sec }^{2}}\theta =\sqrt{1+{{\tan }^{2}}\theta }\]

Similarly                

\[{{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1\]

or           \[\tan \theta =\pm \sqrt{{{\sec }^{2}}\theta -1}\]

(c) \[\cos e{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\]

or            \[\cos e{{c}^{2}}\theta =1+{{\cot }^{2}}\theta \]

or            \[\cos e{{c}^{2}}\theta =\pm \sqrt{1+{{\cot }^{2}}\theta }\]

Similarly

\[{{\cot }^{2}}\theta =\cos e{{c}^{2}}\theta -1\]

or \[\cot \theta =\pm \sqrt{\cos e{{c}^{2}}\theta -1}\]  

Verification of \[\mathbf{si}{{\mathbf{n}}^{\mathbf{2}}}\mathbf{\theta +co}{{\mathbf{s}}^{\mathbf{2}}}\mathbf{\theta =1}\]

Suppose \[\Delta \text{RST}\] is a right angled triangle in which right angle at R and angle S in formed at\[\theta \].

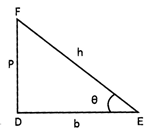
Here, perpendicular RT represented by "p", base RS represented by "b" and hypotenuse "ST" represented by h.

Then by Pythagoras theorem,

\[{{p}^{2}}+{{b}^{2}}={{h}^{2}}\]

As we know

\[\sin \theta =\frac{p}{h},\] \[\cos \theta =\frac{b}{h}\]

Therefore,

\[{{\sin }^{2}}\theta =\frac{{{p}^{2}}}{{{h}^{2}}}\,\,\text{and}\,\,{{\cos }^{2}}\theta =\frac{{{b}^{2}}}{{{h}^{2}}}\]

\[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =\frac{{{p}^{2}}}{{{h}^{2}}}+\frac{{{b}^{2}}}{{{h}^{2}}}=\frac{{{p}^{2}}+{{b}^{2}}}{{{h}^{2}}}=\frac{{{h}^{2}}}{{{h}^{2}}}=1\]

Therefore, \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]

Similarly we can verify other results.  

            Values of Different Trigonometrical Ratios in Different Quadrants

Above shows the different quadrants. The following are about the T- Ratios when angles lies in different quadrants

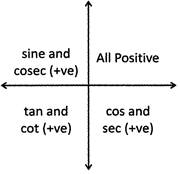
1.    When the angle lies in the I quadrant all trigonometrical ratios are positive i.e. The value of \[\text{sin}\theta ,\text{ cos}\theta ,\text{ tan}\theta ,\text{ cot}\theta ,\text{ sec}\theta \]and \[\text{cosec}\theta \] are positive.

2.    When the angle\[''\theta ''\] lies in the second quadrant, the value of sine and cosec are positive and other ratios like \[\text{cos}\theta ,\text{ tan}\theta ,\text{ cot}\theta \] and \[\text{sec}\theta \] are negative.

3.    When an angle \[''\theta ''\] lies in third quadrant, the value of tan e and cote are positive and other ratios like \[\text{sin}\theta \text{,}\,\text{cos}\theta ,\text{ cosec}\theta \]and \[\sec \theta \] are negative.

4.    When an angle \[''\theta ''\] lies in fourth quadrant, the value of \[\text{cos}\theta \text{ sec}\theta \] are positive and other ratios like \[\text{sin}\theta ,\text{ tan}\theta ,\text{ cosec}\theta \] and cote are negative.

From the figure given below you can remember it easily