Polynomials
Category : 10th Class
Polynomials
Polynomials are algebraic expressions having finite terms. The expression \[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+{{a}_{n-2}}{{x}^{n-2}}+---+{{a}_{1}}x+{{a}_{0}}\] is called the polynomial of degree n, where \[{{a}_{n}}\ne 0.\] The highest power of the variable in a polynomial is called degree of the polynomial. The polynomials of degree one are called linear polynomial. The polynomials of degree two are called quadratic polynomials. The polynomials of degree three are called cubic polynomials and the polynomials of degree four are called biquadratic polynomials. A real number which satisfies the given polynomial is called zero of the polynomial.
Zeroes of a Polynomial
If \[a{{x}^{2}}+\text{ }bx\text{ }+\text{ }c\text{ }=\text{ }0,\text{ }(a\ne o),\]is a quadratic equation whose roots are \[\alpha \] and \[\beta \], then the relation between the roots of the equation and its coefficients is given by:
Sum of the roots =\[\alpha +\beta =-\frac{b}{a},\]
Product of the roots = \[\alpha \beta =\frac{c}{a}.\]
For a cubic equation \[a{{x}^{3}}+\text{ }b{{x}^{2}}+\text{ }ex\text{ }+\text{ }d\]= 0 (a = 0) roots are a, P and y, the relation between the roots of the equation and its coefficients is given by
Sum of roots =\[\alpha +\beta +\gamma =-\frac{b}{a},\]
Sum of the product of roots =\[\alpha \beta +\beta \gamma +\gamma \alpha =\frac{c}{a},\]
Product of the roots =\[\alpha \beta \gamma =-\frac{d}{a},\]
The zeroes of the polynomials \[\mathbf{6}{{\mathbf{x}}^{\mathbf{2}}}-\text{ }\mathbf{x}\text{ }-\text{ }\mathbf{2}\] are:
(a) \[\frac{1}{3}and\frac{2}{3}\] (b) \[\frac{-1}{3}and\frac{1}{2}\]
(c) \[\frac{2}{3}and\frac{-1}{2}\] (d) \[\frac{-2}{3}and\frac{1}{2}\]
(e) None of these
Ans. (c)
Explanation: Let f(x) = \[6{{x}^{2}}-\text{ }x\text{ }-\text{ }2.\]
By the method of splitting the middle term, we have
\[f\,(x)=\text{ }6{{x}^{2}}-x-2=6{{x}^{2}}-4x+3x-2\]
\[=2x\left( 3x-2 \right)+1\left( 3x-2 \right)=\left( 2x+1 \right)\left( 3x-2 \right)\]
Zeroes of (x) will be obtained by putting
\[2x+\text{ }1=0\]and \[3x-2=0\] \[\Rightarrow x=\frac{-1}{2}\,\,and\,\,x=\frac{2}{3}\]
Division of Polynomials
Previously we have studied about the division of the real numbers, in which we obtained quotient and remainder which satisfy the relation:
Dividend = Quotient \[\times \] Divisor + Remainder
This is also known as Euclid's division lemma. In this section we will discuss about the division of the polynomials which is known as the division algorithm for polynomials. The concept of division of the polynomials can be used for finding the zeroes of the cubic or biquadratic polynomials.
For example, when we divide g(x) \[=\text{ }{{x}^{3}}-\text{ }3{{x}^{2}}+\text{ }3x\text{ }-\text{ }5\text{ }by\text{ }h\left( x \right)\text{ }=\text{ }{{x}^{2}}+\text{ }x\text{ }+\text{ }1\]we have,
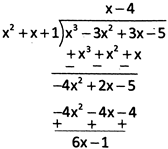
Here we have quotient \[q\left( x \right)=x-4,\] and remainder \[r\left( x \right)=6x-1\].
Graph of Polynomials
In this section we will learn about the construction of linear, quadratic and cubic polynomial graphs. In order to draw a graph of the polynomial f(x), we first find some values of x which satisfy the equation of f(x) and plot these points on a rectangular co-ordinate system and then join these points with free hand curve.
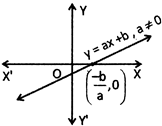
Graph of a Linear Polynomial
We know that ax + b is a linear polynomial. So the graph of y = ax + b is as follows:
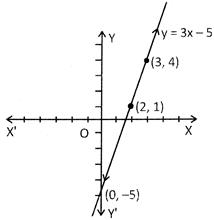
Draw the graph of the polynomial given by\[\mathbf{f}\left( \mathbf{x} \right)=\mathbf{3x}-\mathbf{5}\].
Solution: Let \[y=3x-5,\] then the following table will represent the values of x and y which satisfy the given equation.
|
x |
2 |
3 |
0 |
|
f(x) = y |
1 |
4 |
\[-\]5 |
Graph of a Quadratic Polynomial
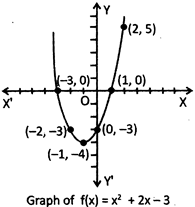
We know that \[y=a{{x}^{2}}+bx+c,a\ne o\]is a quadratic polynomial. In general the graph of a quadratic polynomial is a parabola with the horns pointing upwards if a > 0 or downwards if a < 0.
Draw the graph of the polynomial given by \[\mathbf{f}\left( \mathbf{x} \right)\text{ }=\text{ }{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{2x}\text{ }-\text{ }\mathbf{3}\]
Solution: To draw the graph of the given polynomial, first make the following table:
|
X |
0 |
1 |
\[-\]1 |
2 |
\[-\]2 |
\[-\]3 |
|
f(x) = y |
\[-\]3 |
0 |
\[-\]4 |
5 |
\[-\]3 |
0 |
Now plot these points on a graph paper and join these points with smooth hand curve to get the graph which is shown below.
Graph of a Cubic Polynomial
We know that graph of a quadratic polynomial is a parabola either opening upwards or downwards but graph of a cubic polynomial does not have a fixed shape. The graph of a cubic polynomial can be made by joining the ordered pair of the given equation. The graph of a cubic polynomial always cuts x-axis atleast once and atmost thrice.
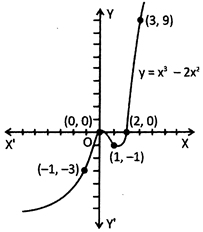
Draw the graph of the polynomial \[\mathbf{f}\left( \mathbf{x} \right)=\text{ }{{\mathbf{x}}^{\mathbf{3}}}-\text{ }\mathbf{2}{{\mathbf{x}}^{\mathbf{2}}}.\]
Solution: Let us make a table of \[y\text{ }=\text{ }{{x}^{3}}-\text{ }2{{x}^{2}}\]for different values of x.
|
x |
0 |
1 |
2 |
\[-\]1 |
3 |
|
f(x) = y |
0 |
\[-\]1 |
0 |
\[-\]3 |
9 |
Now plot these point on the graph to obtain the following graph:
You need to login to perform this action.
You will be redirected in
3 sec
