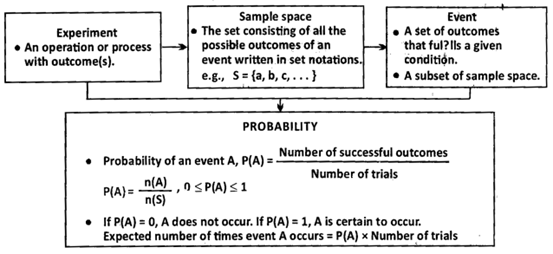
10th Class Mathematics Probability

 Probability

• Random experiment: An experiment in which all possible outcomes are known and the exact outcome cannot be predicted in advance is called a random experiment.

e.g., (1) Tossing a coin.

(2) Rolling an unbiased die.

• Sample space:

The set S of all possible outcomes of a random experiment is called the sample space.

e.g., (1) In tossing a coin, sample space (S) = {H,T}.

• (2) In rolling a die, sample space (S) = {1, 2, 3, 4, 5, 6}.

• Probability: Probability is a concept which numerically measures the degree of certainty of the occurrence of events.

• Definition of probability: in a random experiment, let S be the sample space arid let E be an event. Then probability of occurrence of \[E=P(E)=\frac{n(E)}{n(S)}\],where  

n(E) is the number of elements favorable in E and

n(S) is the number of distinct elements in S.

Note :  1. \[0\le P(E)\le 1\]

2. If \[P(E)=1\], The event E is called a certain event and if \[P(E)=0\], the event E is called an impossible event.

• Types of events:

• (i) Simple event or elementary event: An event is called a 'simple event; if it is a single- ton subset of the sample space's'.

e.g.. When a coin is tossed, sample space S = {H,T}

Let A = {H} = The event of occurrence of head and

B = {T}= The event of occurrence of tail.

Then 'A' and 'B' are simple events.

(ii) Mixed event or compound event: A subset of the sample space 'S' which contains more than one element is called a compound event.

e.g.. When a die is thrown, sample space S = {1, 2, 3, 4, 5, 6}.

Let A = {1,3,5} = The event of occurrence of odd number and

B = {5,6} = The event of occurrence of a number greater than 4.

Then, A' and 'B' are compound events.

(iii) Sure event: If a random experiment 'E' has a discrete sample space 'S’; then 'S' itself is an event (E = S) called the sure or certain event of 'E'.

e.g.. Getting a head or a tail in a single toss of a coin is a sure event.

The probability of a sure event (or certain event) is 1.

(iv) Impossible event: The empty subset \['\phi '\]of 'S' \[(E=\{\})\]is called the impossible event or null event of 'E'.

e.g.. Getting a head and a tail. both in a single toss of a coin is an impossible event.

The probability of an impossible event is 0.

(v) Complementary event: For a random event 'A' of a random experiment 'E; the event complementary to 'A' is the event that "A does not occur" It is denoted by A' or A'= or A.

(vi) Equally likely events: Events are said to be equally likely when there is no reason to expect any one of them rather than any one of the others.

e.g.. When an unbiased die is thrown, all the six faces 1, 2, 3, 4, 5 and 6 are-equally likely to come up.

• Results based on the definition of probability: The following results are direct consequences of the definition of probability.

(i) If 'E' is an event of sample space's', then\[0\le P(E)\le 1\].

P(E) = 0 if and only if 'E' is an impossible event and

P(E) = 1 if and only if 'E' is a certain event. (ii) If 'E' is an event of sample space 'S' and 'E' (or I) is the event that E does not happen, then \[P(E')=1-P(E)\].

• Odds in favour and odds against: Let 'A' be an event of an experiment 'E'. Then, the ratio P(a) :P(A') is called the odds in favour of A and the ratio P(A'): P(a) is called the ‘odds against' A.

• Combination of two events:

(i) Union of events:

If A and Bare two events of the sample space S, then \[A\cup B(orA+B)\]is the event that either A or B (or both) take place.

• (ii) Intersection of events:

If A and B are two events of the sample space 'S’; then \[A\cap B\] (or AB) is the event that both A and B take place.

• (iii) Mutually exclusive events:

Two events A and B of the sample space S are said to be mutually exclusive if they cannot occur simultaneously. In such a case \[A\cap B\]is a null set.

e.g.. When two coins are tossed the number of elementary events is 4 and they are (H, H), (H, T), (T, H), (T, T).These are mutually exclusive.

• (iv) Exhaustive event:

Two events A and B of the smaple space S are said to be exhaustive if \[A\cup B=S\], i.e., \[A\cup B\]contains all sample points.

e.g.. In tossing a coin, there are two exhaustive elementary events.

They are head and tail.

Note:

(a)A and A' are mutually exclusive as well as exhaustive events, as \[A\cap A'=\{\,\,\,\}\]and \[A\cup A'=S\]

(b) A - B denotes the occurrence of event A but not B. Thus, A - B occurs \[\Leftrightarrow A\]occurs and B does not occur.

Clearly, \[A-B=A\cap B',B-A=B\cap A'\].

• Addition theorem of probability: If A and B are any two events in a sample space S, then the probability of occurrence of at least one of the events A and B is given by\[P(A\cup B)=P(A)+P(B)\].

• Note:

(i) If A and B are mutually exclusive events, then \[A\cap B=\phi \]and hence, \[P(A\cap B)=0\].

\[\therefore \] \[P(A\cup B)=P(A)+P(B)\]

(ii) Two events A and B are mutually exclusive if and only if \[P(A\cup B)=P(A)+P(B)\]