REAL NUMBER
FUNDAMENTALS
- Rational numbers: Numbers which can be written in the form of\[\frac{p}{q}(q\ne 0)\], where p and q are integers, are called rational numbers.
Note: Every terminating decimal and non-terminating repeating decimal can be expressed as a rational number,
- Irrational numbers: Numbers which cannot be written in the form of \[\frac{p}{q}\]where p and q are integers and q ^ 0 are called irrational, numbers. Numbers which are not rational are called irrational numbers.
- Real numbers: The rational numbers and the irrational numbers together are called real numbers. Both rational & irrational numbers real line on number line.
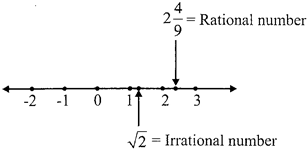
Note: Any number that can be represented on a number line is called a real number.
- Lemma: A proven statement which is used to prove another statement is called a lemma.
- Euclid’s division lemma: For any two positive integers ‘a’ and ‘b’, there exist whole numbers ‘q’ and ‘r’ such that \[a=bq+r,0\le r<b\]
This is an extension of the idea:
Dividend = Divisor x quotient + Remainder
(a) (b) (q) (r)
Remainder ‘r’ is always less than divisor (b) (This is basic principle of mathematics).
Note: Euclid’s division algorithm is stated only for positive integers, but can be extended/or all negative integers.
- Algorithm: An algorithm is a process of solving particular problems.
- Euclid’s division algorithm is used to find the Highest Common Factor (H.C.F.) of two numbers.
- Following is the procedure for finding H.C.F. using Euclid’s division algorithm: Suppose the two positive numbers are ‘a’ and ‘b’, such that a > b. Then the H.C.F. of ‘a’ and ‘b’ can be found by following the steps given.
(a) Apply the division lemma to find ‘q’ and ‘r’ where \[a=bq+r,0\le r<b\].
(b) If r = 0, then\[H.C.F.\,\,is\,\,b.\,\,If\,\,r\ne 0\], then apply Euclid's lemma to find ‘b’ and ‘r’.
- Continue steps (a) and (b) till r = 0. The divisor at this state will be H.C.F. (a, b). Also, H.C.F. (a, b) = H.C.F. (b, r).
- Fundamental theorem of Arithmetic: Every composite number can be expressed as a unique product of prime numbers. This is also called the prime factorization theorem.
Note: (i) The order in which the prime factors occur is immaterial.
In general, any composite number x, can be expressed as a product of prime numbers
Elementary Question: 1
Find HCF of 6 and 16.
Also verify that HCF of 18 and 48 is 3 times HCF of 6 and 16.
Sol.: 6 and 16: \[6=2\times 3\]
\[16=2\times 2\times 2\times 2\text{ }\therefore {{\left( HCF \right)}_{1}}=2\]
- and 48: \[18=2\times 3\times 3;\] \[48=2\times 2\times 2\times 2\times 3\]
\[\therefore {{(HCF)}_{2}}=2\times 3=6;\] \[\therefore {{\left( HCF \right)}_{2}}=\text{ }3\times {{\left( HCF \right)}_{1}}\]
Elementary Question: 2
Do the above problem by Euclid is division algorithm.
- C.M. of \[\frac{a}{b}\] and \[\frac{c}{d}=\frac{L.C.M.\,\,of\,\,a\,\,and\,\,c}{H.C.F.\,\,of\,\,b\,\,and\,\,d}=\frac{L.C.M.\,\,(a,c)}{H.C.F.\,\,(b,d)}.\]
- Some Important Result on Natural Numbers
- \[1+2+3+----------+n=\frac{n(n+1)}{2}\]
- \[{{1}^{2}}+{{2}^{2}}+{{3}^{2}}+----------+{{n}^{2}}=\frac{n(n+1)(2n+1)}{6}\]
- \[{{1}^{3}}+{{2}^{3}}+{{3}^{3}}+----------+{{n}^{3}}={{\left[ \frac{n(n+1)}{2} \right]}^{2}}\]
- \[{{x}^{n}}+{{y}^{n}}\] is divisible by \[\left( x\text{ }+y \right)\]if n is odd.
- \[{{x}^{n}}-{{y}^{n}}\]is divisible by \[\left( x\text{ }-\text{ }y \right)\] for all values of n.
- If a number is divisible by m and n, then it is always divisible by the LCM of m and n.
- \[{{x}^{n}}-{{y}^{n}}\]is divisible by \[\left( x\text{ }+y \right)\] if n is even.

