Trigonometry and Its Application
Category : 10th Class
Trigonometry and Its Application
The word trigonometry is a Greek word consists of two parts 'trigonon' and 'metron' which means measurements of the sides and angles of a triangle. This was basically developed to find the solutions of the problems related to the triangles in the geometry. Initially we use to measure angles in terms of degree, but now we will use another unit of measurement of angles called radians. The relation between the radian and degree measure is given by:
1 radians \[={{\left( \frac{180}{\pi } \right)}^{o}}\]and 1o=\[{{\left( \frac{\pi }{180} \right)}^{o}}\]radians or \[{{\pi }^{c}}\]=\[{{180}^{o}}\]
Trigonametric ratios of allied angles
Two angles are called allied angles when their sum or difference is either zero or a multiple of\[90{}^\circ \]. The angles\[-\,\theta ,\text{ }90{}^\circ \pm \text{ }\theta ,\]\[180{}^\circ +\text{ }\theta ,\] etc. are angles allied to the angles \[\theta \] where \[\theta \] is measured in degrees.
|
\[\theta \] |
\[\sin \theta \] |
\[\cos \theta \] |
\[\tan \theta \] |
\[\text{cosec}\,\theta \] |
\[\sec \theta \] |
\[\cot \theta \] |
|
\[-\,\theta \] |
\[-\,\sin \theta \] |
\[\cos \theta \] |
\[-\,\tan \theta \] |
\[-\,\text{cosec}\,\theta \] |
\[\sec \theta \] |
\[-\cot \theta \] |
|
\[90{}^\circ -\,\theta \] |
\[\cos \theta \] |
\[\sin \theta \] |
\[\cot \theta \] |
\[\sec \theta \] |
\[\text{cosec}\,\theta \] |
\[\tan \theta \] |
|
\[90{}^\circ +\theta \] |
\[\cos \theta \] |
\[-\,\sin \theta \] |
\[-\cot \theta \] |
\[\sec \theta \] |
\[-\,\text{cosec}\,\theta \] |
\[-\,\tan \theta \] |
|
\[180{}^\circ -\theta \] |
\[\sin \theta \] |
\[-\,\cos \theta \] |
\[-\,\tan \theta \] |
\[\text{cosec}\,\theta \] |
\[-\sec \theta \] |
\[-\cot \theta \] |
|
\[180{}^\circ +\theta \] |
\[-\,\sin \theta \] |
\[-\,\cos \theta \] |
\[\tan \theta \] |
\[-\,\text{cosec}\,\theta \] |
\[-\sec \theta \] |
\[\cot \theta \] |
Trigonometric Identities
An equation involving trigonometric ratios of an angle \[\theta \] is said to be a trigonometric identity, if it is satisfied by all the values of\[\theta \]. In this chapter we will deal only with the following identities.
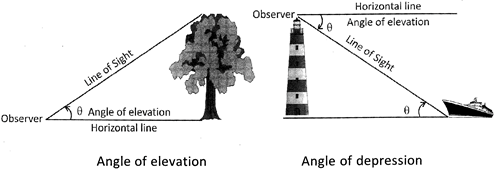
Angle of Elevation and Depression
The angle of elevation of an object as seen by an observer is the angle made between the horizontal and the line of sight. The angle made between the horizontal and the line of sight, if the object is placed below the observer's eye is called angle of depression.
A person standing on the top of a light house of height 200 m above sea level observes that the angle of depression of a ship sailing directly towards it changes from \[\mathbf{30}{}^\circ \] to\[\mathbf{45}{}^\circ \]. The distance travelled by the ship during this period is:
[Take \[\sqrt{\mathbf{3}}\]=1.73]
(a) 73 m (b) 128 m
(c) 146 m (d) 219 m
(e) None of these
Solution: Let the ship travelled a distance of x meters during the period of 200 observation, then in \[\Delta \]BCT, we have
\[\frac{200}{BC}=tan{{45}^{o}}\Rightarrow BC=200m\]
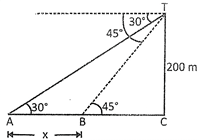
In \[\Delta \]ACT, we have \[\frac{200}{x+200}=tan{{30}^{o}}\Rightarrow x+200=200\sqrt{3}\]
\[\Rightarrow x=200(\sqrt{3}-1)m\] \[\Rightarrow x=200\times 0.73\Rightarrow x=146m\]
You need to login to perform this action.
You will be redirected in
3 sec
