10th Class Mathematics Triangles

 

Triangles

 

 

Triangles

 

1. Congruent Figures: Two figures which are alike in all respects i.e., which have the same shape and size are known as congruent figures.

 

2. Similar Figures: Two figures having the same shape but not necessarily the same size are known as similar figures.

 

3. All the congruent figures are similar but converse is not true.

 

4. Equiangular Triangles: Two triangles are said to be equiangular if their corresponding angles are equal.

 

5. Similar Triangles: Two triangles are said to be similar if their corresponding angles are equal and their             corresponding sides are proportional.

 

6. Two polygons of the same number of sides are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio.

 

7. If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangle are similar (AAA similarity).

 

8. If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are similar (AA similarity).

 

9. If in two triangles, corresponding sides are in the same ratio, then their corresponding angles are equal and hence the triangles are similar (SSS similarity).

 

10. If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportional), then the triangles are similar (SAS similarity).

 

11. The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

 

Snap Test

 

 

1. In the adjoining figure, if \[\mathbf{DE}\,~\parallel \mathbf{AB}\] and \[\mathbf{FE}~\,\,\parallel \,\,\mathbf{DB}\], then \[\mathbf{CF}.\mathbf{AC}\] =?

 

                      

           

          

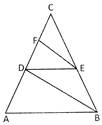
(a) \[F{{C}^{2}}\]          (b) \[F{{E}^{2}}\]       

            (c) \[D{{C}^{2}}\]        (d) \[D{{B}^{2}}\]

            (e) None of these

Ans.     (a)

            Explanation: In \[\Delta \,ABC\], it is given that \[DE\,\,~\parallel \,\,AB\].

 

            \[\therefore \,\,\,\,\,\frac{CD}{DA}=\frac{CE}{EB}\]                                 …….. (i)

 

            In \[\Delta \,CDB\], it is given that \[FE~\,\,\parallel \,\,DB\].

           

 

          

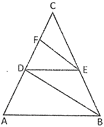
\[\therefore \,\,\,\,\,\frac{CF}{FD}=\frac{CE}{EB}\]                                  …….. (ii)

 

            From equations (i) and (ii), we get:

           

            \[\frac{CD}{DA}=\frac{CF}{FD}\]

 

\[\Rightarrow \,\,\,\,\frac{DA}{CD}=\frac{FD}{CF}\Rightarrow \,\,\,\,\frac{DA}{CD}+1\,\,\,=\,\frac{FD}{CF}+1\,\,\Rightarrow \,\,\,\frac{DA+CD}{CD}=\frac{FD+CF}{CF}\]

 

\[\Rightarrow \,\,\,\,\,\frac{AC}{CD}=\frac{DC}{CF}\,\,\,\,\,\,\,\,\Rightarrow \,\,D{{C}^{2}}=CF\times AC\]

 

2.         In the figure, AD is the bisector of \[\angle \,\mathbf{BAC}\]. If \[\mathbf{AB}\text{ }=\text{ }\mathbf{10}\text{ }\mathbf{cm}\], \[\mathbf{AC}\text{ }=\text{ }\mathbf{6}\text{ }\mathbf{cm}\text{ }\mathbf{and}\text{ }\mathbf{BC}\text{ }=\text{ }\mathbf{12}\text{ }\mathbf{cm}\], find BD and DC.

           

 

           

(a) 7.5 cm, 4.5 cm         (b) 6.5 cm, 4.5 cm

            (c) 7.5 cm, 2.5 cm          (d) 7.5 cm, 3.5 cm

            (e) None of these

Ans.     (a)

Explanation: Let \[BD\text{ }=\text{ }x\text{ }cm\]. Then \[DC\text{ }=\text{ }BC\text{ }-\text{ }BD\text{ }=\text{ }\left( 12\text{ }-\text{ }x \right)\text{ }cm\].

 

           

 

         

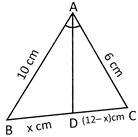
In \[\Delta \,ABC\], AD is the bisector of \[\angle \,BAC\].

 

            \[\therefore \,\,\,\,\,\frac{BD}{DC}\,\,=\,\,\frac{AB}{AC}\]

 

            \[\Rightarrow \,\,\,\,\frac{x}{12-x}=\frac{10}{6}\,\,\,\Rightarrow \,\,6x=120\,\,-\,\,10x\]

 

            \[\Rightarrow \,\,\,16x\,\,=\,\,120\,\,\,\Rightarrow \,\,\,x\,\,=\,\,7.5.\]

            Hence, \[BD\text{ }=\text{ }x\text{ }cm\text{ }=\text{ }7.5\text{ }cm\] and \[DC\text{ }=\text{ }\left( 12\text{ }-\text{ }x \right)\text{ }cm\text{ }=\text{ }\left( 12\text{ }-\text{ }7.5 \right)\text{ }cm\text{ }=\text{ }4.5\text{ }cm\].

 

3. The areas of two similar triangles ABC and DEF are \[\mathbf{64}\text{ }\mathbf{c}{{\mathbf{m}}^{\mathbf{2}}}\] and \[\mathbf{169}\text{ }\mathbf{c}{{\mathbf{m}}^{\mathbf{2}}}\] respectively. If the length         of BC is 4 cm, find the length of EF.

            (a) 5.5 cm                      (b) 4.5 cm

            (c) 6.5 cm                      (d) 7.5 cm

            (e) None of these

Ans.     (c)

Explanation: We know that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their      corresponding sides.

 

            \[\therefore \,\,\text{ }\Delta \,ABC\sim \Delta \,DEF\]

           

           

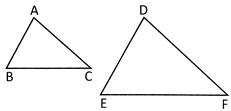
\[\Rightarrow \,\,\,\,\,\,\frac{Area\,(\Delta ABC)}{Area\,(\Delta DEF)}\,\,=\,\,\frac{B{{C}^{2}}}{E{{F}^{2}}}\]

 

\[\Rightarrow \,\,\,\,\frac{64}{169}=\left( \frac{B{{C}^{2}}}{E{{F}^{2}}} \right)\,\,\,\,\Rightarrow \,\,\,{{\left( \frac{8}{13} \right)}^{2}}={{\left( \frac{BC}{EF} \right)}^{2}}\Rightarrow \,\,\,\,\frac{BC}{EF}=\frac{8}{13}\]

 

            \[\Rightarrow \,\,\,\,EF\,\,=\,\,\frac{13}{8}\times BC=\left( \frac{13}{8}\times 4 \right)\,cm\,\,=\,\,6.5\,cm\]

 

4. In the adjoining figure, \[\mathbf{DE}\,\,~\parallel \,\,\mathbf{BC}\], \[\mathbf{AD}\text{ }=\text{ }\mathbf{2}\text{ }\mathbf{cm}\], \[\mathbf{BD}\text{ }=\text{ }\mathbf{2}.\mathbf{5}\text{ }\mathbf{cm}\], \[\mathbf{AE}\text{ }=\text{ }\mathbf{3}.\mathbf{2}\text{ }\mathbf{cm},\text{ }\mathbf{DE}\text{ }=\text{ }\mathbf{4}\text{ }\mathbf{cm}\].

            Determine AC and BC.

 

           

 

          

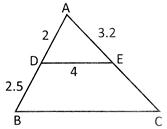
(a) 6.2 cm, 5 cm             (b) 7.2 cm, 9 cm

            (c) 5.2 cm, 9 cm             (d) 6.2 cm, 8 cm

            (e) None of these

Ans.     (b)

            Explanation: In \[\Delta \,ADE\text{ }and\,\,\Delta \,ABC\]:

           

 

                      

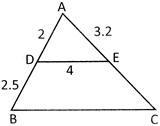
\[\angle \,A\text{ }=\angle \,A\] (common)

                        \[\Delta \,ADE\text{ }-\Delta \,ABC\]

                        (corresponding angles since \[DE\,\,\parallel \,\,~BC\])

                        \[\Delta \,ADE\text{ }\tilde{\ }\Delta \,ABC\]        (AA Similarity)

          

            So,       \[\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}\,\,\,\,\,\,\]                    ……. (i)

           

            From equation (i):

 

\[\frac{AD}{AB}=\frac{AE}{AC}\,\,\,\Rightarrow \,\,\,\frac{2}{4.5}\,\,=\,\,\frac{3.2}{AC}\,\,\Rightarrow \,\,AC=\,\,\left( \frac{3.2\times 4.5}{2} \right)\,cm\,\,=\,\,7.2\,cm\]

 

            Again, form equation (i):

 

\[\frac{AD}{AB}=\frac{DE}{BC}\,\,\,\Rightarrow \,\,\,\frac{2}{4.5}\,\,=\,\,\frac{4}{BC}\,\,\Rightarrow \,\,BC=\,\,\left( \frac{4\times 4.5}{2} \right)\,cm\,\,=\,\,9\,cm\]

 

5. ABC is an isosceles triangle with \[\overline{\mathbf{AB}}\mathbf{ = }\overline{\mathbf{AC}}\mathbf{ = 13 cm}\]. The length of altitude from A on BC is 5 cm. Find \[\overline{\mathbf{BC}}\].

            (a) 24 cm                       (b) 20 cm

            (c) 15 cm                       (d) 25 cm

            (e) None of these

Ans.     (a)

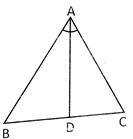
Explanation: In the following figure, Let \[\Delta \,ABC\] be an isosceles triangle having \[AB\text{ }=\text{ }AC\text{ }=\text{ }13\text{ }cm\]. Let      \[AD\bot BC\] and \[AD\text{ }=\text{ }5\text{ }cm\].

 

           

 

          

In \[\Delta \,ABD\]:

            \[A{{B}^{2}}=A{{D}^{2}}+B{{D}^{2}},\,\,\,B{{D}^{2}}=A{{B}^{2}}-A{{D}^{2}}\]

 

\[\Rightarrow \,\,\,BD\,\,\,=\,\,\sqrt{A{{B}^{2}}-A{{D}^{2}}}=\,\,\sqrt{{{13}^{2}}-{{5}^{2}}}=\,\,\sqrt{169-25}\,\,=\,\,\sqrt{144}\,\,=\,\,12\,cm\]

 

            Similarly, \[DC\text{ }=\text{ }12\text{ }cm\].

 

\[\therefore \]      \[BC\text{ }=\text{ }BD\text{ }+\text{ }DC\text{ }=\text{ }\left( 12\text{ }+\text{ }12 \right)\text{ }cm\text{ }=\text{ }24\text{ }cm\].