10th Class Mathematics Triangles

 Triangles

• Similar figures: Two figures having the same shape (not necessarily the same size) are called similar figures.
• Congruent figures: Two figures having the same shape and the same size are called congruent figures.

Note: Congruent figures are similar but similar figures are not congruent.           

• Similar polygons: Two polygons of the same number of sides are similar; if their corresponding angles are equal and their corresponding sides are in the same ratio (or proportion)

Note: The same ratio of the corresponding sides is referred to as the scale factor (or the Representative Fraction) for the polygons.

• Two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional.
• The ratio of any two corresponding sides in two equiangular triangles is always the same.
• Basic Proportionality Theorem; If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides divided in the same ratio.
• Converse of basic proportionality theorem: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
• Criteria for similarity of triangles: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides divided in the same ratio.

Symbol for similarity: \[\sim \]

Symbol forcongruency: \[\cong \]

(a) A.A.A. Similarity: If in two triangles, the corresponding angles are equal and their corresponding sides are proportional, then the two triangles are similar.

Corollary: (AA similarity) If two angles of one triangle are respectively equal to two angles of another triangle, then two triangles are similar.

(b) S.S.S. Similarity: If in two triangles, the sides of one triangle are proportional to the sides of the other triangle, and their corresponding angles are equal, then the triangles are similar.

(c) S.A.S. Similarity: If one angle of and the sides including it of a triangle are proportional to an angle and the sides including it, of another triangle then the two triangles are similar.

• If two triangles are equiangular, then the ratio of their corresponding sides is the same as the ratio of their corresponding (a) medians (b) altitudes and (c) angle bisector segments.
• The ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
• The areas of two similar triangles are in the ratio of the squares of the corresponding altitudes.
• The areas of two similar triangles are in the ratio of the squares of the corresponding angle bisector segments.
• If equilateral triangles are drawn on the sides of a right angled triangle, then the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
• The area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
• If a perpendicular is drawn from the vertex, containing the right triangle to the hypotenuse, then the triangle on each side of the perpendicular is similar to each other and to the original triangle. Also. the square of the perpendicular is equal to the product of the length of the two parts of the hypotenuse.
• Pythagoras' theorem: In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
• Converse of Pythagoras' theorem: In a triangle, if the square on one side is equal to the sum of the squares on the remaining two, the angle opposite the first side is a right angle.
• Results using Pythagoras' theorem:

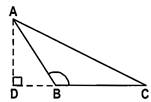
(a) In an obtuse triangle, the square of the side opposite to the obtuse angle is equal to the sum of the squares of the other two sides plus twice the product of one side and the projection of other on first.

In obtuse triangle ABC, Z B is obtuse. If AD BC, then          

\[\text{A}{{\text{C}}^{\text{2}}}=\text{A}{{\text{B}}^{\text{2}}}+\text{B}{{\text{C}}^{\text{2}}}+\text{2(BC)(BD)}\]

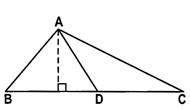
(b) In any triangle, the sum of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of half of the median which bisects the third side.

In A ABC, if AD is the median, the                 

\[\text{A}{{\text{B}}^{\text{2}}}+\text{A}{{\text{C}}^{\text{2}}}=\text{2 }\!\![\!\!\text{ A}{{\text{D}}^{\text{2}}}+\text{B}{{\text{D}}^{\text{2}}}]\]

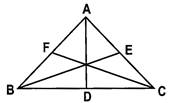
(c) Three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle.

In ABC, with medians AD, BE and CF,        

\[\text{3(A}{{\text{B}}^{\text{2}}}+\text{B}{{\text{C}}^{\text{2}}}+\text{C}{{\text{A}}^{\text{2}}}\text{)}=\text{4(A}{{\text{D}}^{\text{2}}}+\text{B}{{\text{E}}^{\text{2}}}+\text{C}{{\text{F}}^{\text{2}}}\text{)}\]