10th Class Mathematics Introduction to Trigonometry Trigonometric Ratio

 

Trigonometric Ratio

 

 

Trigonometric Ratio

 

1. (i) \[\sin \theta \,\,=\,\,\frac{Perpendicular}{Hypotenuse}\,\,=\,\,\frac{y}{r}\]

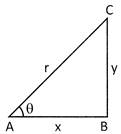
(ii)  \[\cos \theta \,\,=\,\,\frac{Base}{Hypotenuse}\,\,=\,\,\frac{x}{r}\]

            (iii) \[\tan \,\,\theta \,\,=\,\,\frac{Perpendicular}{Base}\,\,=\,\,\frac{y}{x}\]             

(iv) \[\cos ec\,\,\theta \,\,=\,\,\frac{Hypotenuse}{Perpendicular}\,\,=\,\,\frac{r}{y}\]

            (v) \[sec\,\,\theta \,\,=\,\,\frac{Hypotenuse}{Base}\,\,\,=\,\,\frac{r}{x}\]                 

(vi) \[\cot \,\,\theta \,\,=\,\,\frac{Base}{Perpendicular}\,\,\,=\,\,\frac{x}{y}\]

           

2. (i) \[\cos ec\,\,\theta \,\,=\,\,\frac{1}{\sin \,\theta }\,\,\]                             

(ii)  \[sec\,\,\theta \,\,=\,\,\frac{1}{\cos \,\theta }\,\,\]

            (iii) \[\cot \,\,\theta \,\,=\,\,\frac{1}{\tan \,\theta }\,\,\]                               

(iv) \[\tan \,\,\theta \,\,=\,\,\frac{\sin \,\theta }{\cos \,\theta }\,\,\]

            (v) \[\cot \,\,\theta \,\,=\,\,\frac{\cos \,\theta }{\sin \,\theta }\,\,\]

 

3. (i) \[{{\sin }^{2}}+\theta +{{\cos }^{2}}\theta \,\,=\,\,1\,\]

(ii) \[1\,\,+\,\,{{\tan }^{2}}\,\,\theta \,\,=\,\,{{\sec }^{2}}\,\,\theta \,\,for\,\,0{}^\circ \,\,\le \,\,\theta \,\,<\,\,90{}^\circ \]

            (iii) \[1+{{\cot }^{2}}\theta =\cos e{{c}^{2}}\theta \,\,for\,\,0{}^\circ <\theta \le 90{}^\circ \]

 

4. (i) \[sin\,\,\left( 90{}^\circ -\theta \right)=\,\,\cos \,\,\theta \]                      

(ii) \[\cos (90{}^\circ -\theta )\,\,=\,\,sin\theta \]

            (iii) \[\tan (90{}^\circ \,\,-\,\,\theta )\,\,=\,\,cot\theta \]                  

(iv) \[\cot (90{}^\circ \,\,-\,\,\theta )\,\,=\,\,\tan \,\theta \]

            (v) \[\sec (90{}^\circ \,\,-\,\,\theta )\,\,=\,\,\cos ec\,\theta \]

(vi) \[co\sec \,(90{}^\circ \,\,-\,\,\theta )\,\,=\,\,sec\,\theta \]

 

5. The value of sin or cos never exceeds 1, whereas the value of sec or cosec is always greater or equal to 1.

 

6.         Table for T- ratios of \[0{}^\circ ,\text{ }30{}^\circ ,\text{ }45{}^\circ ,\text{ }60{}^\circ ,\text{ }90{}^\circ \]. 

 

\[\theta \]	sin \[\theta \]	cos \[\theta \]	tan \[\theta \]	cosec \[\theta \]	sec \[\theta \]	cot \[\theta \]
\[0{}^\circ \]	0	1	0	not defined	1	not defined
\[30{}^\circ \]	\[\frac{1}{2}\]	\[\frac{\sqrt{3}}{2}\]	\[\frac{1}{\sqrt{3}}\]	2	\[\frac{2}{\sqrt{3}}\]	\[\sqrt{3}\]
\[45{}^\circ \]	\[\frac{1}{\sqrt{2}}\]	\[\frac{1}{\sqrt{2}}\]	1	\[\sqrt{2}\]	\[\sqrt{2}\]	1
\[60{}^\circ \]	\[\frac{\sqrt{3}}{2}\]	\[\frac{1}{2}\]	\[\sqrt{3}\]	\[\frac{2}{\sqrt{3}}\]	2	\[\frac{1}{\sqrt{3}}\]
\[90{}^\circ \]	1	0	not defined	1	not defined	0

 

 

Snap Test

 

1. \[{{(\mathbf{sec}~\theta -\text{ }\mathbf{tan}\theta )}^{\mathbf{2}}}=\] ?

 

            (a) \[\frac{1+\sin \theta }{1-\sin \theta }\]            

(b) \[\frac{2+\sin \theta }{2-\sin \theta }\]

            (c) \[\frac{2-\sin \theta }{2+\sin \theta }\]             

(d) \[\frac{1-\sin \theta }{1+\sin \theta }\]

            (e) None of these

Ans.     (d)

Explanation: \[{{(sec\,\theta -tan\,\theta )}^{2}}\]= \[{{\left( \frac{1-\sin \theta }{\cos \theta } \right)}^{2}}=\frac{{{(1-\sin \theta )}^{2}}}{{{\cos }^{2}}\theta }\,\,=\,\,\frac{{{(1-\sin \theta )}^{2}}}{1-{{\sin }^{2}}\theta }\,\,=\,\,\frac{1-\sin \theta }{1+\sin \theta }\]

 

2. If \[\mathbf{4}\,\mathbf{tan}\,\theta \,\,~=\text{ }\mathbf{3}\], find the value of \[\frac{\mathbf{4}\,\,\mathbf{sin}\theta \,\,\mathbf{-}\,\,\mathbf{2}\,\,\mathbf{cos}\theta }{\mathbf{4}\,\,\mathbf{sin}\theta \,\,\mathbf{+}\,\,\mathbf{3}\,\,\mathbf{cos}\theta }\].

            (a) \[\frac{1}{4}\]           (b) \[\frac{1}{6}\]

            (c) \[\frac{1}{8}\]           (d) \[\frac{3}{8}\]

            (e) None of these

Ans.     (b)

            Explanation: We have \[4\text{ }tan\,\theta \,\,~=\text{ }3\]

            Now,     \[\frac{4\sin \theta \,\,-\,\,2\cos \theta }{4\sin \theta \,\,+\,\,3\cos \theta }\]    =            \[\frac{4\frac{\sin \theta }{\cos \theta }-2}{4\frac{\sin \theta }{\cos \theta }+3}\]

                                                            =         \[\frac{4\tan \theta -2}{4\tan \theta +3}\]

                                                            =         \[\frac{3-2}{3+3}=\frac{1}{6}\].

 

3. If \[\mathbf{tan}\theta \mathbf{=}\frac{\mathbf{a}}{\mathbf{b}}\], then \[\frac{\mathbf{a}\,\mathbf{sin}\theta \mathbf{-b}\,\mathbf{cos}\theta }{\mathbf{a}\,\mathbf{sin}\theta \mathbf{+b}\,\mathbf{cos}\theta }\mathbf{=?}\]

 

(a) \[\frac{{{a}^{2}}\,\,+\,\,{{b}^{2}}}{a\,\,+\,\,b}\]              

(b) \[\frac{{{a}^{2}}\,\,-\,\,{{b}^{2}}}{a{{\,}^{2}}\,-\,\,b}\]

(c) \[\frac{{{a}^{2}}\,\,-\,\,{{b}^{2}}}{{{a}^{2}}\,\,+\,\,{{b}^{2}}}\]                     

(d) \[\frac{{{a}^{2}}\,\,-\,\,{{b}^{2}}}{a\,\,-\,\,b}\]

            (e) None of these

Ans.     (c)

            Explanation: We have \[\tan \theta =\frac{a}{b}\]

            Now, \[\frac{a\,\sin \theta -b\,\cos \,\theta }{a\,\sin \theta +b\,\cos \theta }\] =         \[\frac{a.\frac{\sin \theta }{\cos \theta }-b}{a.\frac{\sin \theta }{\cos \theta }+b}\]

= \[\frac{a\,\tan \theta -b}{a\,\tan \theta +b}\]                 =         \[\frac{a.\frac{a}{b}-b}{a.\frac{a}{b}+b}\]   \[\left[ \therefore \tan \theta =\frac{a}{b}(given) \right]\]

                \[=\frac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}\]

 

4. Evaluate:

\[\mathbf{Si}{{\mathbf{n}}^{\mathbf{2}}}\mathbf{30{}^\circ co}{{\mathbf{s}}^{\mathbf{2}}}\mathbf{45{}^\circ +4ta}{{\mathbf{n}}^{\mathbf{2}}}\mathbf{30{}^\circ +}\frac{\mathbf{1}}{\mathbf{2}}\mathbf{si}{{\mathbf{n}}^{\mathbf{2}}}\mathbf{90{}^\circ -2co}{{\mathbf{s}}^{\mathbf{2}}}\mathbf{90{}^\circ +}\frac{\mathbf{1}}{\mathbf{24}}\]

            (a) 3                              (b) 6

            (c) 4                              (d) 2

            (e) None of these

Ans.     (d)

Explanation: \[si{{n}^{2}}30{}^\circ \text{ }cos+\text{ }45{}^\circ \text{ }+\text{ }4\text{ }ta{{n}^{2}}30{}^\circ \text{ }+\frac{1}{2}\,\,si{{n}^{2}}90{}^\circ \text{ }-\text{ }2\text{ }co{{s}^{2}}90{}^\circ +\frac{1}{24}\]

\[={{\left( \frac{1}{2} \right)}^{2}}\times {{\left( \frac{1}{\sqrt{2}} \right)}^{2}}+4\times {{\left( \frac{1}{\sqrt{3}} \right)}^{2}}+\left( \frac{1}{2} \right)\times {{1}^{2}}-2\times {{(0)}^{2}}+\frac{1}{24}\]

\[=\,\,\left( \frac{1}{4}\times \frac{1}{2} \right)+\left( 4\times \frac{1}{3} \right)+\left( \frac{1}{2}+\frac{1}{24} \right)=\frac{1}{8}+\frac{4}{3}+\frac{1}{2}+\frac{1}{24}\]

                \[=\,\,\frac{3+32+12+1}{24}\,\,=\,\,\frac{48}{24}\,\,=\,\,2\]

 

5. In a \[\Delta \,\mathbf{ABC},\text{ }\mathbf{if}\,\,\angle \mathbf{A}\text{ }=\text{ }\mathbf{30}{}^\circ ,\,\,\,\angle \mathbf{B}\text{ }=\text{ }\mathbf{90}{}^\circ \text{ }\mathbf{and}\text{ }\mathbf{AC}\text{ }=\text{ }\mathbf{10}\text{ }\mathbf{cm}\], then find AB and BC.

            (a) \[5~\sqrt{3}\,cm,\text{ }5\text{ }cm\]            

(b) \[5\sqrt{2}~cm,\text{ }5\text{ }cm\]

            (c) \[5~\sqrt{2}\,cm,\text{ }3\text{ }cm\]            

(d) \[5\sqrt{2}~cm,\text{ }8\text{ }cm\]  

            (e) None of these

Ans.     (a)

Explanation: It is given that in \[\Delta \,ABC\] \[\angle \,A\text{ }=\text{ }30{}^\circ \], and \[AC\text{ }=\text{ }10\text{ }cm\].

            We have:

            (i)    \[\frac{AB}{AC}\text{ }=\text{ }cos\text{ }A\text{ }=\text{ }cos\text{ }30{}^\circ \]

\[\Rightarrow \,\,\frac{AB}{10}=\frac{\sqrt{3}}{2}\Rightarrow AB=\left( 10\times \frac{\sqrt{3}}{2} \right)cm\,\,5\sqrt{3}\,cm.\]

(ii)  \[\frac{BC}{AC}=\sin \,A=\sin 30{}^\circ \,\,\,\,\,\,\Rightarrow \,\,\,\,\,\frac{BC}{10}=\frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\Rightarrow \,\,\,\,BC=\frac{10}{2}\,\,cm\,\,=\,\,5\,cm\]

 

6.         In the given figure, \[\angle \,\mathbf{ABC}=\mathbf{90}{}^\circ ,\,\,\angle \,\mathbf{BAC}=\theta ,\,\,\angle \,\mathbf{ADC}\text{ }=\phi .\text{ }\mathbf{BC}\text{ }=\text{ }\mathbf{5}\text{ }\mathbf{cm},\text{ }\mathbf{AC}\text{ }=\text{ }\mathbf{13}\text{ }\mathbf{cm}\] and \[\mathbf{AD}\text{ }=\text{ }\mathbf{14}\]          cm. Also, \[\angle \,\mathbf{BAD}\text{ }=\text{ }\mathbf{90}{}^\circ \]. Find the values of cosec \[\phi \] and tan\[\phi \]..

                               

           

   

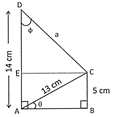
(a) \[\frac{12}{13},\,\frac{4}{3}\]                      

(b) \[\frac{5}{4},\,\frac{4}{3}\]

            (c) \[\frac{4}{3},\,\frac{4}{5}\]              

(d) \[\frac{4}{3},\,\frac{7}{5}\]

            (e) None of these

Ans.     (b)

Explanation: In right \[\Delta \]ABC we have: \[A{{C}^{2}}=\text{ }A{{B}^{2}}+\text{ }B{{C}^{2}}\]

\[\Rightarrow \,\,\,\,\,\,AB\,\,\,\,\,\,\,\,\,\,=\,\,\,\,\,\sqrt{A{{C}^{2}}-B{{C}^{2}}}\,\,\,\,\,=\,\,\,\,\sqrt{{{(13)}^{2}}-{{(5)}^{2}}}\]

                        \[=\,\,\,\,\,\sqrt{169-25}\text{ }=\text{ }\sqrt{144}\text{ }=\text{ }12\text{ }cm.\]

            Now,  \[EC~~~~~~=~~AB\text{ }=\text{ }12\text{ }cm.\]

            and \[DE~~~~~~~~=~~AD\text{ }\text{ }EA\text{ }=\text{ }AD\text{ }-\text{ }BC\]

                                    \[=~~\left( 14\text{ }-\text{ }5 \right)\text{ }cm\text{ }=\text{ }9\text{ }cm.\]      

            In right \[\Delta \,CDE\] we have:

\[C{{D}^{2}}=\text{ }D{{E}^{2}}+\text{ }E{{C}^{2}}=\text{ }{{9}^{2}}+\text{ }{{12}^{2}}=\text{ }81\text{ }+\text{ }144\text{ }=\text{ }225\]

                        \[\Rightarrow \,\,CD=\sqrt{225}=15\,cm.\]

 

                        (i) \[cosec\,\phi \,\,\,\,=\,\,\,\frac{CD}{EC}=\frac{15}{12}=\frac{5}{4}.\]

           

                        (ii) \[\tan \,\phi \,\,\,\,=\,\,\,\frac{EC}{DE}=\frac{12}{9}=\frac{4}{3}.\]

 

7. \[{{\left( \mathbf{cosec}\text{ }\theta \text{ }-\text{ }\mathbf{cot}\text{ }\theta  \right)}^{\mathbf{2}}}\mathbf{is}\text{ }\mathbf{equal}\text{ }\mathbf{to}:\]

 

            (a) \[\frac{2-\,\cos \theta }{1+\cos \,\theta }\]                   

(b) \[\frac{1}{1\,\,-\,\,\cos \theta }\]

            (c) \[\frac{1-\cos \,\theta }{1\,\,+\,\,\cos \,\theta }\]                       

(d) \[\frac{2+\cos \,\theta }{1\,\,+\,\,\cos \,\theta }\]         

 

            (e) None of these

Ans.     (c)                  

Explanation: \[{{\left( cosec\text{ }\theta \text{ }-\text{ }cot\text{ }\theta  \right)}^{2}}={{\left( \frac{1}{\sin \,\theta }-\frac{\cos \,\theta }{\sin \,\theta } \right)}^{2}}={{\left( \frac{1-\cos \theta }{\sin \,\theta } \right)}^{2}}\]

 

            \[=\,\,\,\,\frac{{{(1-\cos \,\theta )}^{2}}}{(1-co{{s}^{2}}\theta )}\]

            \[=\,\,\,\,\frac{{{(1-\cos \,\theta )}^{2}}(1-cos\,\theta )}{(1+cos\theta )(1-cos\theta )}=\frac{1-\cos \,\theta }{1+\cos \,\theta }\]

 

8. \[\frac{\mathbf{sin}\,\,\theta }{\mathbf{1+cos}\,\,\theta }\mathbf{+}\frac{\mathbf{1+cos}\,\,\theta }{\mathbf{sin}\,\,\theta }\,\,\,\mathbf{=}\]

           

            (a) \[2\text{ }cosec\,\theta \]       

(b) \[2\text{ }cos\,\theta \]          

            (c) \[2\text{ }sec\,\theta ~\]                    

(d) \[2\text{ }sin\,\theta \]           

            (e) None of these

Ans.     (a)

Explanation: \[\frac{{{\sin }^{2}}\,\theta }{1+\cos \theta }+\frac{1+\cos \,\theta }{sin\,\theta }=\frac{{{\sin }^{2}}\theta +{{(1+cos\theta )}^{2}}}{\sin \theta (1+cos\,\theta )}\]

 

= \[\frac{{{\sin }^{2}}\theta +{{\cos }^{2}}\theta +1+2\,\cos \theta }{\sin \theta (1+cos\,\theta )}=\frac{2+2\cos \,\theta }{\sin \theta (1+cos\,\theta )}\]

 

= \[\frac{2(1+cos\,\theta )}{\sin \theta (1+cos\,\theta )}=\frac{2}{\sin \,\theta }=2\,\,\cos ec\,\theta \]