10th Class Science Electricity and Circuits Combination of Resistance

       Combination of Resistance

There are two ways of connecting the resistance that is, the series combination and is parallel combination.

Series Combination

The combination, in which the resistance are connected end to end with each other, is called series combination.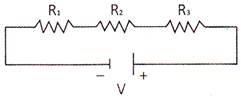 

Let \[{{R}_{1}},\,\,{{R}_{2}}\] and \[{{R}_{3}}\] be three resistance, connected in series across a battery of potential V volt, as shown in the figure above. Now suppose \[{{V}_{1}}\] be the potential difference across the resistance \[{{R}_{1}};\,\,{{V}_{2}}\] be the potential difference across \[{{R}_{2}};\] and \[{{V}_{3}}\] be the potential difference across \[{{R}_{3}}\]. The total potential across the three resistance is given by

\[\mathbf{V=}{{\mathbf{V}}_{\mathbf{1}}}\mathbf{+}{{\mathbf{V}}_{\mathbf{2}}}\mathbf{+}{{\mathbf{V}}_{\mathbf{3}}}\]

But by Ohms law, \[V=I\times R\]

Since the same current I flows through the three resistance \[{{R}_{1}},\,\,{{R}_{2}}\]and \[{{R}_{3}}\], so by ohms law

\[{{V}_{1}}=I\times {{R}_{1}},\,\,{{V}_{2}}=I\times {{R}_{2}}\]and\[{{V}_{3}}=I\times {{R}_{3}}\]

Therefore, \[I\times R=I\times {{R}_{1}}+I\times {{R}_{2}}+I\times {{R}_{3}}\]

\[\Rightarrow \,\,I\times R=I\times \,({{R}_{1}}+{{R}_{2}}+{{R}_{3}})\,\Rightarrow \,\,R={{R}_{1}}+{{R}_{2}}+{{R}_{3}}\]

Hence, the resultant resistance is equivalent to the sum of all individual resistance connected in series.

            Characteristics

• If different resistances are joined with each other in such a way that there is only one path for the flow of electric current, then the combination of such resistances is called Series Combination.
• In series combination current through each resistor is constant.
• In series combination potential difference across each resistor is different depending upon the value of resistance.
• Equivalent resistance of circuit is equal to the sum of individual resistances. The disadvantage of the series combination is that if one component is fused, then the other components of circuit will not function.

          Parallel Combination

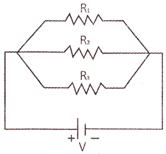
When all the resistance are connected between the two common ends of the circuits, it is called a parallel connection. Let \[{{R}_{1}},\,\,{{R}_{2}}\] and \[{{R}_{3}}\] be the three resistance connected in parallel, as shown in the circuit diagram given above, across a potential difference of V volt. In this case, the potential difference across the ends of all the three resistance will remain same. However the current flowing through each resistance will not be the same. Suppose \[{{I}_{1}},\,\,{{I}_{2}}\] and \[{{I}_{3}}\] be the current flowing through the three resistance \[{{R}_{1}},\,\,{{R}_{2}}\] and \[{{R}_{3}}\] respectively. Then the total current flowing in the circuit is

\[I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}\]

But by Ohm's law, \[I=\frac{V}{R}\]

Therefore, \[{{I}_{1}}=\frac{V}{{{R}_{1}}},\,\,{{I}_{2}}=\frac{V}{{{R}_{2}}}\] and \[{{I}_{3}}=\frac{V}{{{R}_{3}}}\]

Putting these values in the above equation we get,

\[\frac{V}{R}=\frac{V}{{{R}_{1}}}+\frac{V}{{{R}_{2}}}+\frac{V}{{{R}_{3}}}\]

\[\Rightarrow \,\frac{V}{R}=V\,\left( \frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}} \right)\]                \[\Rightarrow \,\,\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}\]

Hence the equivalent resistance is equal to the sum of reciprocal of individual resistance.

         Characteristics

• If there are more than one path for the flow of current in a circuit then the combination of resistances is called Parallel Combination.
• In parallel combination current through each resistor is different.
• Potential difference across each resistor is constant.
• Equivalent resistance of circuit is always less than either of the resistances included in the circuit.

Note: The main advantage in parallel combination of resistors is that if one component of circuit is damaged, the rest of the component of the circuit will perform their work without any disturbance. It is due to the presence of more than one path for the flow of electric current.

            a  Factors Affecting the Resistance of a Conductor

The factor on which the resistance of the conductor depends are the length of the conductor, area of cross section, nature of material and temperature of the conductor.

              Effect of Length of Conductor

If we increase the length of the conducting wire, its resistance increases. On the other hand, if we decreases the length of the wire, the resistance of the conductor decreases. Thus, we conclude that the resistance of the conductoris directly proportional to the length of the conductor, if we double the length of the wire, the resistance of the wire gets doubled and if we reduce the length of the wire to half, the resistance get reduced to half.

            Effect of Area of Cross Section

The resistance of the wire is inversely proportional to the area of the cross section of the wire. So if we double the area of the cross section of the wire, the resistance get reduced to half. But if we reduce the area of cross section of the wire to half the resistance get doubled. Thus, we can say that thinner is the wire more is the resistance and thicker is the wireless is the resistance.

            Effect of Nature of Material

The resistance of the wire also depends on the nature of material. Some material have low resistance and are called the good conductor. Some have high resistance and are considered bad conductors.

           Effect of Temperature

The resistance of the pure metal increases with increase in temperature and decreases with the decrease in temperature. But for alloy the resistance is almost remains unaffected with the temperature. The wire such as copper and aluminium are used for transmission of electricity because they have low resistivity. On the other hand alloy such as nichrome are used as a heating element in toaster, electric iron, etc, because the resistivity of the alloy is very high and does not undergo oxidation easily even at high temperature.