10th Class Science Light - Reflection and Refraction Lens

      Lens

A transparent object having two refracting surface is called lens. It is of two types, concave lens and convex lens. Working of lens is based on the refraction of light passing through it.

           Convex Lens

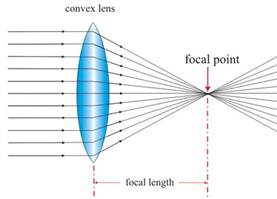
Convex lens is the lens which is thicker at the center and thinner at the edge. It has two refracting surfaces. It is also called the converging lens as the ray of light converges at a point after refraction. The point, at which ray of light converges after refraction, is called the focus of the lens.

           Concave Lens

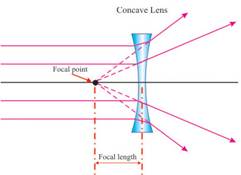
It is the lens which is thinner at the center and thicker at the edge. It also has two refracting surfaces. It is called diverging lens as the ray of light diverges in different direction after refraction.

The centre of the lens is called the optical center. It is normally denoted by C. The ray of light passing through optical center do not undergo any’ deviation, and goes in a straight line. Thus, the line passing through the optical center of the lens and perpendicular to both the face of the lens, is called the principal axis. The ray of light that converges at a point on the principal axis is known as the principal focus. The distance between focus and optical centre is called the focal length.

            Image Formation by a Convex Lens

I. When the object is at infinity

Properties of Image formed is

1. Image is formed at focus.
2. Image is real and inverted.
3. Highly diminished.

II. When the object is beyond \[2{{F}_{1}}\]

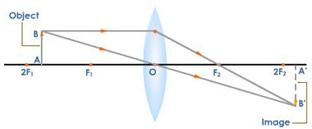
Properties of Image formed is  

1. Image is formed between \[{{F}_{2}}\] and \[2{{F}_{2}}\].
2. Image is real and inverted.
3. Image is diminished.

III. When the object is at \[2{{F}_{1}}\]

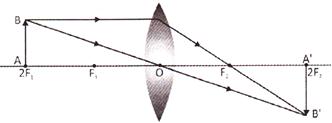
Properties of Image formed is

1. Image is formed at \[2{{F}_{2}}\].
2. Image is real and inverted.
3. Image is equal in size to that of the object.

1. When the object is between \[2{{F}_{1}}\] and \[{{F}_{1}}\]

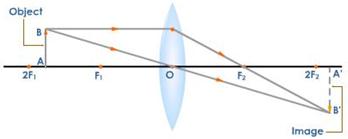
Properties of Image formed is

1. Image is formed beyond \[2{{F}_{2}}\].
2. Image is real and inverted.
3. Image is larger in size to that of the object.

V. When the object is at \[{{F}_{1}}\]

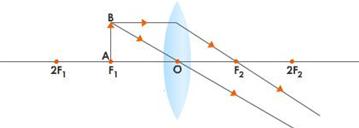
Properties of Image formed is

1. Image is formed infinity
2. Image is real and inverted.
3. Image is highly enlarge.

VI. When the object is \[{{F}_{1}}\]is between optical centre

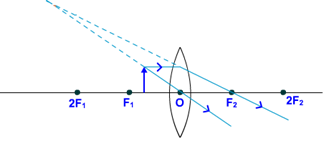
Properties of Image formed is

1. Image is formed behind object.
2. Image is virtual and erect.
3. Image is enlarged.

The summary of the above observation is given in the table below:

           Image Formation by a Concave Lens

When the objects at any point between optical center and infinity

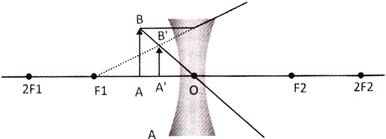
Properties of Image

A. Image is formed between 0 and P.

B. Image is Virtual and Erect.

C. Smaller is size.

          Uses of Concave Lens

• It is used for correcting myopia.
• Along with convex lens it can be used for correction of spherical aberration and chromatic aberration, and chromatic aberration.
• It is used in binoculars.

             Uses of Convex Lens

• It is used as a magnifying glass.
• It is used for correcting hypermetropia defects in eyes.
• It is also used in microscope and reflecting telescope.

             Sign Convention used in Lens

• For convex lens the object distance is negative, as it is to the left of thelens. The image distance and focal length is positive for all real image, as it is to the right of the lens.
• For virtual image the image distance is negative, as it is formed behind the object and to the left of the lens.
• For concave lens the object distance, image distance and focal length are all negative, as all of them lie to the left of the lens.

           Lens Formula

The mathematical relationship between the object distance, image distance, and focal length is called the lens formula. It is expressed as;

\[\frac{1}{f}=\frac{1}{v}=\frac{1}{u},\]where, f is the focal length, v is the image distance and u is the object distance.

Magnification of the lens is defined as the ratio of height of image to theheight of object or ratio of image distance to the object distance. It is expressed as:

\[m=\frac{v}{u}=\frac{{{h}_{2}}}{{{h}_{1}}}\]