Notes - Mathematics Olympiads - Continuity Differentiability
Category : 11th Class
Continuity and Differentiability of a Function
Introduction
The word 'continuous' means without any break or gap. If the graph a function has no break or gap or jump, then it is said to be continuous. A function which is not continuous is called a discontinuous function. While studying graphs of functions, we see that graphs of functions sinx, x, cosx, etc. are continuous on R but greatest integer functions [x] has break at every integral point, so it is not continuous. Similarly tanx, cotx, seex, 1/x etc. are also discontinuous function on R.
Continuous Function
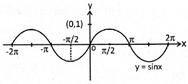
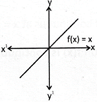
Discontinuous Function


Continuity of a Function at a Point
A function f(x) is said to be continuous at a point x = a of its domain if and only if it satisfies the following three condition:
(i) f(a) exist. ('a' line in the domain of f)
(ii) \[\underset{x+a}{\mathop{\lim }}\,\] f(x) exist e.e; \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\] f(x)= \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\] f(x) or R.H.L= L.H.L
(iii) \[\underset{x+a}{\mathop{\lim }}\,\] f(x) = f(a) (limit equals the value of function)
Continuity from Left and Right
A function f(x) is said to be continuous at a point x = a of its domain if and only if it satisfies the following three condition:
(i) f(a) exist. ('a' line in the domain of f)
(ii) \[\underset{x+a}{\mathop{\lim }}\,\] f(x) exist e.e; \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\] f(x)= \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\] f(x) or R.H.L= L.H.L
(iii) \[\underset{x+a}{\mathop{\lim }}\,\] f(x) = f(a) (limit equals the value of function)
Cauchy's Definition of Continuity
A function f is said to be continuous at a point a of its domain D if for every \[\varepsilon >o\] there exists \[\delta >o\] (dependent of\[\varepsilon \]) such that \[\left| x-a \right|<\delta \]
\[\Rightarrow \left| \text{f}(x)-\text{f(a)} \right|<\varepsilon \]
Comparing this definition with the definition of limit we find that f(x) is continuous at x = a if \[\underset{x\to a}{\mathop{\lim }}\,\]f(x) exists and is equal to f(a) i.e; \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\] f(a) \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\] f(x).
Continuity from Left and Right
Function f(x) is said to be
(i) Left continuous at x= a if \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\,\,\text{f(x)=f(a)}\text{.}\]
(ii) Right continuous at x = a if \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\,\,\text{f(x)=f(a)}\text{.}\]
Thus a function f(x) is continuous at a point x = a if it is left continuous as well as right continuous at x = a.

Differentiation
The function, f(x) is differentiable at point P, iff there exists a unique tangent at point P. In other words, f(x) is differentiable at point P iff the curve does not have pas a corner point i.e; the function is not differentiable at those point on which function has jumps (or holes) and sharp edges.
Let us consider the function \[\text{f(x)=}\left| x-1 \right|,\]which can be graphically shown.
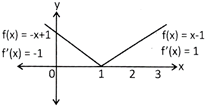
Which show f(x) is not differentiable at x = 1. since f(x) has no edge at x=1.
(i) Right hand derivative: R.H.D. of f(x) at x= a. denoted by
\[\text{f }\!\!'\!\!\text{ (a+o)=f }\!\!'\!\!\text{ }({{a}^{+}})=\underset{h\to o}{\mathop{\lim }}\,\frac{\text{f(a+h)-f(a)}}{h}\]
(ii) Left hand derivative: L.H.D. of f(x) at x= a, denoted by
\[\text{f }\!\!'\!\!\text{ (a-o)=f }\!\!'\!\!\text{ }({{a}^{-}})=\underset{h\to o}{\mathop{\lim }}\,\frac{\text{f(a-h)-f(a)}}{-h}\]
(iii) A function f(x) is said to be differentiable (finitely) at x = a.
if \[\text{f }\!\!'\!\!\text{ (a+o)=f }\!\!'\!\!\text{ }(a-o)=\] finite
\[\Rightarrow \underset{h\to o}{\mathop{\lim }}\,\frac{\text{f}(a+h)-f(a)}{h}=\underset{h\to o}{\mathop{\lim }}\,\frac{\text{f}(a-h)-f(a)}{-h}=\] finite and the common limit is called the derivative of f(x) at x=a. denoted by \[f'(a)\].
\[\Rightarrow \text{f }\!\!'\!\!\text{ (a)=}\underset{h\to a}{\mathop{\lim }}\,\frac{f(x)-f(a)}{x-9}\] {\[x\to 9\] from the left as well as from the right}.
Sol: \[y=\text{f}(x)=sinx\] .....(1)
Let \[\delta \times \] be the small increasement in \[\times \] then \[\delta y\] be the corresponding increasement in y.
\[y=\delta y=sin(x+\delta x)\] …..(2)
Now (2)-(1), we have
\[y+\delta y-y=sin(x+\delta x)-sinx\]
\[\delta y=2.\cos \frac{x+\delta x+x}{2}.\sin \left( \frac{x+\delta x-x}{2} \right)\]
Dividing dx on both sides and taking limit \[\delta x\to 0,\] we have
\[\underset{\delta x\to 0}{\mathop{\lim }}\,\frac{\delta y}{\delta x}=\underset{\delta x\to 0}{\mathop{\lim }}\,2.\frac{\cos \left( \frac{2x+\delta x}{2} \right).\sin \left( \frac{\delta x}{2} \right)}{\delta x}\]
\[\frac{dy}{dx}=\underset{\delta x\to 0}{\mathop{\lim }}\,2.\cos \left( x+\frac{\delta x}{2} \right).\left( \frac{\sin \frac{\delta x}{2}}{\frac{\delta x}{2}\times 2} \right)\]
Applying limit \[\delta x\to 0=\cos x\times 1=\cos x\left[ \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \theta }{\theta }=1 \right]\]
i.e. \[\frac{d}{dx}(\sin x)=\cos x\]
\[\frac{dy}{dx}\]is said to be differential coefficient of y = f(x).
It is denoted by \[{{y}_{1}}=\frac{dy}{dx}=\text{f }\!\!'\!\!\text{ (x)}\]
e.g. \[\frac{d}{dx}(5{{x}^{2}})=5.\frac{d}{dx}({{\underline{x}}^{2}})\]
\[=.5.2.{{(x)}^{2-1}}=10{{x}^{1}}=10x\]
\[={{e}^{x}}.\frac{d}{dx}(\sin x)+\sin \frac{d}{dx}({{e}^{x}})={{e}^{x}}\cos x+\sin x\,\,{{e}^{x}}={{e}^{x}}(\cos x+\sin x)\]
\[=\frac{\sin x\frac{d}{dx}({{\underline{x}}^{2}})-{{x}^{2}}\frac{d}{dx}(\sin x)}{{{\sin }^{2}}x}\]
\[=\frac{d}{dx}({{\log }_{c}}{{a}^{x}})-\frac{d}{d{{x}_{({{a}^{x}})}}}(\log {{a}^{x}}).\frac{d}{dx}({{\underline{a}}^{x}})=\frac{1}{{{a}^{x}}}.{{a}^{x}}.\log a=\log a\]
You need to login to perform this action.
You will be redirected in
3 sec
