Standing Waves or Stationary Waves
Category : JEE Main & Advanced
When two sets of progressive wave trains of same type (both longitudinal or both transverse) having the same amplitude and same time period/frequency/wavelength travelling with same speed along the same straight line in opposite directions superimpose, a new set of waves are formed.
These are called stationary waves or standing waves.

In practice, a stationary wave is formed when a wave train is reflected at a boundary. The incident and reflected waves then interfere to produce a stationary wave.
(1) Suppose that the two super imposing waves are incident wave \[{{y}_{1}}=a\sin (\omega \,t-kx)\] and reflected wave \[{{y}_{2}}=a\sin (\omega \,t+kx)\]
(As \[{{y}_{2}}\] is the displacement due to a reflected wave from a free boundary)
Then by principle of superposition
\[y={{y}_{1}}+{{y}_{2}}=a\,[\sin \,(\omega \,t-kx)+\sin (\omega \,t+kx)]\]
(By using sin \[\sin C+\sin D=2\sin \frac{C+D}{2}\cos \frac{C-D}{2}\])
\[\Rightarrow \] \[y=2a\cos kx\,\sin \omega \,t\]
(If reflection takes place from rigid end, then equation of stationary wave will be \[y=2a\sin kx\,\cos \omega \,t\])
(2) As this equation satisfies the wave equation
\[\frac{{{\partial }^{2}}y}{\partial {{t}^{2}}}={{v}^{2}}\frac{{{\partial }^{2}}y}{\partial {{x}^{2}}}\]. It represents a wave.
(3) As it is not of the form \[f(ax\pm bt),\] the wave is not progressive.
(4) Amplitude of the wave \[{{A}_{SW}}=2a\cos kx.\] Amplitude in two different cases
| Reflection at open end | Reflection at closed end |
| \[{{A}_{SW}}=2a\cos kx\] | \[{{A}_{SW}}=2a\sin kx\] |
|
Amplitude is maximum when \[\cos \,kx=\pm 1\] \[\Rightarrow \] \[kx=0,\,\,\pi ,\,\,2\pi ,\,\,...\,\,n\pi \]. \[\Rightarrow \] \[x=0,\,\frac{\lambda }{2},\,\lambda \,.......\frac{n\lambda }{2}\] where \[k=\frac{2\pi }{\lambda }\] and n = 0, 1, 2, 3, ... |
Amplitude is maximum when \[\sin \,kx=\pm 1\] \[\Rightarrow \] \[kx=\frac{\pi }{2},\,\frac{3\pi }{2}\,.....\frac{(2n-1)\pi }{2}\] \[\Rightarrow \]\[x=\frac{\lambda }{4},\frac{3\lambda }{4}.......\] where \[k=\frac{2\pi }{\lambda }\]and n = 1, 2, 3, .... |
|
Amplitude is minimum when \[\cos kx=0\] \[\Rightarrow \]\[kx=\frac{\pi }{2},\,\frac{3\pi }{2}\,.....\frac{(2n-1)\pi }{2}\] \[\Rightarrow \] \[x=\frac{\lambda }{4},\frac{3\lambda }{4}.......\] |
Amplitude is minimum when \[\sin kx=0\] \[\Rightarrow \] \[kx=\frac{\pi }{2},\,\frac{3\pi }{2}\,.....\frac{(2n-1)\pi }{2}\] \[\Rightarrow \] \[x=0,\,\frac{\lambda }{2},\,\lambda \,.......\frac{n\lambda }{2}\] |
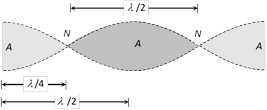
(5) Nodes (N) : The points where amplitude is minimum are called nodes.
(i) Distance between two successive nodes is \[\frac{\lambda }{2}\].
(ii) Nodes are at permanents rest.
(iii) At nodes air pressure and density both are high.
(6) Antinodes (A) : The points of maximum amplitudes are called antinodes.
(i) The distance between two successive antinodes is \[\frac{\lambda }{2}\]
(ii) At nodes air pressure and density both are low.
(iii) The distance between a node (N) and adjoining antinode (A) is \[\frac{\lambda }{4}\].
You need to login to perform this action.
You will be redirected in
3 sec
