Geometrical Figures
Category : 2nd Class
Geometrical Figures
Line
Let's see the lines given below:

Give the name of all slant lines from the figure given below.
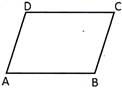
(a) AD and BC (B) AB and BC
(c) AB and AD (D) All the above
(e) None of these
Answer (a)
Which one of the following is correct about the line?
(a) A straight line is measured by ruler.
(b) A straight line cannot be measured by ruler.
(c) A straight line is measured in grams.
(d) All the above
(e) None of these
Answer (a).
Note: We use ruler to measure a straight line.
Angle
An angle is formed at the meeting point of two lines or an angle is formed when two lines meet. The point where two lines meet is called vertex. See the figures given below:
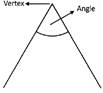
Which one of the following is correct about the angle?
(a) Both sides of an angle must be equal in length
(b) Both sides of an angle may be unequal in length
(c) Two lines cannot form an angle
(d) Three lines are required for formation of an angle
(e) None of these
Answer (b)
Which one of the following is representing an angle?
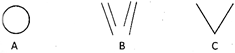
Answer (c)
Note: Both the sides of an angle may be unequal in length.
Square
A square has four equal sides and four equal angles.
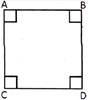
In this picture side AB = BD = CD = AC
And \[\angle A=\angle B=\angle C=\angle D=90{}^\circ \]
If the sum of three angles of a square is\[270{}^\circ \], then the measurement of its fourth angle will be?
(a) \[70{}^\circ \] (b) \[80{}^\circ \]
(c) \[90{}^\circ \] (d) All the above
(e) None of these
Answer (c)
Explanation: Each angle of the square is\[90{}^\circ \].
Quadrilateral
Properties
A quadrilateral has:
The following are the quadrilaterals:
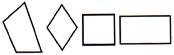
A plane figure has four sides and four vertices. The name of the plane figure is:
(a) Quadrilateral (b) Triangle
(c) Pentagon (d) All the above
(e) None of these
Answer (a)
Rectangle
Properties
In a rectangle:
See the figure given below:
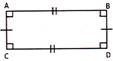
Here,
AB = CD
And AC = BD
\[\angle A=\angle B=\angle C=\angle D=90{}^\circ \]
Similarly

Which one of the following is correct about a rectangle, if a pair of opposite sides is PQ and RS, another pair of opposite sides is PS and QR?
(a) \[PQ\ne RS\,\,and\,\,PS=QR\]
(b) \[PQ=RS\,\,and\,\,PS=QR\]
(c) \[PQ=PS=RS=QR\]
(d) All of these
(e) None of these
Answer (b)
Explanation: Opposite sides of a are rectangle are equal.
Note: A rectangle is a quadrilateral.
Rhombus
Properties
In a rhombus:
See the figure given below:
Here, the sides
AB = BC = CD = AD
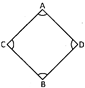
Which one of the following differentiates the rhombus and square?
(a) Rhombus has all equal sides
(b) Rhombus has all unequal sides
(c) Each angle of a rhombus may not be a right angle
(d) All the above
(e) None of these
Answer (c)
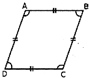
Parallelogram
Properties
In a parallelogram:
See the parallelogram given below
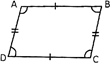
Here, the sides AB = CD & AB | | CD
AD= BC & AD | | BC.
And the opposite angles, \[\angle A=\angle C\,\,\And \,\,\angle B=\angle D\]
You need to login to perform this action.
You will be redirected in
3 sec
