2nd Class Mathematics Multiplication Multiplication and Division

Multiplication and Division

 

Multiplication by Repeated Addition

Multiplication is the repeated addition. Multiplication of 5 and 4 is written as 5 \[\times \] 4 = 5 + 5 + 5 + 5 = 20. Let?s understand this through an example:

 

•          Example:

There are two paper boxes of oranges each contains 24 oranges. How many oranges are there in all?

24 \[\times \] 2 = 24 + 24 = 48. Therefore, total oranges in both the boxes will be 48.

 

Multiplication of Two Numbers

The following are the steps for the multiplication of two numbers. For example multiply 12 and 2.

 

Step I:

Write down the numbers to be multiplied in columns as shown below:

 

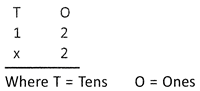
Step II:

Multiply ones as below:

2 Ones \[\times \] 2 = 4 Ones

It is written as:

 

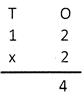
Step III:

Multiply tens as shown below:

1 tens \[\times \] 2 = 2 tens

            Write 2 under tens column.

            \[\begin{matrix}

   T & O  \\

   1 & 2  \\

   \times  & 2  \\

   {} & 4  \\

\end{matrix}\]

 

Therefore the product of 12 and 2 = 24

 

Multiplication of Three Numbers

 

•          Example:

5 \[\times \] 2 \[\times \] 4 = 40

 

Trick:

1st multiply any two numbers and then multiply the result with the remaining number.

                  Now first multiply  5 and 2 thus \[5\times 2=10\]

                  and then \[10\times 4=40\]

 

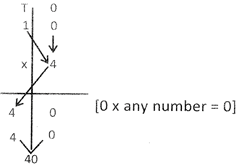
Word Problems

Let?s see the examples given below:

 

•          Example:

An egg tray contains 12 eggs. How many trays are required for 36 eggs?

Trick:

1 tray contains 12 eggs

2 trays contain 2 \[\times \] 12 = 24 eggs             

3 trays contain 3 \[\times \] 12 = 36 eggs

 

•          Example:

A factory produces 15 items in a day. How many items it will produce in a week if Sunday is a holiday?

 

Trick:

Items produced in a day = 15

Items produced in 6 days = 15 \[\times \] 6 = 90 items.

 

Finding Cost of Various Items

Let?s see the examples given below:

 

•          Example:

If the cost of onions is ` 10 per kg, what is the cost of 5 Kg onions?

 

Trick:

To solve the problem, multiply the quantity of onions with its cost.

Hence, required cost = Quantity of onions \[\times \] The cost of one kg of onions. 5 \[\times \] 10 = Rs. 50

 

Multiplication Series

To solve the problems based on multiplication series, we require to remember tables of numbers.

Observe the following multiplication series and fill the blank with correct number: 4, 12, 20, _______, 36

First number is 4 and second number is obtained by multiplying 4 \[\times \] 3 = 12, third number is obtained by multiplying 4 \[\times \] 5 = 20, hence, the fourth number obtained by multiplying 4 \[\times \] 7 = 28

 

•           Example:

Fill in the blank with suitable number

7, 14, 21, ___, 35, 42

(a) 30                                                                (b) 35

(c) 28                                                                (d) 42

(e) None of these            

Ans.     (c)

Explanation: Series goes as 7 \[\times \] 1, 7 \[\times \] 2, 7 \[\times \] 3, 7 \[\times \] 4, 7 \[\times \] 5, 7 \[\times \] 6. Therefore, option (c) is correct.

 

Division

Division means equal distribution.

 

Facts About Division

(i) Division is repeated subtraction.

(ii) Division is inverse of multiplication,

(iii) The symbol of division is horizontal line and two dots (-).

(iv) The number which gets divided is called the DIVIDEND, denoted by capital ?D?

(v) The number which divides the dividend is called the DIVISOR, denoted by ?d?

(vi) The number which tells us how many times the division has been carried out is called the QUOTIENT, denoted by ?Q?.

(vii) The number which is left after the division is called the REMAINDER, denoted by ?R?

(viii) The division should be continued till the remainder is either ?0? or less than the divisor (d).

(ix) A number divided by 1 gives the number itself as the quotient.

(x) A number divided by itself gives 1 as the quotient.

(xi) Zero divided by any number gives 0 as the quotient.

 

Division by Grouping Equally

•           Example:

How much will you get if 12 pencils are equally divided between you and your friend?

By grouping 12 pencils into two equal groups.

 

            6 pencils                                                6 pencils

Therefore, you get 6 pencils and your friend gets 6 pencils.

Division by Repeated Subtraction

 

•           Example:

15 \[\mathbf{\div }\] 3 = 5

We can divide 15 cakes equally among 3 children by repeated subtraction.

Give 5 cakes to first child. 10 cakes are left.

Give 5 cakes to second child then 5 cakes are left.

Give 5 cakes to third child then, no cake is left.

 

Short Division

•           Example:

Divide 27 by 3.

            Step 1: To divide 27 by 3 by short division method we write

            Step 2: Then recite the table of 3 till you come to 27 i.e. 3 \[\times \] 9= 27.

            Therefore  

Or, 27 \[\div \] 3 = 9.

 

            Here, Dividend   =         27,        Divisor         =     3

            Quotient            =         9,         Remainder   =     0

 

Long Division

Divide 859 by 7.

            Start with the hundreds.

           

 

            The process of division is same in long divisions, as discussed in short division,

            Here, Dividend =

            Divisor         =  

            Quotient       =

            Remainder     =

 

Division by 10

If the divisor is 10 then the digit at the one?s place of the dividend is the remainder (R) and the number formed by the remaining digits of the dividend will be the quotient (Q).

 

•          Example:

68 \[\mathbf{\div }\] 10

Unit place is 8 hence, 8 is the remainder and remaining digit of the dividend 6 is quotient,

 

Division by 100

If the divisor is 100 then the number formed by the last two digits from right of the dividend will be the remainder (R) and the number formed by the remaining digits of the dividend will be the quotient (Q).

 

•          Example:

3421 \[\mathbf{\div }\] 100

In the above division, the last two digits from right of the dividend is 21. Hence, the remainder = 21.

The number, which is formed by the remaining digit is the quotient. Thus, quotient = 34.

 

Division by 1000

If the divisor is 1000 then the number formed by the last three digits of the dividend will be the remainder (R) and the number formed by the remaining digits of the dividend will be the quotient (Q).

 

•          Example:

434567 \[\mathbf{\div }\] 1000

In the above division the number which is formed by the last three digits of the dividend is 567. Hence, the remainder = 567 and quotient = 434.

 

Verification of Division

Dividend = Divisor \[\times \] Quotient + Remainder.

 

•          Example:

Divide 87 by 7 and verify the division.

 

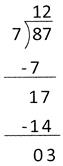
Here,

            Dividend            =         \[[\,87\,]\]

            Divisor               =         \[[\,7\,]\]

            Quotient            =         \[[\,12\,]\]          

            Remainder         =         \[[\,3\,]\]

            Verification: Dividend = Divisor \[\times \] Quotient + Remainder.

            Or \[[\,87\,]\]                  =         \[[\,7\,]\times [\,12\,]+[\,3\,]\]

                                    =         \[[\,84\,]+[\,3\,]\]

                                    =         \[[\,87\,]\] (Dividend)

 

Word Problems

•          Example:

There are 56 articles. How many groups of articles can be made, if each group contains 8 articles?

Ans.     7 groups

Explanation: The total number of groups, if each contains 8 article = 56 \[\mathbf{\div }\] 8

           

 

•          Example:

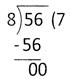
If a bus can carry 45 children, then find the total number of buses required to carry 360 children.

Ans.     8 buses

Explanation: Total number of children is divided by capacity of one bus = 360 \[\mathbf{\div }\] 45 = 8 buses