3rd Class Mathematics Fun with Numbers-973 Fun with Numbers

Learning Objectives

This lesson will help you to read:—

• understand even and odd number.
• understand ascending and descending order.
• know about place value, face value expanded form of numbers and number names.
• learn about smallest and largest number.
• understand skip counting.

Amazing Facts

Zero (0) is the only number which cannot be represented by Roman numerals.

Abacus is considered the origin of the calculator.

While writing number names from 0 to 1,000 the letter “A” only appears in 1,000 (‘’ one thousand ’)

Quick Concept Review

Even and odd Numbers

• Numbers which are divisible by 2 are called even numbers. Examples: 2, 4, 6 etc.
• Numbers which are not divisible by 2 are called odd numbers. Examples: 3, 5, 7 etc.

Ascending and Descending Numbers

• Arranging numbers in ascending order means arranging them from smaller to greater.
• Arranging Numbers in descending order means arranging them from greater to smaller.
• Let the series of numbers be 30,12,18,17, 22, 48, 40, and 28.
• Ascending order of these numbers is 12, 17, 18, 22, 28, 30, 40, 48
• Descending order of these numbers is 48, 40, 30, 28, 22, 18, 17, 12

Place Value

The value of a digit due to its position in a number is called its place value.

For example if we have to place 87654 we will show it        

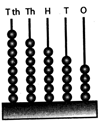
Face Value

Face value of a digit in a number is the digit itself. For example- Face value of 9 in 1892 is 9.

Let's understand the concept of place value and face value with few more examples.

• For a 5-digit number 87654:
• Place value of 4 = 4 ones = 4, Face value of 4 = 4
• Place value of 5 = 5 tens = 50, Face value of 5 = 5
• Place value of 6 = 6 hundreds = 600, Face value of 6 =6
• Place value of 7=7 thousands = 7000, Face value of 7 =7
• Place value of 8 = 8 ten thousands = 80000, Face value of 8 = 8

Expanded Form of Number

We find that when we add the place values of all the digits in a number we get the number. For example:-

300 +80+6 is the expanded form of 386.

Let's get it clear with few more examples:

(a) 819 = 800+10+9

(b) 206 =200+6

(c) 467 = 400 +60+7

Number Names

We know that a number's name is derived from where the digits are placed in the number. For example: The number name of 87654 is Eighty seven thousand six hundred and fifty four.

Few more examples for you:

(a) 32436 –Thirty two thousand four hundred and thirty six.  

(b)  126252 – Twelve thousand six hundred and fifty two

Historical preview

• The first true written positional numeral system is considered to be the Hindu Arabic numeral system. This was established by the 7^th

 Smallest and Largest Number

• Number which is largest in a given series of numbers is known as largest or greatest number.
• Number which is smallest in a given series of numbers is known as smallest number
• Let the series of numbers be 12, 18, 22, 24, 40, and 38. In this, 40 is the greatest largest number and 12 is the smallest number

Let's take another example.

Also look at these examples of greater than and less than.

(a) Greater than:              43 > 34

(b) Less than:                     57 < 69

(c) Equal to:                        197 = 197

Skip Counting

• In skip counting, value of the numbers increase uniformly
• skip counting of 2 can be done as -

2, 4, 6, 8, 10....

(b) skip counting of 3 can be done as - 3,6,9,12,15....

(c) Skip count in fives following 50 can be done as 55, 60, 65, 70....

 Here, every number is five number more than the previous number