Division
Category : 4th Class
LEARNING OBJECTIVES
This lesson will help you to:—
Real Life Example
Division is used in almost and every sphere of our life. Division is used in daily household activities, shopping in a mall, eating pizza etc.
QUICK CONCEPT REVIEW
What is DIVISION?
Division is splitting into equal parts or groups.
It is the result of "fair sharing".
When we share equally we divide.
Symbolically, we write it as follows;
\[27\div 9=3\]
For example:

Kitty found 25 beautiful pearls on the seashore. She collected and brought all of them home. Now she wants to put them in jewellery boxes. She can put 5 pearls in one jewellery box.
She made 1 group of 5 pearls & put them in 1 jewellery box.

She put 5 more pearls in 2nd jewellery box.

She is left with some pearls, so she put 5 pearls in another jewellery box.

5 more in another jewellery box.

5 pearls in another box.

There are no more pearls left.
Kitty required 5 jewellery boxes to keep the pearls.
Therefore, we can say that 25 pearls put into equal groups of 5 each gives 5 groups.
OR
We can say that, 25 pearls divided by 5 pearls in 1 group gives 5 groups.
When we group equally, we divide.
Symbolically, we write it as,
\[25\div 5=5\]
Hence. Division is splitting into equal parts or groups.
It is separating or distributing something into parts
Amazing Facts
The remainder must always be smaller than the divisor.
You can check the answer by just following a simple rule –
\[\left( \text{QUOTIENT }\!\!\times\!\!\text{ DIVISOR} \right)\]
+ REMAINDER = DIVIDEND
Any number divided by 10 gives the ones digit as remainder as the other digits as the quotient.
TERMINOLOGY
Dividend
The number to be divided is called the dividend. It is the number you want to divide up.
For example:\[12\div 6=2\]. Here 12 is to be divided by 6.
Hence, 12 is the dividend.
Divisor
The number which divides the dividend is called the divisor. It is the number that we are dividing by. For example:\[12\div 6=2\]. Here 12 is to be divided by 6.
Hence, 6 is the divisor.
Quotient
The result obtained after dividing one number by another is called quotient. It is the answer in division. For example:\[12\div 6=2\]. Here 12 divided by 6 gives 2.
Therefore, 2 is the quotient.
PROPERTY OF DIVISION
Zero Property
(a) If zero is divided by any number, the answer is always zero.
For example: if we have zero number of chocolates to be divided amongst the students, then each will get zero chocolate.
\[0\div 5=0\]
(b) If any number is divided by zero, then problem cannot be solved.
Property of one
If any number is divided by one, the answer is the number itself.

For example: Ram's family has gone to the market so he is alone at home. There are 9 cookies kept in the kitchen. How many cookies will Ram get to eat?
Here, Ram can eat all the 9 cookies as there is no one else to share the cookies.
Therefore, 9 cookies are to be divided amongst 1 person.
That is, \[9\div 1=9\]
Dividing a number by itself
If any number is divided by itself, the answer will always be one.

For Example: Ram's family is back at home. They have brought pizza for all of them. There are total 6 members in the family including Ram. The pizza is divided in 6 equal parts. How many parts will each member get?
6 equal parts are to be shared amongst 6 members.
That is,\[6\div 6=1\].
Each member will get 1 part of pizza.
Therefore, we can say that any number divided by itself gives 1 as the quotient.
LONG DIVISION
Division can also be shown as follows:
\[Divisor\overset{Quotient}{\overline{\left){Dividend}\right.}}\]
For example: \[9\div 3=3\]
It can also be written as,
\[3\overset{9}{\overline{\left){\begin{align}
& \,\,\,\,\,9 \\
& \underline{\,\,\,\,\,9\,\,\,\,} \\
& \underline{\,\,\,\,\,\times \,\,\,\,} \\
\end{align}}\right.}}\]
To understand the concept of Long division, let us take another example,
\[45\div 5=?\]
\[5\overset{9}{\overline{\left){\begin{align}
& \,\,\,\,\,45 \\
& \underline{\,\,\,\,\,45\,\,\,\,} \\
& \underline{\,\,\,\,\,\times \,\,\,\,\,\,\,} \\
\end{align}}\right.}}\]
Because \[5\times 9=45\]
Digit on the tens place is less than the divisor (4 < 5). Therefore, we will write quotient on ones. This is called Long Division.
IMPERFECT DIVISION
We have already learnt that division can be shown in two ways.
But sometimes, it doesn't work perfectly.
It happens whenever we get remainder in division. Let us, see what a remainder is.
There are 49 chocolates which have to be distributed amongst 9 friends. How many chocolates will each friend receive?
49 chocolates are to be shared equally amongst 9 friends. That is, \[49\div 9\]or
\[9\overline{\left){49}\right.}\]
An Interesting Poem on Division
Division, division, division
A terribly easy decision,
Let’s me just share,
My apple or pear,
With utter and perfect precision…
Here’s some good words of
advice,
I think I might say them all twice,
Learn each times tables,
And you’ll also be able,
To go and divide really nice…
Young laddie, it won’t make
Things worse,
Division brings no type of cruse,
Repeated subtraction?
Break to a fraction?
Or multiply things in reverse?
Quotients are things that we find,
When division’s how math
problem's signed,
It has the math smarts,
To cut pies in parts,
The inverse of things we
combined…
Historical Preview
In the book “How Mathematics Happened: The first 50, 000 years”, Peter Rudman said that the development of the concept of prime numbers could only have come about after the concept of division. Which he dates to after 10, 000 BC.
Sometimes in division, we may not be able to equally group or share the objects.
Something is left over.
This leftover number is called the remainder.
\[\begin{matrix}
\begin{matrix}
\text{Divisor}\leftarrow \overset{5\,\to }{\overline{\left){\begin{align}
& 49 \\
& \underline{45} \\
& 4 \\
\end{align}}\right.}} & \text{Quotient} \\
\end{matrix} & \to \,\operatorname{Remainder} \\
\end{matrix}\]
Let us have a look on another example:
\[451\div 6=?\]
| \[6\overset{75}{\overline{\left){\begin{align} & \,\,\,\,\,451 \\ & \underline{-\,42\downarrow } \\ & \,\,\,\,\,\,\,3\,\,1 \\ & \underline{-\,\,\,\,3\,0} \\ & 1 \\ \end{align}}\right.}}\] |
\[\left( 6\times 7=42 \right)\] \[\left( 45-42=3 \right)\] \[\left( 6\times 5=30 \right)\] \[\left( 31-30=1 \right)\] |
Here, Quotient = 75 & Remainder = 1
CHECKING THE ANSWERS
Let us check our answer of the above solved problem:
The trick is
\[\text{(Quotient }\!\!\times\!\!\text{ Divisor)+Remainder=Dividend}\]
So, on the left hand side we have,
Quotient = 75
Divisor = 6
Remainder =1
& on the right hand side we have
Dividend = 451
The answer would be correct if left hand side = Right hand side
Left hand side
\[(75\times 6)+1=450+1=451\]
Right hand side
451
Left hand side = Right hand side = 451
Therefore, our answer is correct.
DIVIDING A 4 DIGIT NUMBER
Dividing a 4 digit number is just like dividing any other 3 digit number.
A school has organized a medical camp for 6290 students of the school. The students were divided in groups of 5 students in each group. Let us find out how many such groups will be formed.
Number of groups formed = Total number of students – Number of students in 1 group
\[6290\div 5=?\]

Here, Quotient = 1258 & Remainder = 0
Therefore, the number of groups formed = 1258
Let us have a look on another example.
\[4853\div 2=?\]
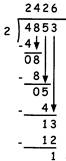
Here, Quotient = 2426 & Remainder = 1
DIVIDING A NUMBER BY 10
Let us find out \[891\div 10=\]______
To solve the above problem, we have an amazing shortcut. Let us have a look....
\[\overset{89}{\overline{\left){\begin{align}
& \,\,\,\,\,8\,\,9\,\,1 \\
& \underline{-8\,\,0\,\,\downarrow } \\
& \,\,\,\,\,\,\,\,\,9\,\,1 \\
& \underline{\,\,\,\,-9\,\,0} \\
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,1 \\
\end{align}}\right.}}\]
Misconcept/Concept
Misconcept: Division is commutative, order does not matter.
Concept: Division is not commutative, order does matter.

For example: \[891\div 10=?\]
Here, Quotient = 89 & Remainder = 1
Now,\[68\div 10=?\]
Quotient = 6 & Remainder = 8
\[590\div 10=?\]
Quotient = 59 & Remainder = 0
Isn't it easy?
DIVIDING A NUMBER BY A 2 DIGIT NUMBER
45 students were selected for presenting the school exhibition. They were divided in groups of 15 students in each group to assign different departments. Let us find out how many such groups were formed.
\[45\div 15=?\text{ or }15\overline{\left){45}\right.}\]
When we divide any number by any 2 digit number, first of all, we will estimate the quotient.
\[15\overline{\left){45}\right.}\]rounds to \[10\overline{\left){40}\right.}\]
To solve, this, \[10\times 4=40\]
Therefore, the quotient is 4.
Now, try this estimated quotient.
\[15\times 4=60>45\]
\[15\times 3=45=45\]
Finally,
\[15\overset{3}{\overline{\left){\begin{align}
& \,\,\,\,45 \\
& \underline{-45} \\
& \underline{\,\,\,\,\times \,\,}\,\, \\
\end{align}}\right.}}\]
Therefore, Quotient = 3 & Remainder = 0
A pastry shop made 310 pastries which are to be packed in 24 boxes. How many pastries will each box contain?
Total number, of  s = 310
s = 310
Total number of  s = 24
s = 24
Number of pastries in 1 box = Total number of pastries
Total number of boxes
\[=310\div 24\]
\[=24\overline{\left){310}\right.}\]
Here we have to divide the number by a 2 digit number.
Therefore, we will estimate the quotient first.
\[24\overline{\left){310}\right.}\]rounds to \[20\overline{\left){300}\right.}\]
To solve this, \[20\times 15=300\]
Therefore, the quotient is 15.
Now, try this estimated quotient.
\[24\times 15=360>310\]
\[24\times 14=336>310\]
\[24\times 13=312>310\]
\[24\times 12=288<310\]
Finally.
\[24\overset{12}{\overline{\left){\begin{align}
& \,\,\,\,310 \\
& \underline{-288} \\
& \,\,\,\,\,\,\underline{22} \\
\end{align}}\right.}}\]
Therefore, Quotient = 12 & the Remainder = 22.
INTERESTING PATTERNS IN DIVISION
As the dividend increases, the quotient also increases.
\[4\div 2=2\]
\[40\div 20=20\]
\[400\div 200=200\]
\[4000\div 2000=2000\]
As the divisor increases, the quotient decreases.
\[4000\div 2=2000\]
\[4000\div 20=200\]
\[4000\div 200=20\]
\[4000\div 2000=2\]
You need to login to perform this action.
You will be redirected in
3 sec
