4th Class Mathematics Fractions Fractions

LEARNING OBJECTIVES

This lesson will help you to:—

• learn to identify half, one-fourth and three-fourth of a whole.
• learn and understand the meaning of 1/3, /4 and 2/3.
• learn to appreciate the equivalence of 2/4 and 1/2 and of 2/2, 3/3 and 4/4 and 1.
• study about the numerator and denominator of a fraction.
• learn about mixed fractions.
• study about addition and subtraction of fractions.

Real Life Examples

Sharing food is a good way to introduce various concepts about fractions. For example, using a chocolate bar and dividing it into pieces.

Measurements during baking uses fractions such as one fo0urth of a cup of milk or half a spoonful of sugar etc.

QUICK CONCEPT REVIEW

Whole Number: Whole Numbers are simply the numbers 0, 1, 2, 3, 4, 5... (and so on).They're not fractions, they are not decimals, they are simply whole numbers.

No Fractions!

Fraction: A fraction is a part of a whole.

Fraction= Numerator / Denominator.

TYPES OF FRACTION

There are three types of fraction:

• Proper Fraction: These are those fractions where numerator is smaller than the denominator.
• Improper Fraction: These are those fractions where numerator is larger than the denominator

Mixed Fractions

Numerator: The upper part of fraction that represents the number of parts you have.

Denominator: The lower part of fraction that represents the number of parts the whole is divided into.

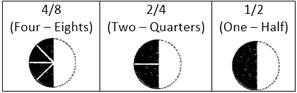
 Half (1/2)

• It is two parts of a whole.
• It has 1 as Numerator and 2 as Denominator.
• It is the simplest form.
• It is a proper fraction.

 One-Fourth (1/4)

• It is four parts of a whole.
• It has 1 as Numerator and 4 as Denominator.
• It is a proper fraction.

 Two-third (2/ 3)

• It is one part minus the whole.
• It is greater the 1/3 part.
• It is a proper fraction.
• It has 2 as Numerator and 3 as Denominator.

 Three-fourth (3/4)

• It is one fourth part minus the whole.
• It is greater than 1/4.
• It is a proper fraction.
• It has 3 as Numerator and 4 as Denominator.

Equivalence:

Some fractions may look different, but are really the same, for example:

• The equivalence is obtained by multiplying/dividing the numerator and denominator by a same number.
• 2/2 =3/3 =4/4 = 5/5= 6/6= 7/7......=1/1=1.

Amazing Facts

The word “fraction” originates from the Latin word, “fractus”, which means broken.

Only improper fractions can be converted into mixed numbers.

The bricks that were used to build the great bath Indus valley civilization were in perfect 4 : 2 : 1 ratio.

=1 + 3/4 = 1        3/4 = 7/4

Whole Number\[\text{2}\frac{\text{1}}{\text{3}}_{\text{Denominator}}^{\text{Narrator}}\]

Historical Preview

Fractions were firstly used in the Indus Valley civilization. Followed by the Egyptians and the Greeks.

The Egyptians wrote numbers (based on tens) alongside pictures called hieroglyphs.

For example: 1/3 + 1/5 would be represented as shown below:

Notice the man’s feet is pointing towards the direction of writing (from left to right). When the feet pointing toward the direction of writing means add. Otherwise, it means subtract. In this case, it is pointing towards the direction of writing.

Notice also that there is a shape that looks like an open mouth (the ellipse). It refers to a fraction.

Mixed Fractions

• A Mixed Fraction is a whole number and a proper fraction combined.

Ex. 1 2/3, 2 3/5 etc.

• For everyday use, people understand mixed fractions better: Example: It is easier to say "I ate 21/4 sausages", than "I ate 9/ 4 sausages".

CONVERTING IMPROPER FRACTIONS TO MIXED FRACTIONS

To convert an improper fraction to a mixed fraction, follow these steps:

1. Divide the numerator by the denominator.
2. Write down the whole number answer.
3. Then write down any remainder above the denominator.

Addition and Subtraction of Fractions

Addition/Subtraction when the denominator is same: You can add/subtract fractions easily if the bottom number (the denominator) is the same. Example:

       5/8     +          1/8     =         6/8     =         3/4

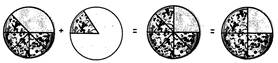
Addition/Subtraction when the denominator is different: When the denominator is not same, then we need to make the denominator same. The denominator can be made same by the following two methods:

• Common Denominator
• Least Common Denominator

Common Denominator: This method involves multiplying the given denominators together.

Example: 1/3 + 1/6 =?

Multiplying the current denominators 3 and 6 we get,\[3\times 6=18\]. Now instead of having 3 or 6 totals, we will have 18.

Thus, 6/18 + 3/18 = 9/18

Least Common Denominator: In the above example, 18 is a relatively larger number. Instead of using the common denominator way, we can also opt for least common denominator.

Here is how to find out;

1/3 List the multiples of 3: 3, 6, 9 , 12, 15, 18, 21.....

1/6 List the multiples of 6: 6, 12, 18, 24, 30, 36......

Then find the smallest number that is the same. The answer is 6, and that is the least common denominator.

• When we multiply top and bottom of 1/3 by 2 we get 2/6
• 1/6 already has g denominator of 6

The question now looks like:

2/6 +176 = 3/6

• Last step is to simplify the fraction (if possible). In this case 3/6 is simpler as 1/ 2.

Thus the steps followed are:

1. Find the least common multiple of the denominators (which is called the Least Common Denominator).
2. Change each fraction (using equivalent fractions) to make their denominators the same as the least common denominator.
3. Then add (or subtract) the fractions.

MULTIPLICATION OF FRACTIONS

There are 3 simple steps to multiply fractions

1. Multiply the top numbers (the numerators).
2. Multiply the bottom numbers (the denominators).
3. Simplify the fraction if needed.

DIVISION OF FRACTIONS

There, are 3 simple steps to divide fractions;

1. Turn the second fraction (the one you want to divide by) upside-down (this is now a reciprocal).
2. Multiply the first fraction by that reciprocal.
3. Simplify the fraction (if needed).

Misconcept/Concept

Misconcept: The fractions with numerator other than 1 are greater than 1.

Concept: You can’t have a fraction that is bigger than one.

Misconcept: The bigger the number on the bottom, the bigger the fraction.

Concept: This is not true. The smaller the number on the denominator, the bigger will be the fraction. For example: 1/2 is bigger than 1/6.