4th Class Mathematics Fun with Numbers-973 Number series

    Number series

 

 

Around us, there are different kinds of things. They are in the form of clothes, wrapping papers, carpets and many more. A pattern of the things can be in different shapes or design repeated in a particular way. For example, look at the series of shapes given below:  

 

 

 

There are four groups of picture shown above and each group has circles and squares in this way the first group has one square and one circle, second has two squares and one circle, third has two square and two circles, and fourth has three squares and two circles. Therefore, according to the above pattern the fifth group of the following pattern will have three squares and three circles. Numbers can also be in patterns as given below:                  

 

 

2, 4, 6, 8, 10, 12, 14, 16, 18, 20, _ _ _ _ _ _ _ _ _ .

The system or the relation between the consecutive numbers is very simple, adding 2 to a number gives the next number. In this chapter, we will see many more system of relation of numbers.  

 

System Charts and Tables of Numbers

 

Row                                              Column

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100

 

This is a number chart of the first 100 counting numbers. The numbers are arranged in 10 rows and 10 columns.  

 

There are many systems in the chart. Some of them are given below. 

• The numbers in each row increase by 1, and the numbers in each column increase by 10.
• All the numbers in the first column end with digit 1, all the numbers in the second column end with digit 2, and so on.
• The number in the first column, third column, fifth column, and so on, are odd numbers.
• The numbers in the second column, fourth column, sixth column, and so on, are even numbers.
• The numbers in the fifth and tenth columns are multiples of 5.
• The numbers in the last column are multiples of 10.    

 

In the following table, counting numbers from 1 to 36 are arranged in 6 rows and 6 columns:

1	2	3	4	5	6
7	8	9	10	11	12
13	14	15	16	17	18
19	20	21	22	23	24
25	26	27	28	29	30
31	32	33	34	35	36

                   The relation between the numbers shown above are given below:  

1	2	3	4	5	6
7	8	9	10	11	12
13	14	15	16	17	18
19	20	21	22	23	24
25	26	27	28	29	30
31	32	33	34	35	36

                    Multiple of 2, increasing by 6 as we move down:  

1	2	3	4	5	6
7	8	9	10	11	12
13	14	15	16	17	18
19	20	21	22	23	24
25	26	27	28	29	30
31	32	33	34	35	36

                    Multiple of 3, increasing by 6 as we move down  

1	2	3	4	5	6
7	8	9	10	11	12
13	14	15	16	17	18
19	20	21	22	23	24
25	26	27	28	29	30
31	32	33	34	35	36

                    Multiple of 5  

1	2	3	4	5	6
7	8	9	10	11	12
13	14	15	16	17	18
19	20	21	22	23	24
25	26	27	28	29	30
31	32	33	34	35	36

                   

                    Multiple of 7  

 

 System of Addition of Numbers

See the pattern of the addition of consecutive numbers starting from 1:

\[1+2=3=(2\times 3)\div 2\] 

\[1+2+3=6=(3\times 4)\div 2\]

 \[1+2+3+4+5=15=(5\times 6)\div 2\] 

We can see, the sum of consecutive numbers starting from 1. = (last number x next number)\[\div 2\]   

Now, find the sum of the following numbers without using actual addition method.

\[1+2+3+4+5+6+7+8+9+10=(10\times 11)\div 2=55\]

\[1+2+3+4+5+6+7+8+9+10+11+12+13=(13+14)\div 2=91\]

See the pattern of the addition of the consecutive odd numbers starting from 1:

\[1+3=4=2\times 2\]

\[1+3+5=9=3\times 3\] 

\[1+3+5+7=16=4\times 4\]

\[1+3+5+7+9=25=5\times 5\]  

As we can see, the sum of consecutive odd numbers from 1 depends on how many odd numbers are added in the pattern. Thus, if there are 6 consecutive odd numbers starting from 1, their sum will be \[6\times 6=36\]. Now do the following sums without using actual addition:

 

\[1+3+5+7+9+11+13+15+17+19=(10\times 10)=100\]

\[1+3+5+7+9+11+13+15+17+19+21+23+25+27=(14\times 14)=196\]   

Observe the following Pattern Carefully:

\[\left( 2\times 2 \right)-\left( 1\times 1 \right)=4-1=3=2+1\]

\[\left( 3\times 3 \right)-\left( 2\times 2 \right)=9-4=5=3+2\] 

\[\left( 4\times 4 \right)-\left( 3\times 3 \right)=16-9=7=4+3\] 

\[\left( 5\times 5 \right)-\left( 4\times 4 \right)=25-16=9=5+4\] 

\[\left( 8\times 8 \right)-\left( 7\times 7 \right)=64-49=15=8+7\] 

\[\left( 11\times 11 \right)-\left( 10\times 10 \right)=121-100=21=11+10\]    

 

• System of Multiplication:

\[1\times 11=11\] 

\[11\times 11=121\] 

\[111\times 11=1221\]   

\[1111\times 11=12221\]

 

• System of Division

Observe the given pattern carefully:

\[111\div 3=37\]

\[222\div 6=37\]

\[333\div 9=37\]

\[444\div 11=37\] 

In the above pattern, dividend are product of 37 and four consecutive multiples of three.  

 

• System of Numbers Arranged in a Shape:

 

 

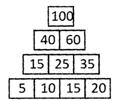
Numbers can be arranged to form a shape or fit inside a shape. These numbers can also have a pattern. Here, some numbers are arranged as a pyramid.

Look at the two consecutive numbers in the fourth row (from top) and from the number above. We find that:

5 + 10 =15                              10 + 15 = 25                                   15 + 20 = 35

Look at the two consecutive numbers in the third row and from the number above, we find that,

15 + 25 = 40                         25 + 35 = 60                                    Finally,  40 + 60 = 100  

Using the same pattern, complete the following number pyramid:

 

 

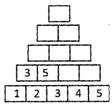
The number pyramid should look like,

 

 

 

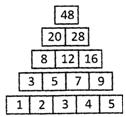
Study the pattern and fill in the blanks with the suitable number?

2, 4, __________ , 8, 10, 12, etc.

 

Solution:

Each number in the pattern is 2 greater than previous number.  

2 + 2 = 4, 4 + 2 = 6, 6 + 2 = 8, 8 + 2 = 10, 10 + 2 =12,  etc.    

 

 

 

• Number are mathematical objects by which we express date, time position, quantity, etc.
• Both the system of numeration (Indian and international) is based on 10.
• Successor of a number is one more than the number.
• When numbers are arranged the increasing order, the order is called ascending order.
• When numbers are arranged in decreasing order, the order is called descending order.
• When numbers or figures are arranged in a specific way, it is called pattern.    

 

 

 

• Hindu Arabic numeral was introduced to the Europe by the Italian mathematician Leonardo pisano.
• The modern symbols 1,2,3,4,5,6,7,8,9 have been evolved from the Brahmi numerals.      

 

 

  

 

 What is missing number in the square?

 

 

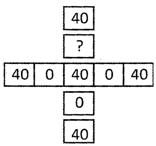
(a) 0                                                      

(b) 10

(c) 40                                                    

(d) 20

(e) None of these

 

Answers (a)

Explanation

40  + 0 = 40  

 

 

 Fill in the blanks 4, 8,12,16, __,___?

(a) 20,24                                              

(b) 24,28

(c) 28,30                                              

(d) 32,34

(e) None of these

 

Answers (a)

Explanations

In the given pattern, each number is greater by 4 than the pervious number. Therefore, option (a) is correct.  

 

 

 What is missing number in the square?

 

 

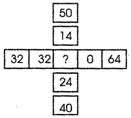
(a) 64                                                    

(b) 53

(c) 50                                                    

(d) 48

(e) 15

 

Answers (a)

Explanations

50 +14 = 64,  64 + 0 = 64, 32 + 32 = 64, 40 + 24 = 64  

 

 

The digit at ten millions place in the number 548745896545 is

(a) 5                                                      

(b) 6

(c) 4                                                      

(d) 7

(e) None of these

 

Answers (c)  

 

 

 Find difference between the greatest and smallest numbers formed by the digits 7, 9, 5, 4, 8, 2, 1, 3, 0 without repeating the digit?

(a) 885,197,421                                 

(b) 885,917,421

(c) 865,197,421                                 

(d) 845,197,421

(e) None of these

 

Answers (a)