LEARNING OBJECTIVES
This lesson will help you to:—
- understand two dimensional and three dimensional geometrical figures.
- learn about line symmetry, symmetrical and asymmetrical shapes.
- determine the number of line of symmetry.
- identify the different types of triangles on the basis of sides and angles.
- understand the different kinds of angles.
- learn about the angle sum properties of triangle and quadrilateral.
- Know about the terms related to the circle.
QUICK CONCEPT REVIEW
Circle
- A circle is a closed figure formed by points equidistant from a fixed point.
- Every circle has a fixed centre.
- The perimeter of the circle is called its circumference
- The distance between the centre and any point on the circle is called its radius.
A line segment passing through the centre of the circle, whose end points lie on the circle is called the diameter of the circle.
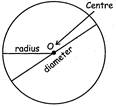
- The diameter of a circle is twice the radius.
- A line segment whose end points lie on the circle is called a chord.
- The diameter is the longest chord of a circle.
- Any part of a circle is called an arc.
- If an arc represents half of the circle it is a semicircle.
ANGLE
Two rays with a common end point form an angle. It is denoted by\[\angle \].
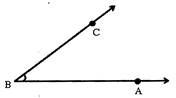
- The common end point is known as the vertex of the angle.
- The rays forming an angle are called the arms or sides of the angle.
- Angles measures in degrees.
- An angle whose measure is between\[{{0}^{o}}\]and\[{{90}^{o}}\]is called an acute angle.
- An angle whose measure is\[{{90}^{o}}\]is called a right angle.
- An angle whose measure is more than\[{{90}^{o}}\]but less than\[{{180}^{o}}\]is called an obtuse angle.
- An angle whose measure is\[{{180}^{o}}\]is called a straight angle and whose measure is\[{{360}^{o}}\]is called whole angle.
- An angle whose measure is more than\[{{180}^{o}}\]but less than\[{{360}^{o}}\]is called a reflex angle.
A TRIANGLE
- A triangle is a closed figure having three sides, three vertices and three angles. It is denoted by\[\Delta \].
- Triangles can be classified on the basis of their sides and angles.
- Triangle in which all sides are equal is called equilateral
- Triangle in which two sides are equal is called isosceles
- Triangle in which all the three sides are different is called scalene
- Right angled Triangle:-
In this, only one angle is of \[{{90}^{o}}\]
- A cute - angled triangle:-
- All angles of this triangle are acute.
- Obtuse - angled triangle:-
- In this triangle, at least one angle is an obtuse angle.
- The sum of 3 angles of a triangle is\[{{180}^{o}}\].
A QUADRILATERAL
- A quadrilateral is a four - sided closed figure. It has four vertices, and four angles.
- The sum of four angles of a quadrilateral is\[{{360}^{o}}\].
- Square, Rectangle, parallelograms etc. are examples of quadrilateral.
SYMMETRY
- Symmetrical shapes can be folded into two matching equal halves
- The place from where symmetrical shapes are folded is called the line of symmetry.
- A symmetrical shapes cannot be folded into two equal halves.
- A symmetrical shapes do not have a line of symmetry.
- The line of symmetry is also known as mirror line or line of reflection.
- If a figure can be folded such that one part of it exactly matches with the other then the figure has a line of symmetry.
- A square has four lines of symmetry, rectangle has two lines of symmetry and a triangle (whose 3 sides are equal) has 3 lines of symmetry
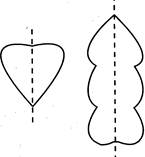
- Some figures have only one line of symmetry. Eg.
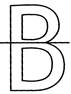
- Some figures have no line of symmetry for e.g.
TESSELLATIONS
- We can fit some shapes of tiles such that there are no gaps and they do not overlap. These tilings ore called tessellations.

Tessellating shape

Shape that does not tessellate




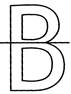
![]()
![]()


